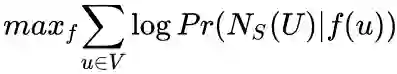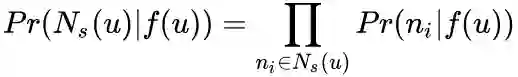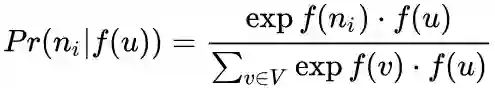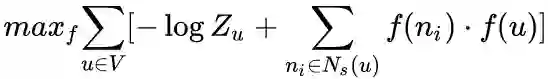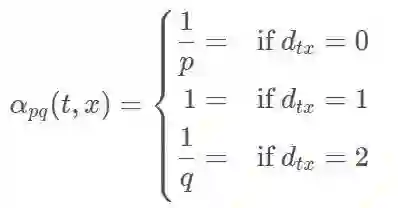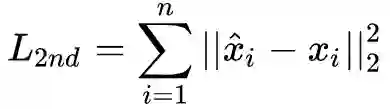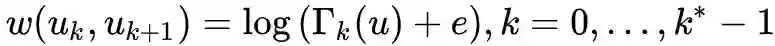Graph Embedding 图表示学习的原理及应用

文章作者:浅梦
导读:我们都知道在数据结构中,图是一种基础且常用的结构。现实世界中许多场景可以抽象为一种图结构,如社交网络,交通网络,电商网站中用户与物品的关系等。
目前提到图算法一般指:
经典数据结构与算法层面的:最小生成树 (Prim,Kruskal,...) ,最短路 (Dijkstra,Floyed,...) ,拓扑排序,关键路径等
概率图模型,涉及图的表示,推断和学习,详细可以参考 Koller 的书或者公开课
图神经网络,主要包括 Graph Embedding (基于随机游走)和 Graph CNN (基于邻居汇聚)两部分。
这里先看下 Graph Embedding 的相关内容。
Graph Embedding 技术将图中的节点以低维稠密向量的形式进行表达,要求在原始图中相似 ( 不同的方法对相似的定义不同 ) 的节点其在低维表达空间也接近。得到的表达向量可以用来进行下游任务,如节点分类,链接预测,可视化或重构原始图等。
01
DeepWalk
虽然 DeepWalk 是 KDD 2014的工作,但却是我们了解 Graph Embedding 无法绕过的一个方法。
我们都知道在 NLP 任务中,word2vec 是一种常用的 word embedding 方法, word2vec 通过语料库中的句子序列来描述词与词的共现关系,进而学习到词语的向量表示。
DeepWalk 的思想类似 word2vec,使用图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系,DeepWalk 给出的方法是使用随机游走 (RandomWalk) 的方式在图中进行节点采样。
RandomWalk 是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
获取足够数量的节点访问序列后,使用 skip-gram model 进行向量学习。
DeepWalk 核心代码
DeepWalk 算法主要包括两个步骤,第一步为随机游走采样节点序列,第二步为使用 skip-gram modelword2vec 学习表达向量。
构建同构网络,从网络中的每个节点开始分别进行 Random Walk 采样,得到局部相关联的训练数据
对采样数据进行 SkipGram 训练,将离散的网络节点表示成向量化,最大化节点共现,使用 Hierarchical Softmax 来做超大规模分类的分类器
Random Walk
我们可以通过并行的方式加速路径采样,在采用多进程进行加速时,相比于开一个进程池让每次外层循环启动一个进程,我们采用固定为每个进程分配指定数量的num_walks的方式,这样可以最大限度减少进程频繁创建与销毁的时间开销。
deepwalk_walk方法对应上一节伪代码中第6行,_simulate_walks对应伪代码中第3行开始的外层循环。最后的Parallel为多进程并行时的任务分配操作。
def deepwalk_walk(self, walk_length, start_node):
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(self.G.neighbors(cur))
if len(cur_nbrs) > 0:
walk.append(random.choice(cur_nbrs))
else:
break
return walk
def _simulate_walks(self, nodes, num_walks, walk_length,):
walks = []
for _ in range(num_walks):
random.shuffle(nodes)
for v in nodes:
walks.append(self.deepwalk_walk(alk_length=walk_length, start_node=v))
return walks
results = Parallel(n_jobs=workers, verbose=verbose, )(
delayed(self._simulate_walks)(nodes, num, walk_length) for num in
partition_num(num_walks, workers))
walks = list(itertools.chain(*results))Word2vec
这里就偷个懒直接用gensim里的 Word2Vec 了。
from gensim.models import Word2Vec
w2v_model = Word2Vec(walks,sg=1,hs=1)DeepWalk 应用
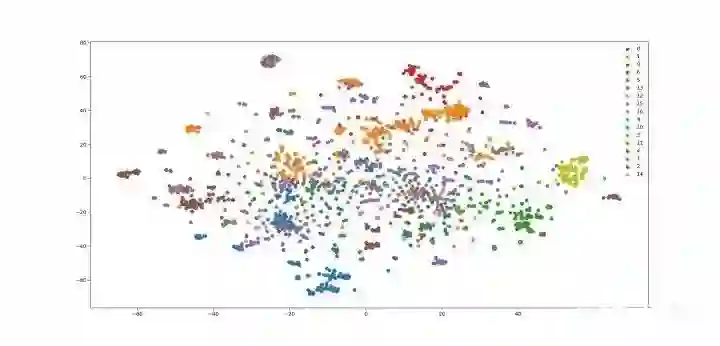
这里简单的用 DeepWalk 算法在 wiki 数据集上进行节点分类任务和可视化任务。 wiki 数据集包含 2,405 个网页和17,981条网页之间的链接关系,以及每个网页的所属类别。
本例中的训练,评测和可视化的完整代码在下面的 git 仓库中:
https://github.com/shenweichen/GraphEmbedding
G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])
model = DeepWalk(G,walk_length=10,num_walks=80,workers=1)
model.train(window_size=5,iter=3)
embeddings = model.get_embeddings()
evaluate_embeddings(embeddings)
plot_embeddings(embeddings)分类任务结果
micro-F1 : 0.6674
macro-F1 : 0.5768
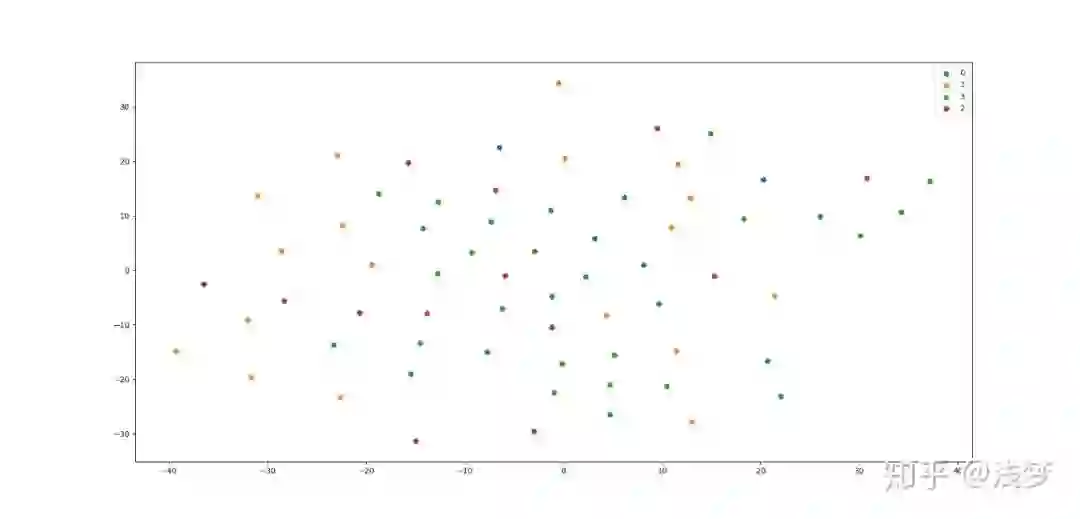
可视化结果
之前介绍过DeepWalk,DeepWalk使用DFS随机游走在图中进行节点采样,使用word2vec在采样的序列学习图中节点的向量表示。
LINE也是一种基于邻域相似假设的方法,只不过与DeepWalk使用DFS构造邻域不同的是,LINE可以看作是一种使用BFS构造邻域的算法。此外,LINE还可以应用在带权图中(DeepWalk仅能用于无权图)。
之前还提到不同的graph embedding方法的一个主要区别是对图中顶点之间的相似度的定义不同,所以先看一下LINE对于相似度的定义。
LINE 算法原理
1. 一种新的相似度定义
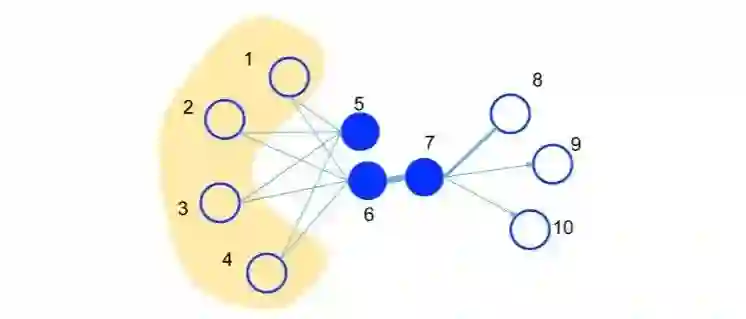
first-order proximity
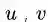 之间存在直连边,则边权
之间存在直连边,则边权
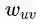 即为两个顶点的相似度,若不存在直连边,则1阶相似度为0。如上图,6和7之间存在直连边,且边权较大,则认为两者相似且1阶相似度较高,而5和6之间不存在直连边,则两者间1阶相似度为0。
即为两个顶点的相似度,若不存在直连边,则1阶相似度为0。如上图,6和7之间存在直连边,且边权较大,则认为两者相似且1阶相似度较高,而5和6之间不存在直连边,则两者间1阶相似度为0。
second-order proximity
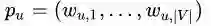 表示顶点
表示顶点
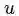 与所有其他顶点间的1阶相似度,则
与所有其他顶点间的1阶相似度,则
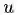 与
与
 的2阶相似度可以通过
的2阶相似度可以通过
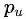 和
和
 的相似度表示。若
的相似度表示。若
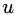 与
与
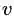 之间不存在相同的邻居顶点,则2阶相似度为0。
之间不存在相同的邻居顶点,则2阶相似度为0。
2. 优化目标
1st-order
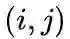 ,定义顶点
,定义顶点
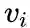 和
和
 之间的联合概率为:
之间的联合概率为:
 ,
,
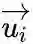 为顶点
为顶点
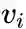 的低维向量表示。(可以看作一个内积模型,计算两个item之间的匹配程度)
的低维向量表示。(可以看作一个内积模型,计算两个item之间的匹配程度)
 ,
,
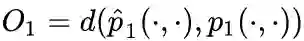
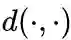 是两个分布的距离,常用的衡量两个概率分布差异的指标为KL散度,使用KL散度并忽略常数项后有:
是两个分布的距离,常用的衡量两个概率分布差异的指标为KL散度,使用KL散度并忽略常数项后有:

2nd-order
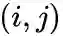 ,定义给定顶点
,定义给定顶点
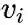 条件下,产生上下文(邻居)顶点
条件下,产生上下文(邻居)顶点
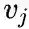 的概率为:
的概率为:
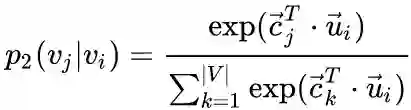 ,其中
,其中
 为上下文顶点的个数。
为上下文顶点的个数。
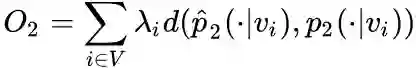 ,其中
,其中
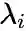 为控制节点重要性的因子,可以通过顶点的度数或者PageRank等方法估计得到。
为控制节点重要性的因子,可以通过顶点的度数或者PageRank等方法估计得到。
 ,
,
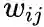 是边
是边
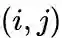 的边权,
的边权,
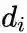 是顶点
是顶点
 的出度,对于带权图,
的出度,对于带权图,
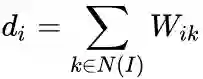 使用KL散度并设
使用KL散度并设
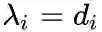 ,忽略常数项,有
,忽略常数项,有
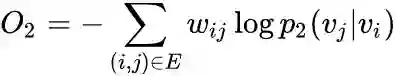
3. 优化技巧
Negative sampling
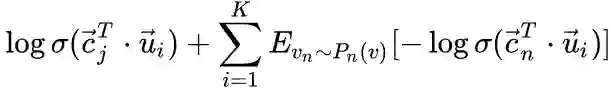 ,
,
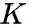 是负边的个数。
是负边的个数。
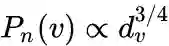 ,
,
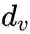 是顶点
是顶点
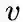 的出度。
的出度。
Edge Sampling
 ,在使用梯度下降方法优化参数时,
,在使用梯度下降方法优化参数时,
 会直接乘在梯度上。如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度过小。
会直接乘在梯度上。如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度过小。
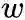 的边,则拆分后为
的边,则拆分后为
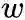 个权重为1的边。这样可以解决学习率选择的问题,但是由于边数的增长,存储的需求也会增加。
个权重为1的边。这样可以解决学习率选择的问题,但是由于边数的增长,存储的需求也会增加。
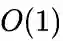 时间复杂度的离散事件抽样算法。具体内容可以参考
时间复杂度的离散事件抽样算法。具体内容可以参考
Alias Method:时间复杂度O(1)的离散采样方法
新加入顶点
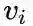 ,若该顶点与图中顶点存在边相连,我们只需要固定模型的其他参数,优化如下两个目标之一即可:
,若该顶点与图中顶点存在边相连,我们只需要固定模型的其他参数,优化如下两个目标之一即可:
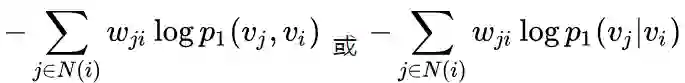
LINE核心代码
1. 模型和损失函数定义
order
控制是分开优化还是联合优化,论文推荐分开优化。
label
定义为1或者-1,通过模型输出的内积和
line_loss
就可以优化使用了负采样技巧的目标函数了~
def line_loss(y_true, y_pred):
return -K.mean(K.log(K.sigmoid(y_true*y_pred)))def create_model(numNodes, embedding_size, order='second'):
v_i = Input(shape=(1,))
v_j = Input(shape=(1,))
first_emb = Embedding(numNodes, embedding_size, name='first_emb')
second_emb = Embedding(numNodes, embedding_size, name='second_emb')
context_emb = Embedding(numNodes, embedding_size, name='context_emb')
v_i_emb = first_emb(v_i)
v_j_emb = first_emb(v_j)
v_i_emb_second = second_emb(v_i)
v_j_context_emb = context_emb(v_j)
first = Lambda(lambda x: tf.reduce_sum(
x[0]*x[1], axis=-1, keep_dims=False), name='first_order')([v_i_emb, v_j_emb])
second = Lambda(lambda x: tf.reduce_sum(
x[0]*x[1], axis=-1, keep_dims=False), name='second_order')([v_i_emb_second, v_j_context_emb])
if order == 'first':
output_list = [first]
elif order == 'second':
output_list = [second]
else:
output_list = [first, second]
model = Model(inputs=[v_i, v_j], outputs=output_list)2. 顶点负采样和边采样
下面的函数功能是创建顶点负采样和边采样需要的采样表。中规中矩,主要就是做一些预处理,然后创建alias算法需要的两个表。
def _gen_sampling_table(self):
# create sampling table for vertex
power = 0.75
numNodes = self.node_size
node_degree = np.zeros(numNodes) # out degree
node2idx = self.node2idx
for edge in self.graph.edges():
node_degree[node2idx[edge[0]]
] += self.graph[edge[0]][edge[1]].get('weight', 1.0)
total_sum = sum([math.pow(node_degree[i], power)
for i in range(numNodes)])
norm_prob = [float(math.pow(node_degree[j], power)) /
total_sum for j in range(numNodes)]
self.node_accept, self.node_alias = create_alias_table(norm_prob)
# create sampling table for edge
numEdges = self.graph.number_of_edges()
total_sum = sum([self.graph[edge[0]][edge[1]].get('weight', 1.0)
for edge in self.graph.edges()])
norm_prob = [self.graph[edge[0]][edge[1]].get('weight', 1.0) *
numEdges / total_sum for edge in self.graph.edges()]
self.edge_accept, self.edge_alias = create_alias_table(norm_prob)LINE 应用
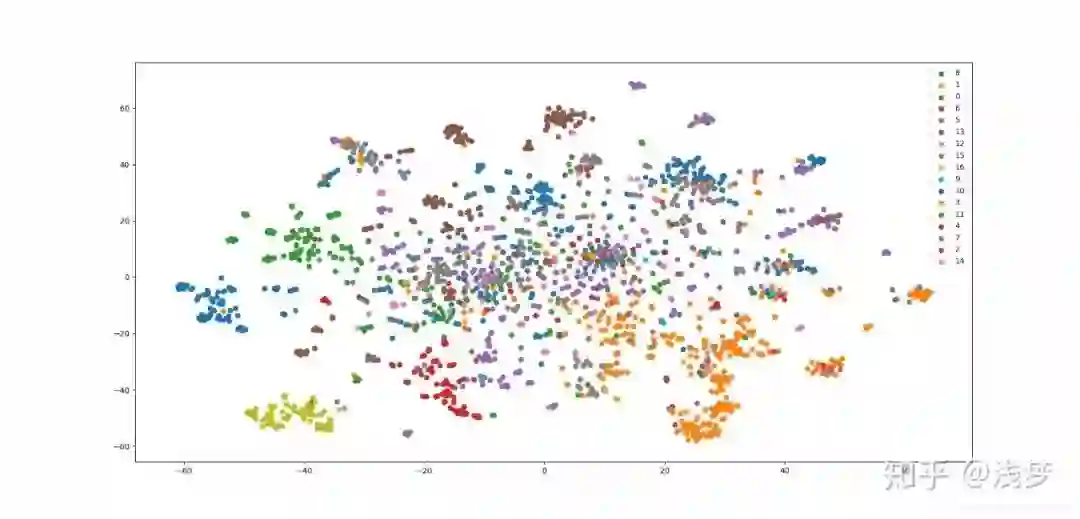
和之前一样,还是用LINE在wiki数据集上进行节点分类任务和可视化任务。wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系,以及每个网页的所属类别。由于1阶相似度仅能应用于无向图中,所以本例中仅使用2阶相似度。
本例中的训练,评测和可视化的完整代码在下面的git仓库中,
https://github.com/shenweichen/GraphEmbedding
G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])
model = LINE(G,embedding_size=128,order='second')
model.train(batch_size=1024,epochs=50,verbose=2)
embeddings = model.get_embeddings()
evaluate_embeddings(embeddings)
plot_embeddings(embeddings)分类任务结果
micro-F1: 0.6403
macro-F1:0.5286
结果有一定随机性,可以多运行几次,或者稍微调整epoch个数。
可视化结果
nodo2vec
前面介绍过基于DFS邻域的DeepWalk和基于BFS邻域的LINE。
node2vec是一种综合考虑DFS邻域和BFS邻域的graph embedding方法。简单来说,可以看作是deepwalk的一种扩展,是结合了DFS和BFS随机游走的deepwalk。
nodo2vec 算法原理
1. 优化目标
设 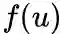
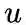

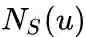


node2vec优化的目标是给定每个顶点条件下,令其近邻顶点(如何定义近邻顶点很重要)出现的概率最大。
为了将上述最优化问题可解,文章提出两个假设:
条件独立性假设
假设给定源顶点下,其近邻顶点出现的概率与近邻集合中其余顶点无关。
特征空间对称性假设
这里是说一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。(对比LINE中的2阶相似度,一个顶点作为源点和近邻点的时候是拥有不同的embedding向量的) 在这个假设下,上述条件概率公式可表示为:
根据以上两个假设条件,最终的目标函数表示为:
由于归一化因子:
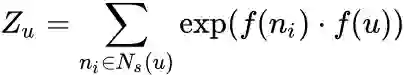
2. 顶点序列采样策略
node2vec依然采用随机游走的方式获取顶点的近邻序列,不同的是node2vec采用的是一种有偏的随机游走。
给定当前顶点 

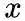
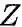
node2vec引入两个超参数 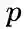
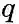
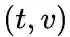
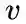
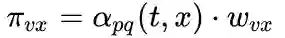
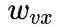
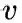
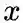
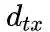


下面讨论超参数p和 q对游走策略的影响
Return parameter,p
参数p控制重复访问刚刚访问过的顶点的概率。注意到p仅作用于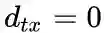

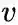
In-out papameter,q
q控制着游走是向外还是向内,若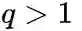
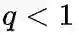
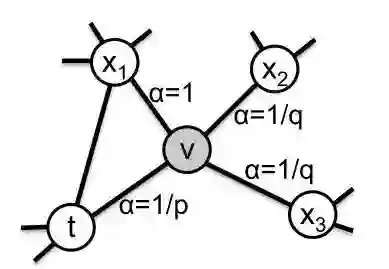
下面的图描述的是当从t访问到
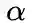
3. 学习算法
采样完顶点序列后,剩下的步骤就和deepwalk一样了,用word2vec去学习顶点的embedding向量。值得注意的是node2vecWalk中不再是随机抽取邻接点,而是按概率抽取,node2vec采用了Alias算法进行顶点采样。
Alias Method:时间复杂度O(1)的离散采样方法
https://zhuanlan.zhihu.com/p/54867139
node2vec 核心代码
1. node2vecWalk
通过上面的伪代码可以看到,node2vec和deepwalk非常类似,主要区别在于顶点序列的采样策略不同,所以这里我们主要关注node2vecWalk的实现。
由于采样时需要考虑前面2步访问过的顶点,所以当访问序列中只有1个顶点时,直接使用当前顶点和邻居顶点之间的边权作为采样依据。当序列多余2个顶点时,使用文章提到的有偏采样。
def node2vec_walk(self, walk_length, start_node):
G = self.G
alias_nodes = self.alias_nodes
alias_edges = self.alias_edges
walk = [start_node]
while len(walk) < walk_length:
cur = walk[-1]
cur_nbrs = list(G.neighbors(cur))
if len(cur_nbrs) > 0:
if len(walk) == 1:
walk.append(cur_nbrs[alias_sample(alias_nodes[cur][0], alias_nodes[cur][1])])
else:
prev = walk[-2]
edge = (prev, cur)
next_node = cur_nbrs[alias_sample(alias_edges[edge][0],alias_edges[edge][1])]
walk.append(next_node)
else:
break
return walk2. 构造采样表
preprocess_transition_probs
分别生成
alias_nodes
和
alias_edges
,
alias_nodes
存储着在每个顶点时决定下一次访问其邻接点时需要的alias表(不考虑当前顶点之前访问的顶点)。
alias_edges
存储着在前一个访问顶点为t,当前顶点为
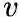 时决定下一次访问哪个邻接点时需要的alias表。
时决定下一次访问哪个邻接点时需要的alias表。
get_alias_edge
方法返回的是在上一次访问顶点 t,当前访问顶点为
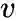 时到下一个顶点
时到下一个顶点
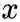 的未归一化转移概率:
的未归一化转移概率:

def get_alias_edge(self, t, v):
G = self.G
p = self.p
q = self.q
unnormalized_probs = []
for x in G.neighbors(v):
weight = G[v][x].get('weight', 1.0)# w_vx
if x == t:# d_tx == 0
unnormalized_probs.append(weight/p)
elif G.has_edge(x, t):# d_tx == 1
unnormalized_probs.append(weight)
else:# d_tx == 2
unnormalized_probs.append(weight/q)
norm_const = sum(unnormalized_probs)
normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]
return create_alias_table(normalized_probs)def preprocess_transition_probs(self):
G = self.G
alias_nodes = {}
for node in G.nodes():
unnormalized_probs = [G[node][nbr].get('weight', 1.0) for nbr in G.neighbors(node)]
norm_const = sum(unnormalized_probs)
normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]
alias_nodes[node] = create_alias_table(normalized_probs)
alias_edges = {}
for edge in G.edges():
alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
self.alias_nodes = alias_nodes
self.alias_edges = alias_edges
returnnode2vec 应用
使用node2vec在wiki数据集上进行节点分类任务和可视化任务。wiki数据集包含 2,405 个网页和17,981条网页之间的链接关系,以及每个网页的所属类别。通过简单的超参搜索,这里使用p=0.25,q=4的设置。
本例中的训练,评测和可视化的完整代码在下面的git仓库中:
https://github.com/shenweichen/GraphEmbedding
G = nx.read_edgelist('../data/wiki/Wiki_edgelist.txt',create_using=nx.DiGraph(),nodetype=None,data=[('weight',int)])
model = Node2Vec(G,walk_length=10,num_walks=80,p=0.25,q=4,workers=1)
model.train(window_size=5,iter=3)
embeddings = model.get_embeddings()
evaluate_embeddings(embeddings)
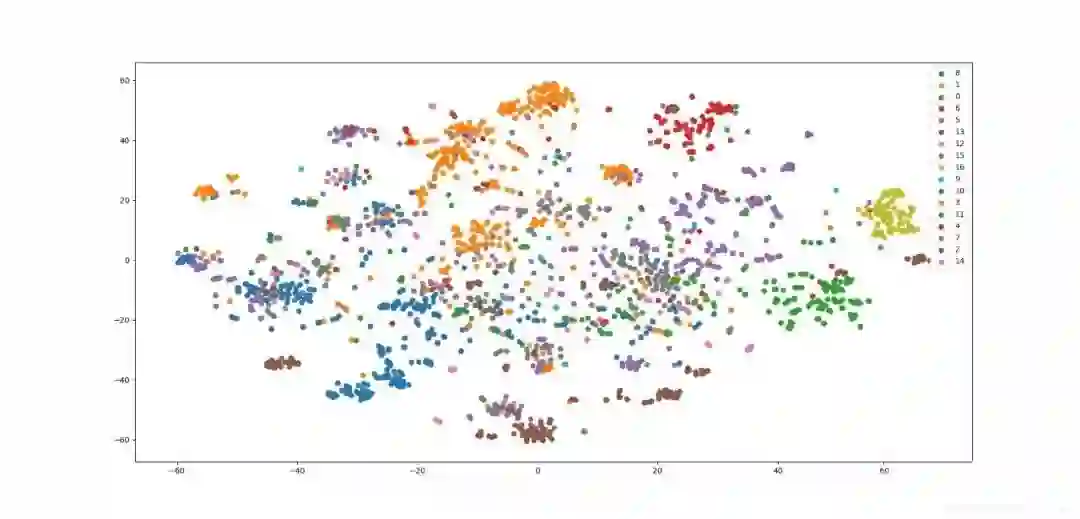
plot_embeddings(embeddings)分类任务
可视化
当机器学习遇上复杂网络:解析微信朋友圈 Lookalike 算法
SDNE 算法原理
相似度定义
2阶相似度优化目标
 个顶点,有
个顶点,有
 ,每一个
,每一个
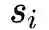 都包含了顶点i的邻居结构信息,所以这样的重构过程能够使得结构相似的顶点具有相似的embedding表示向量。
都包含了顶点i的邻居结构信息,所以这样的重构过程能够使得结构相似的顶点具有相似的embedding表示向量。
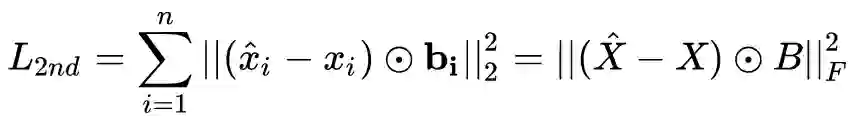
 为逐元素积,
为逐元素积,
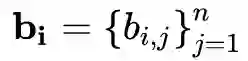 ,若
,若
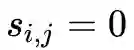 ,则
,则
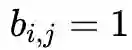 ,否则
,否则

1阶相似度优化目标
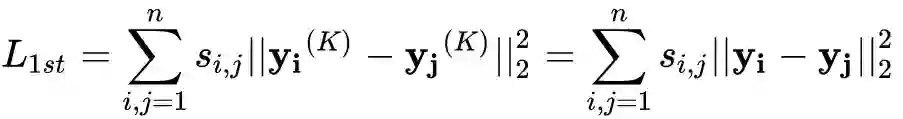
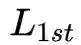 还可以表示为
还可以表示为
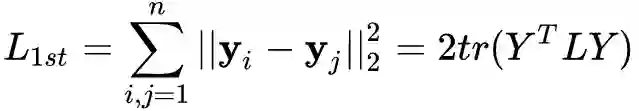
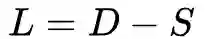 ,D是图中顶点的度矩阵,S是邻接矩阵,
,D是图中顶点的度矩阵,S是邻接矩阵,
 。
。
整体优化目标
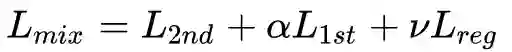
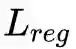 是正则化项,
是正则化项,
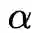 为控制1阶损失的参数,
为控制1阶损失的参数,
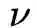 为控制正则化项的参数。
为控制正则化项的参数。
模型结构
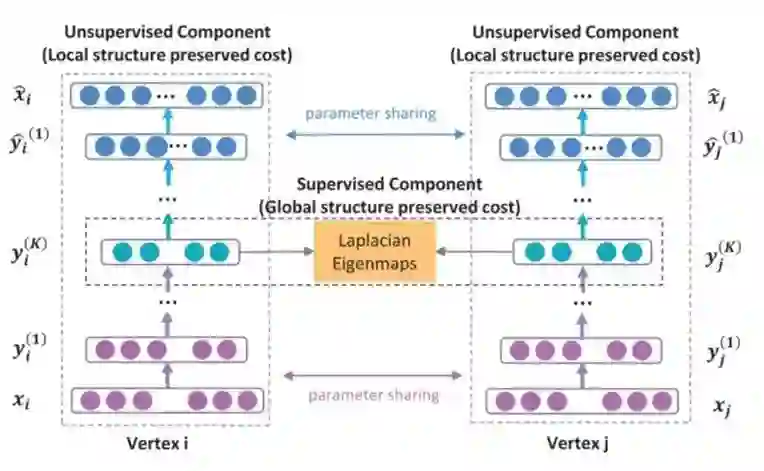
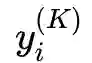 就是我们需要的embedding向量,模型通过1阶损失函数使得邻接的顶点对应的embedding向量接近,从而保留顶点的局部结构特性(中间应该是 Local structure preserved cost)
就是我们需要的embedding向量,模型通过1阶损失函数使得邻接的顶点对应的embedding向量接近,从而保留顶点的局部结构特性(中间应该是 Local structure preserved cost)
实现
损失函数定义
l_2nd
是2阶相似度对应的损失函数,参数
beta
控制着非零元素的惩罚项系数。
y_true
和
y_pred
分别是输入的邻接矩阵和网络重构出的邻接矩阵。
l_1st
是1阶相似度对应的损失函数,参数
alpha
控制着其在整体损失函数中的占比。
def l_2nd(beta):
def loss_2nd(y_true, y_pred):
b_ = np.ones_like(y_true)
b_[y_true != 0] = beta
x = K.square((y_true - y_pred) * b_)
t = K.sum(x, axis=-1, )
return K.mean(t)
return loss_2nd
def l_1st(alpha):
def loss_1st(y_true, y_pred):
L = y_true
Y = y_pred
batch_size = tf.to_float(K.shape(L)[0])
return alpha * 2 * tf.linalg.trace(tf.matmul(tf.matmul(Y, L, transpose_a=True), Y)) / batch_size
return loss_1st
模型定义
create_model
函数创建SDNE模型,
l1
和
l2
分别为模型的正则化项系数,模型的输入
A
为邻接矩阵,
L
为拉普拉斯矩阵。输出
A_
为重构后的邻接矩阵,
Y
为顶点的embedding向量。
for
循环分别对应
encoder
和
decoder
结构。
def create_model(node_size, hidden_size=[256, 128], l1=1e-5, l2=1e-4):
A = Input(shape=(node_size,))
L = Input(shape=(None,))
fc = A
for i in range(len(hidden_size)):
if i == len(hidden_size) - 1:
fc = Dense(hidden_size[i], activation='relu',kernel_regularizer=l1_l2(l1, l2),name='1st')(fc)
else:
fc = Dense(hidden_size[i], activation='relu',kernel_regularizer=l1_l2(l1, l2))(fc)
Y = fc
for i in reversed(range(len(hidden_size) - 1)):
fc = Dense(hidden_size[i], activation='relu',kernel_regularizer=l1_l2(l1, l2))(fc)
A_ = Dense(node_size, 'relu', name='2nd')(fc)
model = Model(inputs=[A, L], outputs=[A_, Y])
return model
应用
可视化

阿里凑单算法首次公开!基于Graph Embedding的打包购商品挖掘系统解析
05
Struc2Vec
Struc2Vec算法原理
相似度定义
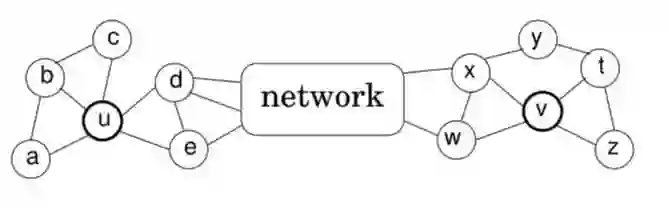
顶点对距离定义
 表示到顶点u距离为k的顶点集合,则
表示到顶点u距离为k的顶点集合,则
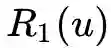 表示是u的直接相连近邻集合。
表示是u的直接相连近邻集合。
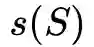 表示顶点集合S的有序度序列。
表示顶点集合S的有序度序列。
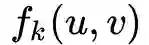 表示顶点u和v之间距离为k(这里的距离k实际上是指距离小于等于k的节点集合)的环路上的结构距离(注意是距离,不是相似度)。
表示顶点u和v之间距离为k(这里的距离k实际上是指距离小于等于k的节点集合)的环路上的结构距离(注意是距离,不是相似度)。
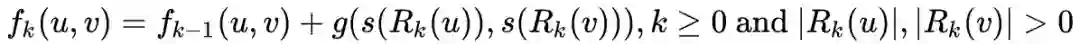
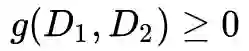 是衡量有序度序列
是衡量有序度序列
 和
和
 的距离的函数,并且
的距离的函数,并且
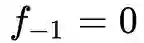 .
.
 和
和
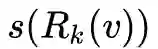 的长度不同,并且可能含有重复元素。所以文章采用了Dynamic Time Warping(DTW)来衡量两个有序度序列。
的长度不同,并且可能含有重复元素。所以文章采用了Dynamic Time Warping(DTW)来衡量两个有序度序列。
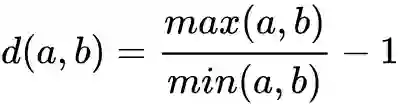
 情况下的距离为1,
情况下的距离为1,
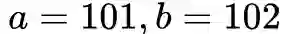 情况下的距离差异为0.0099。这个特性正是我们想要的。
情况下的距离差异为0.0099。这个特性正是我们想要的。
构建层次带权图
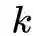 我们都可以计算出两个顶点之间的一个距离,现在要做的是通过上一节得到的顶点之间的有序度序列距离来构建一个层次化的带权图(用于后续的随机游走)。
我们都可以计算出两个顶点之间的一个距离,现在要做的是通过上一节得到的顶点之间的有序度序列距离来构建一个层次化的带权图(用于后续的随机游走)。
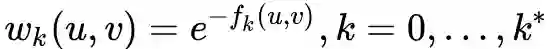
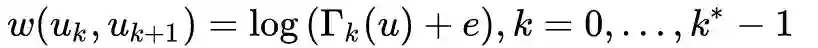
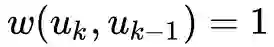
 是第k层与u相连的边的边权大于平均边权的边的数量。
是第k层与u相连的边的边权大于平均边权的边的数量。
 ,
,
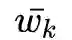 就是第k层所有边权的平均值。
就是第k层所有边权的平均值。
采样获取顶点序列
 中进行顶点序列采样。每次采样时,首先决定是在当前层游走,还是切换到上下层的层游走。
中进行顶点序列采样。每次采样时,首先决定是在当前层游走,还是切换到上下层的层游走。
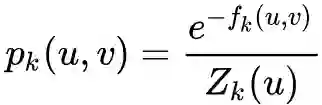 其中
其中
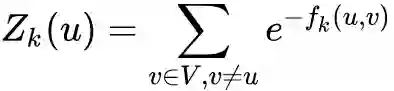 是第k层中关于顶点u的归一化因子。
是第k层中关于顶点u的归一化因子。
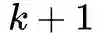 层或
层或
 层,
层,

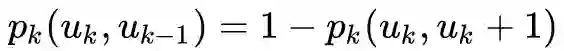
三个时空复杂度优化技巧:
OPT1 有序度序列长度优化
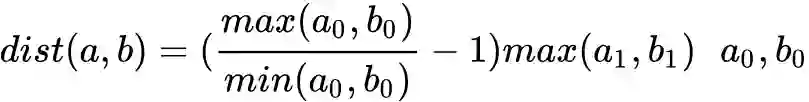 为度数,
为度数,
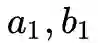 为度的出现次数。
为度的出现次数。
OPT2 相似度计算优化
 的时候他们的距离也已经非常大了,那么在随机游走时这样的边就几乎不可能被采样到,所以我们也没必要计算这两个顶点之间的距离。
的时候他们的距离也已经非常大了,那么在随机游走时这样的边就几乎不可能被采样到,所以我们也没必要计算这两个顶点之间的距离。
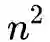 数量级缩减到
数量级缩减到
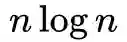 。
。
OPT3 限制层次带权图层数
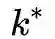 决定的。但是对很多图来说,图的直径会远远大于顶点之间的平均距离。
决定的。但是对很多图来说,图的直径会远远大于顶点之间的平均距离。
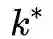 时,环上的度序列
时,环上的度序列
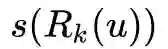 长度也会变得很短,
长度也会变得很短,
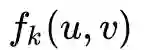 和
和
 会变得接近。
会变得接近。
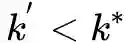 ,使用最重要的一些层来评估结构相似度。
,使用最重要的一些层来评估结构相似度。
Struc2Vec 核心代码
顶点对距离计算
_get_order_degreelist_node
,这个函数的作用是计算顶点
root
对应的有序度序列,也就是前面提到的
 。
。
root
开始进行遍历,遍历的过程计算当前访问的层次
level
,就是对应文章中的
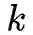 。每次进行节点访问时只做一件事情,就是记录该顶点的度数。当
。每次进行节点访问时只做一件事情,就是记录该顶点的度数。当
level
增加时,将当前
level
中的度序列(如果使用优化技巧就是压缩度序列)排序,得到有序度序列。函数的返回值是一个字典,该字典存储着
root
在每一层对应的有序度序列。
_compute_ordered_degreelist
函数就很简单了,用一个循环去计算每个顶点对应的有序度序列。
def _get_order_degreelist_node(self, root, max_num_layers=None):
if max_num_layers is None:
max_num_layers = float('inf')
ordered_degree_sequence_dict = {}
visited = [False] * len(self.graph.nodes())
queue = deque()
level = 0
queue.append(root)
visited[root] = True
while (len(queue) > 0 and level <= max_num_layers):
count = len(queue)
if self.opt1_reduce_len:
degree_list = {}
else:
degree_list = []
while (count > 0):
top = queue.popleft()
node = self.idx2node[top]
degree = len(self.graph[node])
if self.opt1_reduce_len:
degree_list[degree] = degree_list.get(degree, 0) + 1
else:
degree_list.append(degree)
for nei in self.graph[node]:
nei_idx = self.node2idx[nei]
if not visited[nei_idx]:
visited[nei_idx] = True
queue.append(nei_idx)
count -= 1
if self.opt1_reduce_len:
orderd_degree_list = [(degree, freq)
for degree, freq in degree_list.items()]
orderd_degree_list.sort(key=lambda x: x[0])
else:
orderd_degree_list = sorted(degree_list)
ordered_degree_sequence_dict[level] = orderd_degree_list
level += 1
return ordered_degree_sequence_dict
def _compute_ordered_degreelist(self, max_num_layers):
degreeList = {}
vertices = self.idx # self.g.nodes()
for v in vertices:
degreeList[v] = self._get_order_degreelist_node(v, max_num_layers)
return degreeList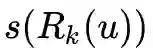 后,我们要做的就是计算顶点对之间的距离
后,我们要做的就是计算顶点对之间的距离
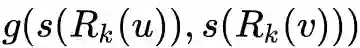 , 然后再利用公式
, 然后再利用公式

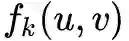
compute_dtw_dist
,该函数实现的功能是计算顶点对之间的距离
 ,参数
,参数
degreeList
就是前面一步我们得到的存储每个顶点在每一层的有序度序列的字典。
convert_dtw_struc_dist
的功能是根据
compute_dtw_dist
得到的顶点对距离完成关于
 的迭代计算。
的迭代计算。
self.opt2_reduce_sim_calc
函数会选择计算所有顶点对间的距离,还是只计算度数接近的顶点对之间的距离。
def compute_dtw_dist(part_list, degreeList, dist_func):
dtw_dist = {}
for v1, nbs in part_list:
lists_v1 = degreeList[v1] # lists_v1 :orderd degree list of v1
for v2 in nbs:
lists_v2 = degreeList[v2] # lists_v1 :orderd degree list of v2
max_layer = min(len(lists_v1), len(lists_v2)) # valid layer
dtw_dist[v1, v2] = {}
for layer in range(0, max_layer):
dist, path = fastdtw(
lists_v1[layer], lists_v2[layer], radius=1, dist=dist_func)
dtw_dist[v1, v2][layer] = dist
return dtw_dist
def _compute_structural_distance(self, max_num_layers, workers=1, verbose=0,):
if os.path.exists(self.temp_path+'structural_dist.pkl'):
structural_dist = pd.read_pickle(
self.temp_path+'structural_dist.pkl')
else:
if self.opt1_reduce_len:
dist_func = cost_max
else:
dist_func = cost
if os.path.exists(self.temp_path + 'degreelist.pkl'):
degreeList = pd.read_pickle(self.temp_path + 'degreelist.pkl')
else:
degreeList = self._compute_ordered_degreelist(max_num_layers)
pd.to_pickle(degreeList, self.temp_path + 'degreelist.pkl')
if self.opt2_reduce_sim_calc:
degrees = self._create_vectors()
degreeListsSelected = {}
vertices = {}
n_nodes = len(self.idx)
for v in self.idx: # c:list of vertex
nbs = get_vertices(
v, len(self.graph[self.idx2node[v]]), degrees, n_nodes)
vertices[v] = nbs # store nbs
degreeListsSelected[v] = degreeList[v] # store dist
for n in nbs:
# store dist of nbs
degreeListsSelected[n] = degreeList[n]
else:
vertices = {}
for v in degreeList:
vertices[v] = [vd for vd in degreeList.keys() if vd > v]
results = Parallel(n_jobs=workers, verbose=verbose,)(
delayed(compute_dtw_dist)(part_list, degreeList, dist_func) for part_list in partition_dict(vertices, workers))
dtw_dist = dict(ChainMap(*results))
structural_dist = convert_dtw_struc_dist(dtw_dist)
pd.to_pickle(structural_dist, self.temp_path +
'structural_dist.pkl')
return structural_dist构建带权层次图
_get_transition_probs
实现。
layers_adj
存储着每一层中每个顶点的邻接点,
layers_distances
存储着每一层每个顶点对的结构化距离。
_get_transition_probs
只做了一件事情,就是逐层的计算顶点之间的边权
 ,并生成后续采样需要的alias表。
,并生成后续采样需要的alias表。
def _get_transition_probs(self, layers_adj, layers_distances):
layers_alias = {}
layers_accept = {}
for layer in layers_adj:
neighbors = layers_adj[layer]
layer_distances = layers_distances[layer]
node_alias_dict = {}
node_accept_dict = {}
norm_weights = {}
for v, neighbors in neighbors.items():
e_list = []
sum_w = 0.0
for n in neighbors:
if (v, n) in layer_distances:
wd = layer_distances[v, n]
else:
wd = layer_distances[n, v]
w = np.exp(-float(wd))
e_list.append(w)
sum_w += w
e_list = [x / sum_w for x in e_list]
norm_weights[v] = e_list
accept, alias = create_alias_table(e_list)
node_alias_dict[v] = alias
node_accept_dict[v] = accept
pd.to_pickle(
norm_weights, self.temp_path + 'norm_weights_distance-layer-' + str(layer)+'.pkl')
layers_alias[layer] = node_alias_dict
layers_accept[layer] = node_accept_dict
return layers_accept, layers_alias前面的部分仅仅得到了在同一层内,顶点之间的转移概率,那么同一个顶点在不同层之间的转移概率如何得到呢?
下面的prepare_biased_walk就是计算当随机游走需要跨层时,决定向上还是向下所用到的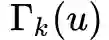
def prepare_biased_walk(self,):
sum_weights = {}
sum_edges = {}
average_weight = {}
gamma = {}
layer = 0
while (os.path.exists(self.temp_path+'norm_weights_distance-layer-' + str(layer))):
probs = pd.read_pickle(
self.temp_path+'norm_weights_distance-layer-' + str(layer))
for v, list_weights in probs.items():
sum_weights.setdefault(layer, 0)
sum_edges.setdefault(layer, 0)
sum_weights[layer] += sum(list_weights)
sum_edges[layer] += len(list_weights)
average_weight[layer] = sum_weights[layer] / sum_edges[layer]
gamma.setdefault(layer, {})
for v, list_weights in probs.items():
num_neighbours = 0
for w in list_weights:
if (w > average_weight[layer]):
num_neighbours += 1
gamma[layer][v] = num_neighbours
layer += 1
pd.to_pickle(average_weight, self.temp_path + 'average_weight')
pd.to_pickle(gamma, self.temp_path + 'gamma.pkl')随机游走采样
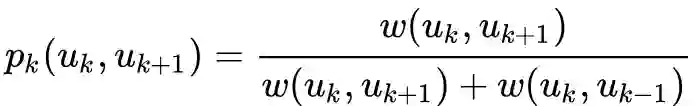
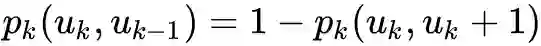
def _exec_random_walk(self, graphs, layers_accept,layers_alias, v, walk_length, gamma, stay_prob=0.3):
initialLayer = 0
layer = initialLayer
path = []
path.append(self.idx2node[v])
while len(path) < walk_length:
r = random.random()
if(r < stay_prob): # same layer
v = chooseNeighbor(v, graphs, layers_alias,
layers_accept, layer)
path.append(self.idx2node[v])
else: # different layer
r = random.random()
try:
x = math.log(gamma[layer][v] + math.e)
p_moveup = (x / (x + 1))
except:
print(layer, v)
raise ValueError()
if(r > p_moveup):
if(layer > initialLayer):
layer = layer - 1
else:
if((layer + 1) in graphs and v in graphs[layer + 1]):
layer = layer + 1
return pathStruc2Vec 应用
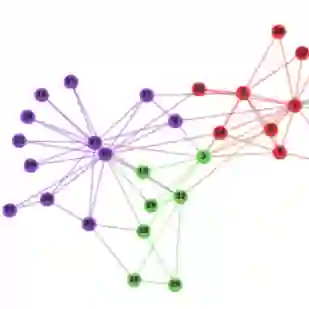
Struc2Vec应用于无权无向图(带权图的权重不会用到,有向图会当成无向图处理),主要关注的是图中顶点的空间结构相似性,这里我们采用论文中使用的一个数据集。该数据集是一个机场流量的数据集,顶点表示机场,边表示两个机场之间存在航班。机场会被打上活跃等级的标签。
这里我们用基于空间结构相似的Struc2Vec和基于近邻相似的Node2Vec做一个对比实验。
本例中的训练,评测和可视化的完整代码在下面的git仓库中,
https://github.com/shenweichen/GraphEmbedding
分类
Struc2Vec结果 micro-F1: 0.7143, macro-F1: 0.7357
Node2Vec结果 micro-F1: 0.3571, macro-F1: 0.3445
差距还是蛮大的,说明Struc2Vec确实能够更好的捕获空间结构性。
可视化
Struc2Vec结果
Node2Vec结果
今天的分享就到这里,谢谢大家。
如果您喜欢本文,欢迎点击右上角,把文章分享到朋友圈~~
社群推荐:
欢迎加入 DataFunTalk 推荐算法 交流群,跟同行零距离交流。如想进群,请加逃课儿同学的微信 ( 微信号:datafun-coco ),逃课儿会自动拉你进群。

 福利来了
福利来了 
用户画像技术及方法论
关于我们:
一个在看,一段时光!👇