修订 | 从无穷小量的角度看微积分定义（目录篇）

[遇见数学] 专栏作者介绍: 毛线团君

双鸭山数学学院某肥宅，梦想是无戒口地吃，无限时地睡，无止境地学。_(:3」∠)_

2018.12.30 修改"求个导试试"下中的式子中错误, 非常感谢 @H.K.Zhang 朋友指正!

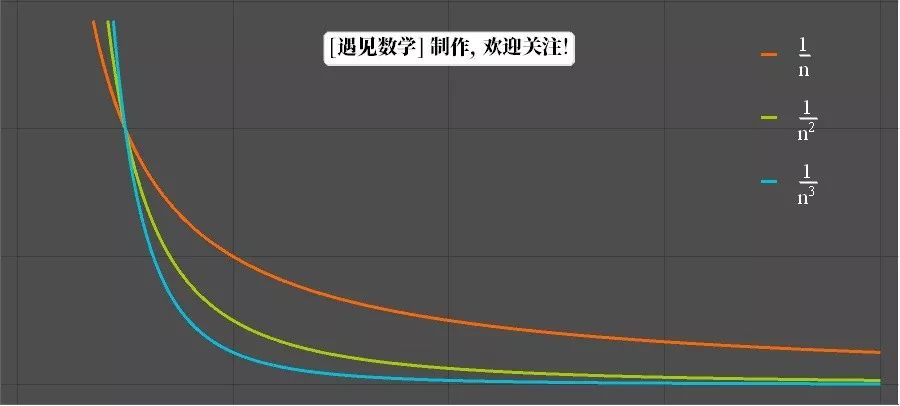
上一节中讲到了数学中的《无穷小量是分层》的。我们提及了一个无穷小量的比较方式：

所以  这个无穷小量比  要高阶。

那么我们把  换元成 ，得到 ，就是我们日常所说的 ，这是一个无限接近0的变量，而不是一个定值。

你可能没有意识到这个  有多么伟大。这牵扯到了第二次数学危机中的情景。牛顿和莱布尼茨同时发明了微积分以后，微积分成为了一项解决实际问题的伟大工具。直到一位叫做贝克莱的哲学家提出了一个问题："为什么求导的过程中的无穷小量，一开始当成不是 0 计算，后来又被当成了 0 算？它是'消失的量的幽灵'吗？"

为了理解他这个问题，我们来求个导试试。

稍微展开来说，
1.函数的连续性意味着告诉你，当  时无穷小量的时候，也是一个无穷小量，但是连续性的定义不关心它是一个什么样的无穷小量。如果  不是无穷小量，那么这个函数在这点就不连续。

2.在可导性的定义中，我们把  理解为一个与  同阶的无穷小量 ( f'(x) 为0的时候不一定是高阶无穷小量，一般是个常数 0)，如果  是一个比  低阶的无穷小量或者不是无穷小量，那函数在这点就不可导。

3.在可微性的定义中， 是一个比  高阶的无穷小量，如果不是高阶无穷小量，那么这个函数在这点就不可微。

4.在黎曼可积的定义中，讨论 。当区间  被分成  小段，其中最大的区间长度为无穷小时，所有区间里面函数的最大值  和最小值  的差的上界  是个无穷小量，并且  依旧是个无穷小量。这就是高数书上难以理解的达布上和与达布下和之差，从无穷小量的角度来理解的定义。
这是一个纲领，接下来会讲述更多的无穷小量的故事。