辛普森的悖论：如何用相同的数据证明相反的论点

来源：Medium

编译：Bot

对于数据科学家而言，了解统计现象和问“为什么”是非常重要的。

想象这样一个场景：一天，你和朋友约好了一起吃晚饭，你们俩都想找一家完美的餐厅。由于选项太多，两人今天的口味也不一定一样，为了避免长达数小时的争论，你们保守地采用了现代人常用的一种方法：查看美食评论。

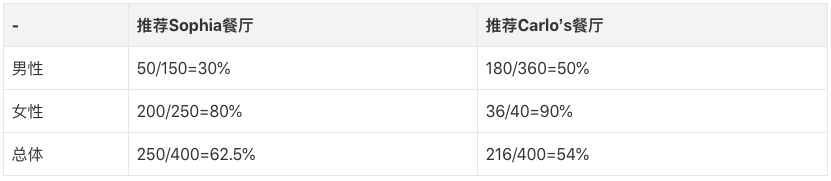
在用同一个APP看了所有餐厅后，最终你们锁定了其中的两家：Carlo's餐厅和Sophia餐厅。你更喜欢Carlo's，因为从两性数据上看来，无论是男性用餐者还是女性用餐者，他们给出的好评率都更高（例：男性好评率=男性好评数/男性评论总数）；而你的朋友更倾向于Sophia，因为他发现从整体上来看，Sophia的好评率更高，口味应该更大众。

那么这到底是怎么回事？是APP统计错误了吗？事实上，这两个统计结论都是正确的，只是你们在不知不觉中已经走进了辛普森悖论。在这里，我们能用完全相同的一组数据证明两个全然相反的论点。

什么是辛普森悖论？

辛普森悖论得名于英国统计学家E.H.辛普森（E.H.Simpson），这是他于1951年阐述的一种现象：当我们以分组和聚合两种方式统计同一数据集时，最后得出的两个趋势可能是完全逆转的。在上面这个“吃饭”案例中，Carlo's餐厅的两性推荐率更高，但它的总体推荐率却低了。如果不想被绕晕，我们可以用一些直观的数据来说明：

上表清楚地表明，当数据分组时，Carlo's是首选，但是当数据合并时，Sophia是首选！

导致这一悖论的原因是样本大小。当我们分组统计数据时，Carlo's餐厅的女性推荐率高达90%，但它的样本只有40个，只占总评论人数的10%；而Sophia餐厅的女性推荐率虽然只有80%，但女性评论者有250个，这显然会大幅拉高餐厅的总体好评率。

所以在挑选餐厅时，我们事先要确定数据的统计方法，是合并更合理，还是分组更合理——这取决于数据生成的过程，即数据的因果模型。

相关性的逆转

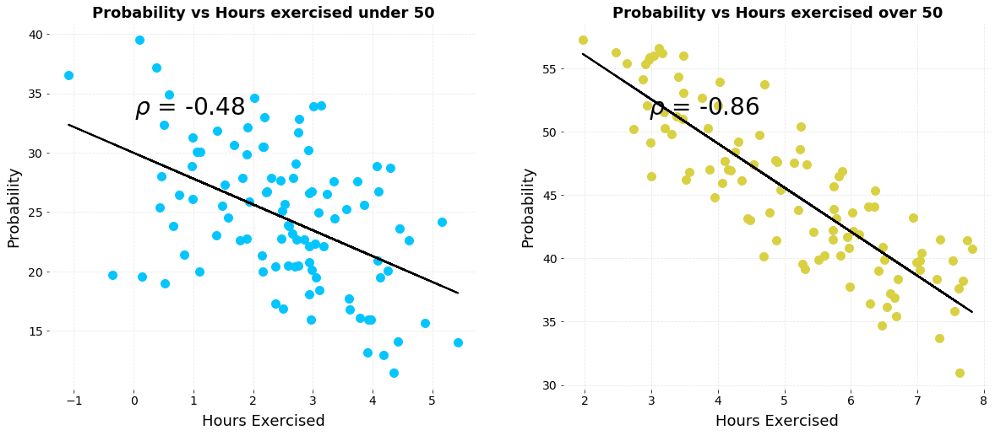
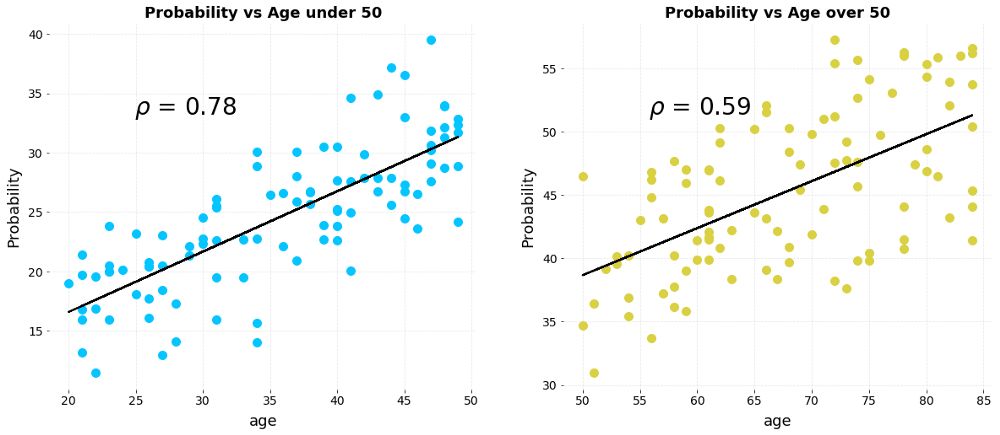
在我们的生活中，另一种常见的辛普森悖论是分组、聚合讨论数据后，元素之间的相关性也出现了逆转。举一个简单的例子，假设我们有50岁以上和50岁以下两组患者，在收集了他们的每周运动小时数和病发风险后，我们得到了下面两幅有关运动和病情恶化几率关系的图表：

左：50岁以下；右：50岁以上（横坐标为运动小时数，纵坐标为恶化风险）

上图很清楚地表明两者是负相关的，每周运动得越久，患者病情恶化的可能性就更低。但是，如果我们把两组数据结合在一起：

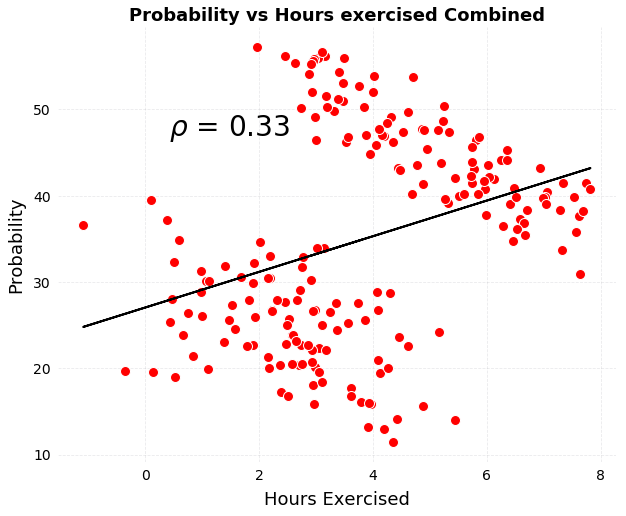
全年龄段患者的运动小时数和病情恶化几率关系图

运动和病情恶化的相关性就完全逆转了！如果只呈现这一幅图，最后我们得出的结论会是运动增加恶化几率。同一组数据，截然不同的结论，同样的，这个例子的问题也在于数据生成过程——我们没能收集完整的成因数据，自然也解释不了最终结果。

解决悖论

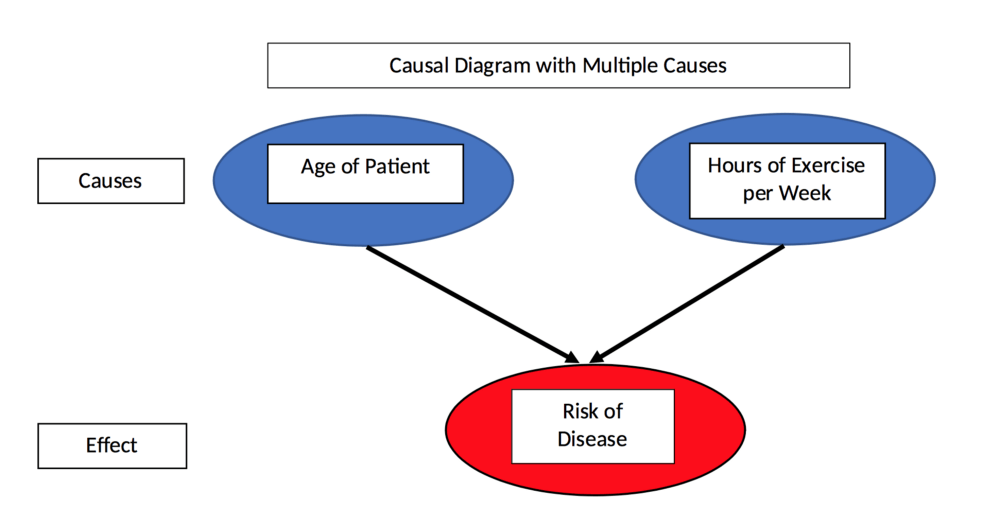
为了避免辛普森的悖论导致我们得出两个相反的结论，最直接的方法是决定分组还是聚合。这看起来很简单，但做起来并不容易。要做对选择题，首先我们要考虑因果关系：数据是怎么产生的？影响结果的因素有哪些？其中有哪些是我们没有呈现的？

以运动和病情恶化的分析为例，很明显，运动肯定不是影响病情加重的唯一因素，饮食、环境、遗传……它的影响因素非常复杂。但在上图中，我们只看到了恶化几率和运动时长之间的关系，在没有控制变量的情况下，这相当于假设恶化只是由运动引起的，显然不合理。

例如，如果我们考虑了原数据中被忽略的那个因素：年龄。

通过下图我们可以发现，无论是50岁以下还是50岁以上，患者的年龄和病情恶化几率都显示出强烈正相关。这意味着随着患者年龄增加，即便每周运动量相同，老年患者也比年轻患者更容易病情恶化。

患者年龄和病情恶化几率关系图

在这种情况下，分组讨论数据是规避辛普森悖论的一种方式。这和做科学实验一样，但凡数据间涉及因果关系，我们都应该在分析之前控制好变量，确保数据的合理分层。

而在选餐厅那个例子中，解决悖论的方法是重新审视自己想要解决的问题——既然目标是选择完美的餐厅，力求口味大众化，避免踩雷，那分性别统计就意义不大了。在那种情况下，聚合数据最有意义。

现实生活中的辛普森悖论

看到这里，也许有的读者会觉得这个悖论太简单了，它应该就只是统计学里的一个概念，不可能有人会犯这种错。但事实上，在现实世界中，我们确实也有许多著名的辛普森悖论研究案例。

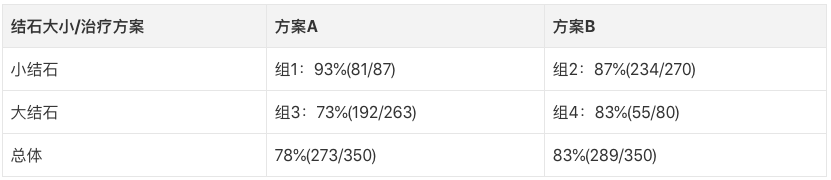
一个比较典型的例子是两种肾结石治疗方案的取舍。根据临床实验数据，医生发现在治疗小结石和大结石时，方案A都有更好的效果；但是如果综合两种肾结石来看，方案B的治愈率更高。下面是具体数据：

如果是你，你会选哪种治疗方案？这个问题要结合医疗领域的数据生成过程——因果模型。在实际操作中，就病情严重情况而言，大结石肯定比小结石严重得多，而方案A比方案B更具侵入性（医学上带有一定创伤性的治疗措施）。因此，如果患者的肾结石很小，医生一般会保守起见，采用方案B；而如果患者的肾结石很大，医生就会直接用效果最好的方案A。

由于方案A更适用于严重病例，它的总体治愈率肯定会低于方案B。

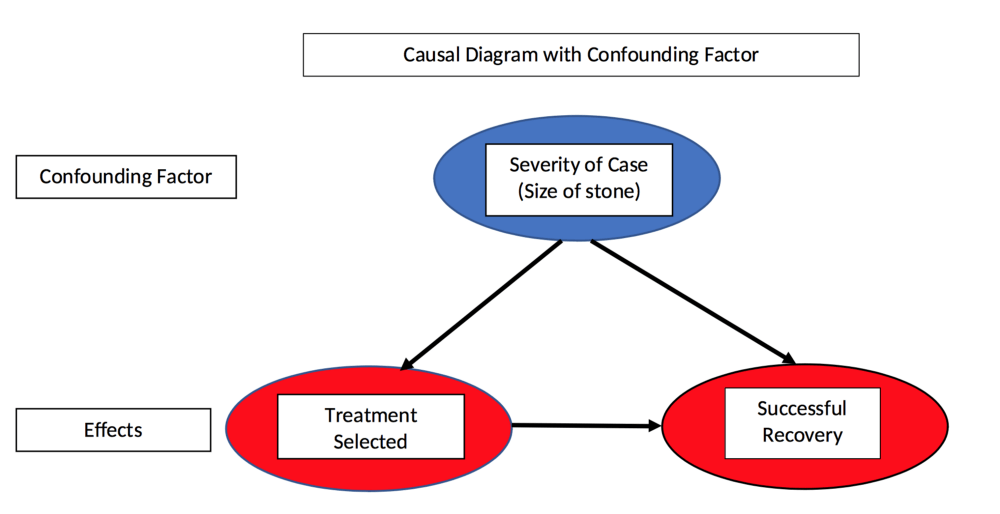
我们把这个例子中的“病情严重性”称为混淆变量，因为它和自变量（治疗方案）、因变量（治愈）均相关。我们是没法从数据中直接看到这个变量的，但如果绘制了因果关系图，一切就很明确了：

因果关系图和混淆变量

如上图所示，两种方案的治愈率都受所选择的治疗方案和结石大小影响，而选择治疗方案本身也受结石大小影响。这意味着如果要做全面定量实验，我们必须控制结石大小，比较两种方案的治愈率情况。根据实验结果，方案A的效果更好。

如果不做实验，我们换一种思路也能解答这个问题。如果患者的结石较小，治愈率更高的方案A更好；如果患者的结石较大，还是方案A更好。由于患者肯定会有或大或小的结石，综合来看，选择方案A肯定是效果最好的。

有时候，查看聚合数据很有用，但在一些情况下，它也可能模糊事件的真相。

另一个现实案例

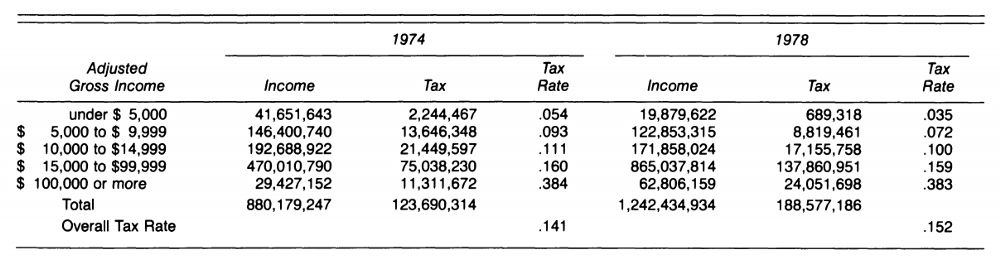
第二个现实案例是政治观点上的辛普森悖论。下表是杰拉尔德·福特担任美国总统期间的税收、税率变化，可以发现，从1974年到1978年，每个收入群体的税率都不同程度下降了，但社会整体税率却提高了。

所有个人税率均下降，但整体税率上升

根据前面的介绍，读到这里，相信大家应该已经学会了该如何解释这个悖论：寻找影响整体税率的其他因素。社会整体税率是两个因子的函数，它和各收入群体的税率有关，也和各收入群体的总收入金额相关。1978年，美国由于通货膨胀导致居民工资出现显著增长，国民整体收入提高，再加上高收入群体税率降低少，全国的整体税率实际上是提高了。

除了数据生成过程之外，是否汇总数据还应取决于我们想要回答的问题。仍以税收的例子为例，在个人层面上，我们只是个人，所以只关心自己的税率。但为了确定自己是不是多交税了，除了观察税率变化，我们还应该留意工资的增长情况。影响税率的重要因素有两个，而表格只提供了其中一个，由此得出的统计结果是不准确的。

辛普森悖论的重要性

辛普森悖论非常重要，因为它时刻在提醒我们，表格中显示的数据可能并不是所有数据。我们不能只满足于数字、数据，而必须关注数据的生成过程 ——因果模型——对数据负责。在大学里，对因果关系的思考并不是大多数数据科学家会在课上学到的技能，但是这能有效防止我们从数字中得出错误结论。一个真正好的数据科学家不仅是数据分析上的专家，他也能结合专业领域的知识，做出更好的决策。

数据是一种强大的武器，它可以是帮助我们了解世界的工具，也可以成为他人愚弄我们的帮凶。我们必须始终保持对数据的怀疑态度，理性思考，并多问“为什么”。

原文地址：towardsdatascience.com/simpsons-paradox-how-to-prove-two-opposite-arguments-using-one-dataset-1c9c917f5ff9