TensorFlow Lattice：灵活、可控、可解释的 ML

文 / Mahdi Milani Fard，软件工程师，Google Research 

大多数 ML 从业人员都遇到过这样一个典型情况：训练数据看起来与评估模型所用的运行时查询 (Run-time Queries) 完全不同。

如 DNN 或 Forest 这些仅依靠训练数据集的灵活 ML 解决方案，在遇到输入空间未包含的训练和验证数据集上，经常表现欠佳甚至失效。在可能违反重要策略或公平限制的情况下，可能会尤为不理想。

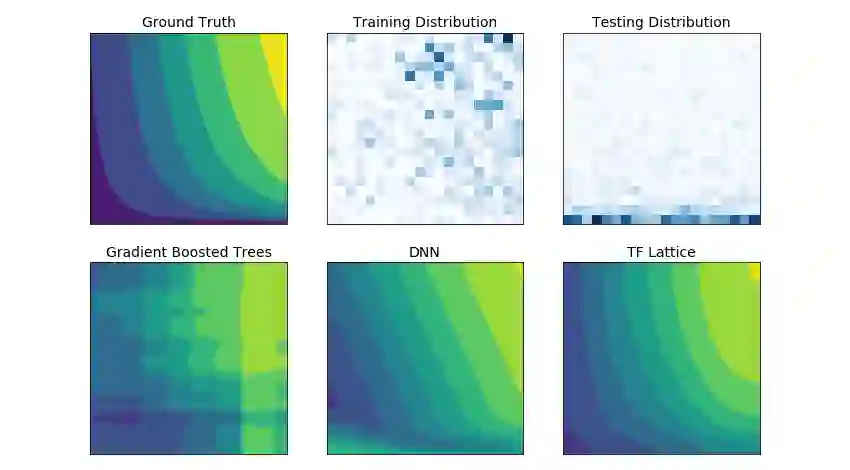
在覆盖训练数据很少的情况下，不受约束的模型可能会表现异常。图中，DNN 和 GBT（Gradient Boosted Trees，梯度提升树）的预测与测试数据的事实相去甚远

虽然使用常见形式的正则化就可以得到更合理的推理效果，但是标准正则化器无法保证整个输入空间（尤其输入的维度较高的时候）模型的合理表现。在切换到具有更多可控和可预测行为的更简单模型时，模型准确性则有可能大打折扣。

借助 TF Lattice，我们可以在使用灵活的模型的同时，借助其提供的几种可选的方案，通过使用有意义的常识信息或策略驱动的 形状约束 (Shape Constraints)，将领域知识注入学习过程之中。例如，您可以规定，模型输出相对于给定输入应呈单调递增。这些额外的领域知识不仅可以帮助模型学习训练数据集，还可以按照用户控制和期望的方式运行。

TensorFlow Lattice 库

TensorFlow Lattice 库可以用于训练受约束、可解释基于 点阵 (Lattice) 的模型。点阵是一张插值查询表，可以粗略计算数据中的任意输入输出关系。

上图是一个包含 2 个输入特征和 4 个参数（输入空间四个角上的函数值）的点阵函数简单示例；函数的剩余部分将通过这些参数插值得到。您可以使用更高维度的点阵和更高细粒度的参数网格来获得更灵活的函数。使用 tfl.layers.Lattice Keras 层来实现点阵。

TensorFlow Lattice 还提供分段线性函数（使用 tfl.layers.PWLCalibration 层），以将输入特征校准和归一化到点阵可接受的范围：在上面的示例点阵中为 0 到 1。

对于分类特征，TensorFlow Lattice 会为分类校准（使用 tfl.layers.CategoricalCalibration 层）提供同输入点阵的相似的输出。结合校准器和上面的点阵，我们可以得到一个已校准点阵模型。

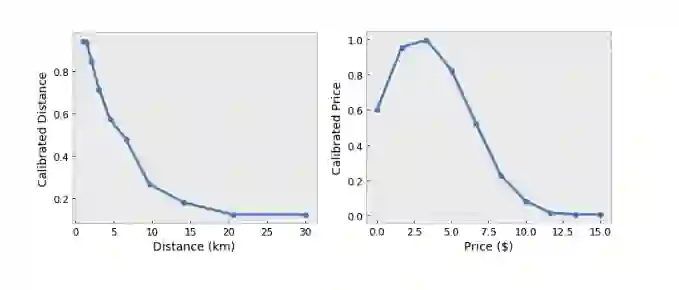
您可以在 TensorFlow Lattice 层上施加多种形式的约束，以将问题领域的知识注入训练过程中：

• 单调性：您可以规定，输出仅与与输入的增长/减少相对应。在我们的示例中，您可设想规定为：随着与咖啡店之间的距离增加，用户偏好程度降低。

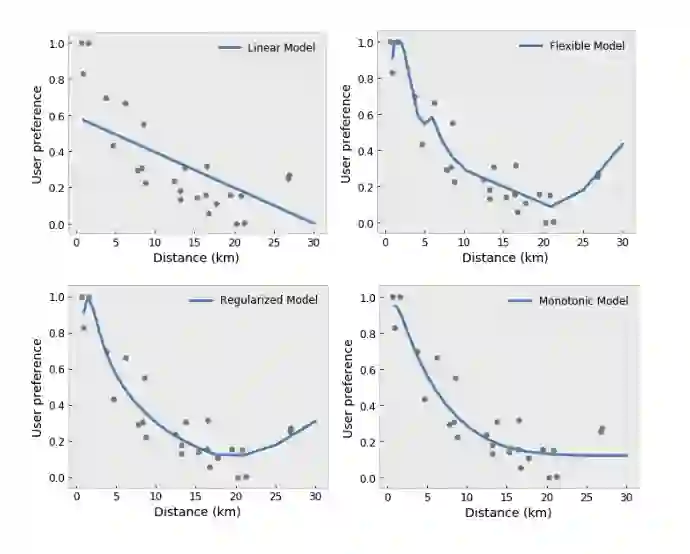
• 凸度/凹度：您可以规定函数形状的凸凹度。与单调性混合使用，上图中表示函数相对于给定特征来说收益递减。
• 单峰性：您可以规定，函数应有唯一的峰值或谷值。这使您可以表示相对于某一特征有最佳表现的函数。
• 成对信 任：此约束表明，一个输入特征在语义上反映出对另一特征的信任。例如，评论数量越多，您对餐馆的平均星级评分就会越有信心。当评论数量越多时，该模型将相对于星级评分更敏感（即相对于评分具有更大的斜率）。

• 成对优势：此约束表明，该模型应将一个特征看得比另一个特征更重要。可以通过确保函数的斜率相对于主要特征更大来实现。

除形状约束外，TensorFlow Lattice 还提供许多 正则化器 (Regularizer)，以按函数的每个特征分别控制灵活度和平滑度。其中包括 Laplacian 正则化器（用于更平坦的函数）、Hessian 正则化器（用于更线性的校准函数）、Wrinkle 正则化器（用于更平滑的校准函数）和 Torsion 正则化器（用于更共线性的点阵函数）。

示例：餐馆排名

此示例来自我们的端到端形状约束教程，其中涉及上述许多使用已封装估算器的约束。

设想这样一个场景：我们要确定用户是否会点击餐馆搜索结果。我们的任务是在给定输入特征的情况下预测点击率 (CTR)：

• 平均评分：范围在 1 到 5 之间的数字特征
• 评论数量：范围在 0 到 200 之间的数字特征

• 价格评分：分类特征，其值从“$”到“$$$$”表示为 0 到 3，缺失值表示为 -1

我们将这些作为领域知识来限制和控制模型的行为：

• 平均评分的输出呈单调递增
• 评论数量的输出呈单调递增，但伴随着收益递减
• 当有更多评论时，模型应更信任平均评分

• 与“$”餐厅相比，用户通常更喜欢“$$”餐厅

我们可以使用 TF Lattice 库提供的 Keras 层来构建已校准的点阵模型：

model = tf.keras.models.Sequential()
model.add(
   tfl.layers.ParallelCombination([
       # Feature: average rating
       tfl.layers.PWLCalibration(
           # Input keypoints for the piecewise linear function
           input_keypoints=np.linspace(1., 5., num=20),
           # Output is monotonically increasing in this feature
           monotonicity='increasing',
           # This layer is feeding into a lattice with 2 vertices
           output_min=0.0,
           output_max=1.0),
       # Feature: number of reviews
       tfl.layers.PWLCalibration(
           input_keypoints=np.linspace(0., 200., num=20),
           # Output is monotonically increasing in this feature
           monotonicity='increasing',
           # There is diminishing returns on the number of reviews
           convexity='concave',
           # Regularizers defined as a tuple ('name', l1, l2)
           kernel_regularizer=('wrinkle', 0.0, 1.0),
           # This layer is feeding into a lattice with 3 vertices
           output_min=0.0,
           output_max=2.0),
       # Feature: dollar rating
       tfl.layers.CategoricalCalibration(
           # 4 rating categories + 1 missing category
           num_buckets=5,
           default_input_value=-1,
           # Partial monotonicity: calib(0) <= calib(1)
           monotonicities=[(0, 1)],
           # This layer is feeding into a lattice with 2 vertices
           output_min=0.0,
           output_max=1.0),
   ]))
model.add(
   tfl.layers.Lattice(
       # A 2x3x2 grid lattice
       lattice_size=[2, 3, 2],
       # Output is monotonic in all inputs
       monotonicities=['increasing', 'increasing', 'increasing']
       # Trust: more responsive to input 0 if input 1 increases
       edgeworth_trusts=(0, 1, 'positive')))
model.compile(...)

生成的训练模型满足所有指定的约束，并且添加的正则化使函数更平滑：

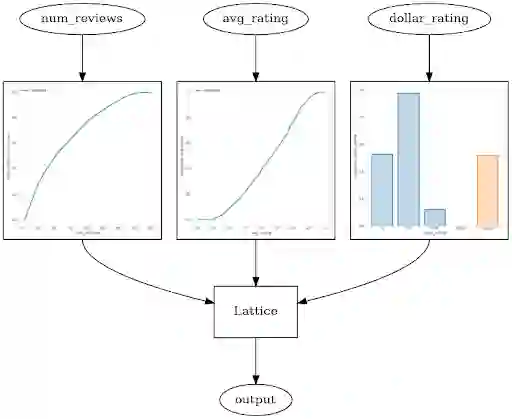
上述模型也可以使用 TF Lattice 库提供的已封装估算器构建。我们的形状约束教程中提供了一个 Colab 上的完整代码示例，对每个提到的约束的效果进行更细致的演示与说明。同时 TF Lattice Keras 层也可以与与其他 Keras 层搭配使用，以构建部分约束或正则化的模型。例如，可以在包含嵌入或其他 Keras 层的更深层网络的最后一层，使用点阵或 PWL（分段线性）校准层。感兴趣的朋友可以查看 Tensorflow Lattice 官方网站，来获取详尽的指南和教程，来帮助您入门：形状约束、已封装估算器、自定义估算器和 Keras 层。除此之外，您还可以查看在 TF 开发者峰会上我们的演示：

反馈

我们期待听到您对 TF Lattice 库的想法和意见。如要提交错误和 issue，请在 Github 上联系我们。

致谢

感谢以下人士为 TF Lattice 库的发布作出的杰出贡献：Oleksandr Mangylov、Mahdi Milani Fard、Taman Narayan、Yichen Zhou、Nobu Morioka、William Bakst、Harikrishna Narasimhan、Andrew Cotter 和 Maya Gupta。

相关论文

有关库中使用的模型和算法的更多详细信息，请查看我们关于点阵模型的刊发文章：

• 《单调性形态约束下的道义伦理学》(Deontological Ethics By Monotonicity Shape Constraints)，作者：Serena Wang、Maya Gupta，2020 年发表于国际人工智能与统计学会议 (AISTATS)
  https://arxiv.org/abs/2001.11990

• 《集合函数的形状约束》(Shape Constraints for Set Functions)，作者：Andrew Cotter、Maya Gupta、H. Jiang、Erez Louidor、Jim Muller、Taman Narayan、Serena Wang、Tao Zhu。2019 年发表于机器学习国际会议 (ICML)
  http://proceedings.mlr.press/v97/cotter19a.html

• 《用于可解释性和正则化的收益递减形状约束》(Diminishing Returns Shape Constraints for Interpretability and Regularization)，作者：Maya Gupta、Dara Bahri、Andrew Cotter、Kevin Canini，2018 年版《神经信息处理系统进展》(Advances in Neural Information Processing Systems (NeurIPS))
  https://papers.nips.cc/paper/7916-diminishing-returns-shape-constraints-for-interpretability-and-regularization

• 《深度点阵网络和部分单调函数》(Deep Lattice Networks and Partial Monotonic Functions)，作者：Seungil You、Kevin Canini、David Ding、Jan Pfeifer、Maya R. Gupta，2017 年版《神经信息处理系统进展》(Advances in Neural Information Processing Systems (NeurIPS))
  https://research.google.com/pubs/pub46327.html

• 《具有点阵集成的快速灵活单调函数》(Fast and Flexible Monotonic Functions with Ensembles of Lattices)，作者：Mahdi Milani Fard、Kevin Canini、Andrew Cotter、Jan Pfeifer、Maya Gupta，2016 年版《神经信息处理系统进展》(Advances in Neural Information Processing Systems (NeurIPS))
  https://papers.nips.cc/paper/6377-fast-and-flexible-monotonic-functions-with-ensembles-of-lattices

• 《单调校准插值查询表》(Monotonic Calibrated Interpolated Look-Up Tables)，作者：Maya Gupta、Andrew Cotter、Jan Pfeifer、Konstantin Voevodski、Kevin Canini、Alexander Mangylov、Wojciech Moczydlowski、Alexander van Esbroeck，2016 年发表于机器学习研究期刊 (JMLR)
  http://jmlr.org/papers/v17/15-243.html

• 《用于高效函数评估的优化回归》(Optimized Regression for Efficient Function Evaluation)，作者：Eric Garcia、Raman Arora、Maya R. Gupta，2012 年发表于《IEEE 图像处理事务》(IEEE Transactions on Image Processing)
  http://ieeexplore.ieee.org/document/6203580/

• 《点阵回归》(Lattice Regression)，作者：Eric Garcia、Maya Gupta，2009 年版《神经信息处理系统进展》(Advances in Neural Information Processing Systems (NeurIPS))
  https://papers.nips.cc/paper/3694-lattice-regression

如果您想详细了解 本文提及 的相关内容，请参阅以下文档。这些文档深入探讨了这篇文章中提及的许多主题：

• tfl.layers.Lattice
  https://tensorflow.google.cn/lattice/api_docs/python/tfl/layers/Lattice

• tfl.layers.PWLCalibration
  https://tensorflow.google.cn/lattice/api_docs/python/tfl/layers/PWLCalibration

• tfl.layers.CategoricalCalibration
  https://tensorflow.google.cn/lattice/api_docs/python/tfl/layers/CategoricalCalibration

• 形状约束教程
  

  https://tensorflow.google.cn/lattice/tutorials/shape_constraints

• Tensorflow Lattice 官方网站
  https://tensorflow.google.cn/lattice

• 形状约束
  https://tensorflow.google.cn/lattice/tutorials/shape_constraints

• 已封装估算器
  https://tensorflow.google.cn/lattice/tutorials/canned_estimators

• 自定义估算器
  https://tensorflow.google.cn/lattice/tutorials/custom_estimators

• Keras 层
  https://tensorflow.google.cn/lattice/tutorials/keras_layers

• Github
  https://github.com/tensorflow/lattice

—推荐阅读—