机器学习面试之各种混乱的熵

请听题：什么是熵？什么是交叉熵？什么是联合熵？什么是条件熵？什么是相对熵？它们的联系与区别是什么？

如果你感到回答这些问题有些吃力，对这些概念似乎清楚，似乎又没有那么明白，那这篇文章就是为你准备的。

1 从随机变量说起

假设有一枚硬币，将其抛出，落下后朝上的面为y。

这里的y是对未知量的一个表示。但它的值却是不确定的，可能取正面和反面两个值。

类似的不确定变量还有好多，比如说，将人的身高设为z,z中也包含了不确定性，因为不同的人身高是不一样的。

这类包含不确定性的变量我们称为随机变量。统计学就是研究这类不确定性变量的工具。

刻画随机变量最有力的一个工具就是它的概率分布。关于什么是概率分布，这里就不多说了，可以百度百科。

有了概率分布，我们可以说对一个随机变量有了完全的掌握，因为我们可以知道它可能取哪些值，某个值的概率是多少。

以上，是对基础知识的简单复习，下面开始进入正题。

2 什么是熵？

上面，我们知道，概率分布是对随机变量的刻画，不同的随机变量有着相同或不同的概率分布，熵，就是对不同概率分布的刻画！

为什么我们还需要对不同的概率分布进行刻画？

本质上，是为了描述不确定的程度，并以此对不同的概率分布进行比较。

请允许我举个栗子。

假如我告诉你，我有两枚硬币，一个上抛一次正面朝上概率是0.5,另一个是0.8。此时，假设两枚硬币上抛一次落下后朝上的面分别是x,y。

此时，我们可以很容易确定随机变量x,y的概率分布，并借此对两个随机变量有准确的掌握。

但我们要问，这两个随机变量哪个更随机？或者说，哪个随机变量包含的不确定性更大？

如果发挥直觉，我们可以感觉到，正面朝上概率为0.8的概率分布不确定性小于正面朝上概率为0.5的不确定性。

进一步思考，我们为什么会有这样的直觉？

因为我们是从“使用”概率分布的角度来思考问题的。也就是说，如果我们知道一枚硬币抛出后正面朝上概率为0.8，要比知道概率为0.5，更容易猜对硬币抛出后哪面朝上。

换句话说，0.8的概率分布比0.5的概率分布对我们来说，具有更大的信息量。

现在，我们对概率分布中的不确定性有了感性的认识，现在需要的是一个定量的指标，来衡量这个不确定性。想必你已经猜到了，这个指标就是熵。

3 熵的数学表达

熵应该是什么样子，才能表达出概率分布中的不确定性呢？

为了解决这个问题，我们来考察一下概率分布中的某个取值，以抛硬币为例，我们看正面这个取值。可以看到，取正面的概率越大，则不确定性就越小。概率越大，不确定性越小！请把这句话在心中默念三遍。

能够表达出概率越大，不确定性越小的表达式就是：

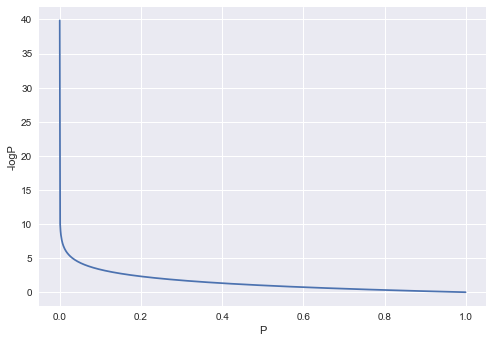
-logP

为了让大家有一个感性的认识，我特意画了一个图：

上图中的纵轴为-logP，横轴为P。

然后，我们继续思考，上面的-logP只是衡量了某个概率的不确定性，一个概率分布包含多个概率，而且概率相加等于1，一个概率大，必然会有其他的概率小。还是以抛硬币为例，0.8概率的正面，不确定性固然很小，但同时会造成反面的概率为0.2，不确定性比较大。这意味着，我们猜对一次抛硬币正面朝上的难度比较小，但要猜对一次反面朝上的难度就比较大。很显然，我们要衡量一个概率的分布的不确定性，就要综合衡量所有概率表达的不确定性。也就是求一个概率分布综合的不确定性。当当当当当！熵正式出场！

-∑PlogP

这个指标可以理解成概率分布的不确定性的期望值。这个值越大，表示该概率分布不确定性越大。它为我们人类提供的“信息”就越小，我们越难利用这个概率分布做出一个正确的判断。从这个角度，我们可以看到，熵是对概率分布信息含量的衡量，这与它是不确定性的衡量，其实是两种解读方式而已。

4 伯努利分布的熵

对于抛硬币判正反面来说，它的概率分布是伯努利分布，我们假设正面朝上的概率为p，则反面朝上的概率为（1-p)，它的熵就是：

H(p) = -plogp -(1-p)log(1-p)

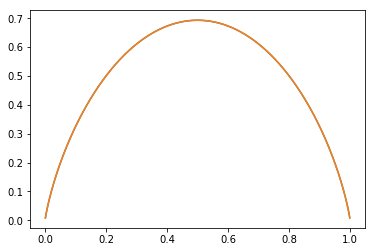
我们把它画出来就是这样。

可以看到，p=0.5时，伯努利分布的熵达到最大。这与我们的经验常识一致，因为此时，硬币朝上还是朝下完全是随机的，不确定性最大。

当p趋向于0时，熵也趋向于0，举个极端例子，如果硬币以概率1正面朝上，概率0反面朝上，则完全没有不确定性，所以熵就是0，因为熵是对不确定性的一个测量。

再来思考一个问题，我们说熵是描述不确定性的，在概率论中，不是有一个方差可以用来描述变量变化程度的吗，它和熵是什么关系呢？

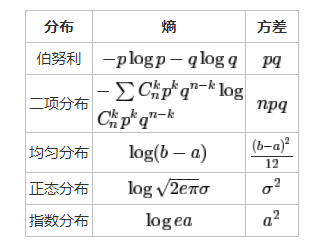
直觉上，方差越大，不确定性就越大，熵就应该越大，事实上确实如此，请看下图：

variance_entropy

对我们投硬币的伯努利分布，方差pq的最大值在p=0.5时取得，由上文我们知道，这也是熵取得最大值的p值。

对于正态分布，我们可以看到，期望对熵没有影响，只有方差才对熵有影响。这于我们的直觉也是相符的。

以上，我们尽可能从直觉的角度分析出了熵的表达式，也查看了几种分布的熵，以及它们和该分布的方差的关系，发现二者要描述的含义具有内在一致性。至此，我们终于可以说一窥熵的庐山真面目了。

下面，我们开始讨论由熵引出的各种其他熵，也就是本文文首提出的那些。

5 联合熵

虽然文首提出了那么多熵，但它们之间是有内在联系的，所以，我们尽可能按照它们的内在关系开展学习，先从联合熵说起。

联合熵与联合概率分布有关，对于随机变量X和Y，二者的联合概率分布为p(x,y),则这个联合概率分布的熵就叫做联合熵：

H(x,y) = -Σp(x,y)log(p(x,y))

我们假设X和Y都服从伯努利分布，且相互独立，可以把二者想象为上面的抛硬币，这样思考可以有所依托，不至于太抽象。X正面朝上的概率为p1，Y正面朝上的概率为p2，那么，它们的联合熵是多少呢？

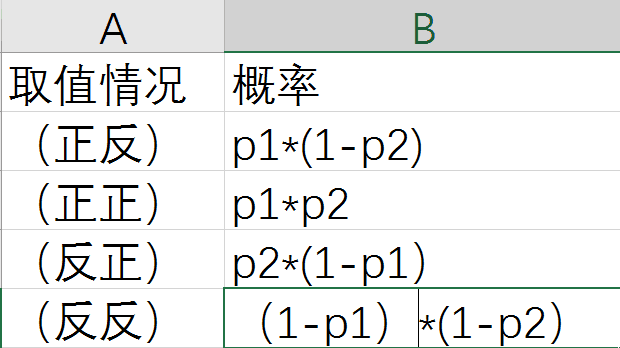
显然，我们需要找出联合概率分布，如下图所示：

association

上面就是联合分布，自然可以据此算出它的熵，由于表达式写出来太麻烦，这里就省去了，感兴趣的可以自己写一下。

我们关心的问题是，H(x,y)和H(x),H(y)有什么关系呢？

这里不想进行繁杂的数学证明，而是要继续用我们的直觉来帮助思考。查看上图，我们和Y的概率分布进行对比。

Y原先只有两个概率p2和(1-p2)，联合分布却有四个概率，这四个概率又可以认为是将Y的每个概率进行了分拆，p2 被分成了p2\*p1和p2\*(1-p1)。也就是说，对于Y的每个取值，本身就具有一个不确定性(p2)，由于要与X联合起来，就在每个取值的不确定性上又引入了不确定性，不确定性显然是增大了。

如果你理解了上面关于熵的含义，那么，不难想出，H(x,y)肯定是大于等于H(x)和H(y)的。仅当X没有不确定性时，比如永远是正面朝上，此时，在Y的基础上联合X，并没有引入新的不确定性，所以，H(x,y)=H(y)。

以上，我们没有运用数学，仅仅依靠感性直觉的思考就确定了联合熵的一些性质，可见，善于运用直觉是很重要的。

6 条件熵

现在我们知道，x,y的联合熵大于等于x和y单独的熵，对于y来说，引入的x增大了熵，那么，x的引入增加了多大的熵呢？这就是条件熵。

H(x|y) = H(x,y) - H(y)

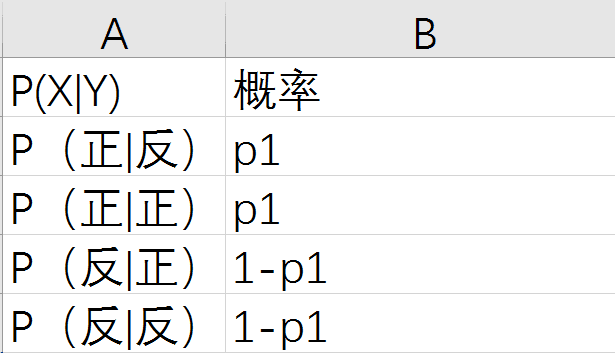
这里，有一个容易搞错的地方，H(x|y)叫做条件熵，它可不是条件概率p(x|y)的熵。为啥？因为p(x|y)压根就不是一个概率分布！！！还是以上面的两枚硬币为例，我们来计算一下p(x|y),注意，我们的例子中**假设x，y是相互独立的**。

condition

可见，所有的P(x|y)相加是2，根本就不是一个概率分布。有人可能会说，那为什么要叫条件熵，这不是故意误导人吗！

这是因为，条件熵的计算，和条件概率还是有点关系的。如下：

H(x|y) = - Σp(x,y)log(p(x|y))

这个公式可以由上面的熵的定义和条件熵的定义推导得出，这里就不推导了，感兴趣的可以自己推导下，并不难。

这里我们再分析一下条件熵H(x|y)与H(x)的关系，仍然用直觉法。条件熵是在Y上引入X后增加的不确定性，从感觉上，增加的不确定性无论如何不可能大于X本身自有的不确定性，也就是：

H(x|y) <= H(x)

仅当x，y相互独立时，等号才成立。

这个结论是我们感性认识到的，事实上，也可以进行证明得到。

学习过《统计学习方法》的同学，肯定对里面的信息增益概念有所了解，其实，我们仍然可以用直觉来理解这个概念。

不过，我们需要换种方式解读H(x|y) <= H(x)

之前，我们得出这个结论，是说Y上引入的X增加的不确定性不能大于X本身的不确定性。换个角度，X原有的不确定性是H(x)，现在我们引入Y，得到了联合的不确定性H(x,y)，从这个不确定性中减去Y自身带来的不确定性H(Y)，剩下的就是H(x|y),这个值小于等于H(x)，说明什么？说明，由于Y的引入，X的不确定性变小了，不确定性变小，就是信息含量的增加。不确定性变小的多少就是信息增益：

gain(X) = H(x) - H(x|y)

信息增益也叫做互信息。二者完全一样。

Note:

这里简单说下我对李航书的看法，一句话：不适合用来入门！只适合用来提高和面试准备。我意见比较大的是对逻辑回归的推导，不优雅。回头，我会专门写一篇逻辑回归的推导文章。

7 相对熵（又叫互熵，KL散度）

把相对熵放到最后来讲，是因为它和前面的几个概念联系不大。

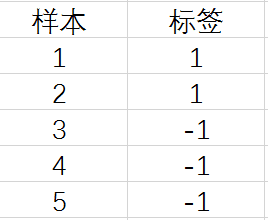
假设我们有如下5个样本：

huxinxi

我们要以此推导出标签的真实分布。假设标签的真实分布是q(x)，x取值为1和-1

为了确定q(x)在x=1和x=-1处的值，我们当然要运用最大似然法则。最大似然函数是：

q(x=1)\*q(x=1)\*q(x=-1)\*q(x=-1)\*q(x=-1)

如果你最大似然函数理解上有困难，建议补充一下这方面的知识，因为这个知识点在机器学习中运用的太多，确实无法绕过，逻辑回归本质上也是用的最大似然函数。

对上面的式子做合并处理，得到：

q(x=1)^2\*q(x=-1)^3

进一步，对上面的式子开5次方，得到：

q(x=1)^(2/5)\*q(x=-1)^(3/5)

假设p(x)就是由样本中统计出来的标签分布

2/5就是p(x=1)

3/5就是p(x=-1)

所以，对上面的式子进行规整就得到最大似然函数最终表达式：

Πq(x)^(p(x))

再取对数就是

Σp(x)log(q(x))

再取负号就是

d= -Σp(x)log(q(x))

最大化似然函数就是最小化d。

心急的朋友可能在想，说了半天，互熵到底是啥？现在就给出定义：

D(q||p) = d - H(p)

这里的d就是我们上面得到的d。

互熵描述的是什么呢？如何从直觉上进行理解？毕竟，上面用最大似然推出互熵还是有点太数学了。

这里，我们需要观察一下d，假设q和p完全相同，那么d就是H(p),互熵D也就等于0了。

同理，q和p越接近，越相同，则D就越小。互熵D(q||p)实际上就是在衡量我们通过计算得出的真实分布的表达式q，究竟与由样本统计得来的分布p有多接近，在衡量多接近这个概念时，我们运用到了熵的形式。

8 交叉熵

交叉熵放到最后，因为它最简单，它就是上面得出的d！

我们可以体会一下为什么叫做交叉熵，交叉是什么含义？

d= -Σp(x)log(q(x))

原本，p的熵是-Σp(x)log(p(x))，q的熵是-Σq(x)log(q(x))

现在，把p熵的log成分换成q(x), q熵的log成分换成p(x),（这里做了一个“交叉”！）就是

d= -Σp(x)log(q(x))      d2 = -Σq(x)log(p(x))

 d 就是p和q的交叉熵，

d2就是q和p的交叉熵。

从中我们也体会到，交叉熵是不满足交换律的，也就是说p和q的交叉熵与q和p的交叉熵是不一样的。

9 无总结，不进步

以上，是我对各种熵的概念的一些理解和感悟，分享出来，希望能够帮助到需要的朋友，当然，由于是个人理解，难免有不到位，甚至错误的地方，还望各路大神多多批评指正！

出处：https://www.jianshu.com/p/09b70253c840

版权申明：内容来源网络，版权归原创者所有。除非无法确认，我们都会标明作者及出处，如有侵权烦请告知，我们会立即删除并表示歉意。谢谢。

架构文摘

ID：ArchDigest

互联网应用架构丨架构技术丨大型网站丨大数据丨机器学习

更多精彩文章，请点击下方：阅读原文