深度学习中的不可导操作(次梯度和重参数化)

深度学习中的绝大多数模型都是靠求导梯度下降来进行参数更新. 但是如果遇到不可求导的操作该怎么办? 这时候如何优化我们的模型呢.

本文盘点了深度学习中的不可导操作(次梯度和重参数化).

主要包括两大类

[TOC]

image-20200116220613949

次梯度

深度学习算法通常需要反向传播来进行优化,这就涉及到求导的问题. 激活函数需要满足单调,处处可导,有界等条件. 如传统的sigmoid函数,但是现在很多激活函数并不是处处可导的.

如ReLU函数

其图像如下

img

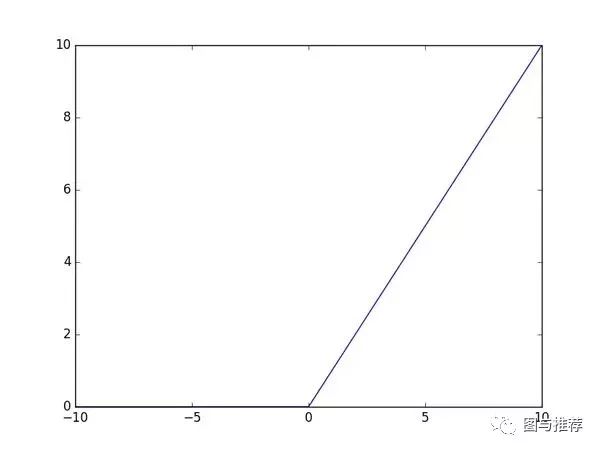
很明显在 处不可导,那么如何实现反向传播和模型优化呢? 答案就是:次梯度

次梯度

对于ReLU函数, 当x>0的时候,其导数为1; 当x<0时,其导数为0. 则ReLU函数在x=0的次梯度是  ,这里是次梯度有多个,可以取0,1之间的任意值. 工程上为了方便取c=0即可.

作者在面试阿里Research Intern的时候被面试官问到了这个问题...

重参数技巧

VAE中对高斯分布的重参数

这里是对连续分布的重参数.

VAE中隐变量z一般取高斯分布,即 ,然后从这个分布中采样.但是这个采样操作是不可导的,进而导致整个模型无法BP. 解决方法就是Reparametrization tricks重参数技巧.

我们首先从从均值为0,标准差为1的高斯分布中采样,再放缩平移得到Z.

这样从 到 只涉及了线性操作(平移缩放),采样操作在NN计算图之外,而 对于NN来说只是一个常数.

离散分布的采样Gumbel-softmax

Gumbel-Softmax Trick

VAE的例子是一个连续分布(正态分布)的重参数，离散分布的情况也一样，首先需要可以采样，使得离散的概率分布有意义而不是只取概率最大的值，其次需要可以计算梯度。那么怎么做到的，具体操作如下：

对于n维概率向量 ,对 对应的离散随机变量 添加Gumbel噪声，再取样

其中 是是独立同分布的标准Gumbel分布的随机变量，标准Gumbel分布的CDF为.这就是Gumbel-Max trick。可以看到由于这中间有一个argmax操作.

上述的 argmax操作是不可导的. 所以尝试用softmax来代替, 即Gumbel-Softmax Trick. 这里我们假设argmax返回的是一个one-hot向量,那么我们需要找到argmax的一个显式且光滑的逼近. 这里的 可以利用 从均匀分布中采样得到,即.

综上总体思路:

1. 基于Gumbel Distribution采样来避免不可导问题
2. 在1中引入了argmax又导致了不可导(Gumbel max)
3. 又引入softmax函数来对argmax进行光滑近似,使得可导(Gumbel softmax)

具体步骤如下:

• 对于网络输出的一个n维向量v, 生成n个服从均匀分布U(0,1)的独立样本

• 通过 计算得到

• 对应相加得到新的值向量

• 通过softmax函数

这里  就可以实现对argmax的显式且光滑的逼近

温度参数 的影响:  越小(趋近于0), 越接近categorical分布; 越大(趋近于无穷), 越接近均匀分布

img

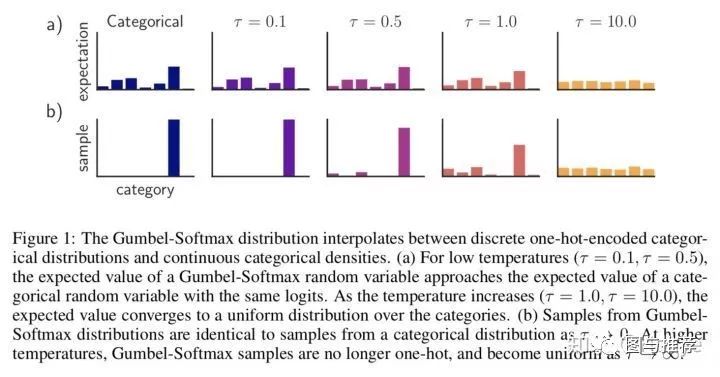
证明

常规的softmax形式为

其中, 是softmax之后得到一个概率密度函数. 那么有没有某个分布能够等价于上述的分布呢?

如果对每个 添加独立标准的gumbel噪声(位置为0,尺度为1),并选择值最大的维度输出,每次的输出结果有一个概率密度函数.这样一个概率密度同样为  .

化简

积分里面是  的gumbel分布,整个积分为1,则

结果与softmax的分布一致.

为什么需要gumbel-softmax

乍看起来，gumbel-softmax 的用处令人费解。比如上面的代码示例，直接使用 softmax，也可以达到类似的参数训练效果。但两者有着根本的区别。原理上，常规的 softmax 直接建模了一个概率分布（多项分布），基于交叉熵的训练准则使分布尽可能靠近目标分布；而 gumbel-softmax 则是对多项分布采样的一个近似。使用上，常规的有监督学习任务（分类器训练）中，直接学习输出的概率分布是自然的选择；而对于涉及采样的学习任务（VAE 隐变量采样、强化学习中对actions 集合进行采样以确定下一步的操作），gumbel-softmax 提供了一种再参数化的方法，使得模型可以以端到端的方式进行训练。

Ref

1. CATEGORICAL REPARAMETERIZATION WITH GUMBEL-SOFTMAX
2. https://zhuanlan.zhihu.com/p/35218887
3. https://casmls.github.io/general/2017/02/01/GumbelSoftmax.html
4. http://lips.cs.princeton.edu/the-gumbel-max-trick-for-discrete-distributions/
5. https://blog.csdn.net/jackytintin/article/details/53641885
6. 大量tf代码实例
7. https://www.quora.com/How-do-we-compute-the-gradient-of-a-ReLU-for-backpropagation
8. https://blog.csdn.net/jackytintin/article/details/79364490

推荐阅读

AINLP年度阅读收藏清单

薅当当羊毛的机会又！双！！叒！！！叕!!!来了

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。