数学家教你烤肉饼：按最佳时机翻面可节省近1/3烹饪时间，网友：想去汉堡王应聘厨子了

万博 发自 凹非寺
量子位 | 公众号 QbitAI

不得了！现在连烤个肉饼都需要数学加持了。

最近，一位等离子体物理学博士用三大偏微分方程中的热方程 （The Heat Equation）证明：

在烤肉的过程中，多次反转肉饼使其两面多次加热，可以加快肉饼烤制的速度，最佳策略下能节省29%的烹饪时间。

而且，翻转肉饼的最佳时机也暗藏玄机：

前几次翻转间隔时间要大概一致，而最后一次，则需要等久一点再翻面。

相关论文已上传到arXiv上。

这个方法要是被汉堡大户KFC们知道了，还不笑开花？

不仅节省燃料成本，出菜速度也提上来了，妥妥降本增效小妙招啊。

不过，也有网友表示，一般情况下我都会遵从科学指示，不过吃这件事上还是烤肉的品质更重要：

还有网友表示，想拿着这篇论文去应聘汉堡王的大厨了：

多次翻面烤肉熟得快

在此之前，科学食品作家哈罗德-麦基 （Harold McGee）已经提出：

如果在烤肉的过程中，通过多次快速翻转肉饼，就能让肉饼的两面同时加热，这种操作相比烤完一面再烤另一面的常规烹饪方式，烹饪时间更短。

但是这种猜想，并没有在理论层面进行证实。

于是，来自威斯康星大学麦迪逊分校的数学家：让-吕克-蒂菲奥特 （Jean-Luc Thiffeault），用一个基于热方程的数学模型，让这一猜想得到实锤。

整个证明过程，是这样的：

首先，蒂菲奥特设想了一个场景：

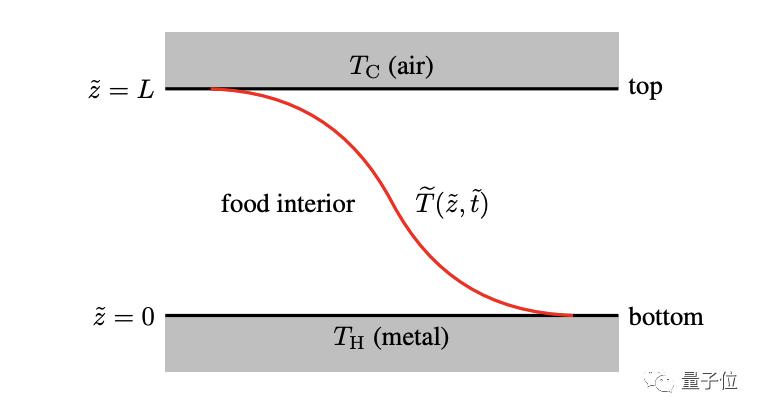
对一个厚度为1厘米，面积无限大的肉饼进行烤制，温度设定为200⁰C。

烤制过程中，肉饼的厚度设定为z˜=0到z˜=L，温度变化满足热方程Te t˜= κTez˜z˜，0 < z < L，˜ t >˜ 0。

方程的初始条件为Te(˜z, 0) = Te0(˜z)，边界设定为牛顿冷却定律− k Tez˜(0,t˜) = h˜ 0 (TH − Te(0,t˜)), k Tez˜(L,t˜) = h˜ 1 (TC − Te(L,t˜)。

（这里的热方程理论，是19世纪由约瑟夫·傅立叶提出的，主要作用是模拟热定在给定区域的扩散过程。）

当肉饼加热到70⁰C度时，证明肉饼可以出炉了。

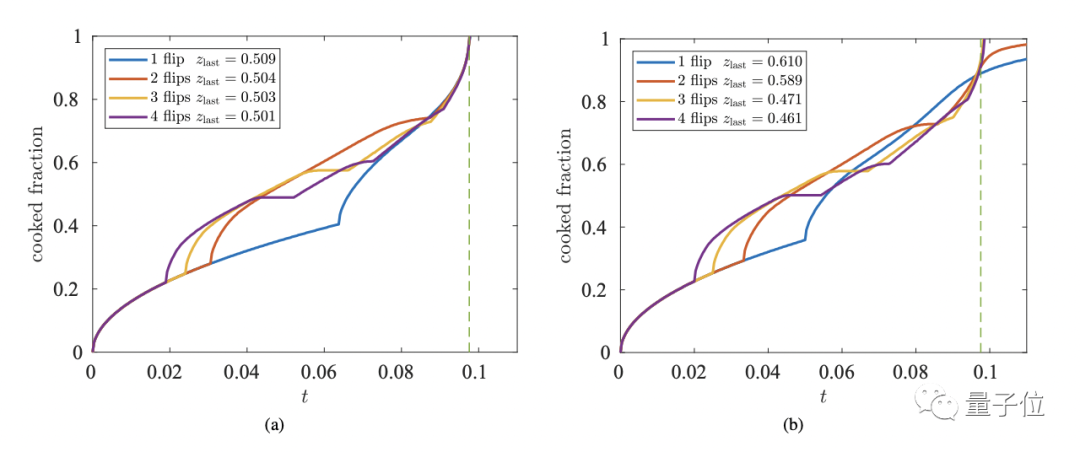
之后，在满足上述模型和设定条件下，蒂菲奥特模拟了肉饼只翻动一次和多次翻动情境下的烤制时间。

结果表明，烤制过程中多次翻动肉饼，的确可以达到类似同时双面烤制的效果，大大缩短烤制的时间。

将翻面时的受热状况用图表示出来就是这样的：

麦基的猜想得到证实，接下来的一个问题就是：

如何翻转肉饼时间才是最短的？

蒂菲奥特模拟不同的翻转次数和翻转的间隔时间，同时用数学软件MATLAB对模拟过程进行了优化。

通过不断调整翻转次数和间隔时间，蒂菲奥特有了3大发现：

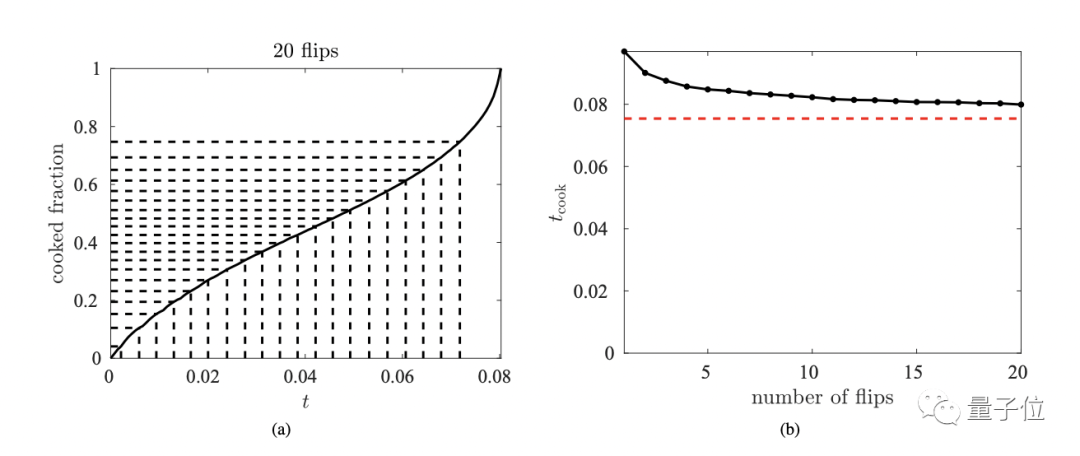
首先，在最优翻转次数——20次——情况下，最佳烹饪时间趋近于63秒，而单次翻转时间为80.5秒，相比之下可以将烤制时间减少29%。

其次，烤制时间的数值曲线表明，随着翻转次数的增加，烤制时间优化水平会逐渐收敛。

也就是说，随着翻转次数的增加，对于烤制时间的优化效应会逐渐减少，无论翻转次数如何增加，最多也只能节省29%的烤制时间。

最后，蒂菲奥特表示，烤制肉饼时翻转的间隔时间也有秘诀：

从函数曲线来看，前面若干次的翻转间隔时间应该大致相同，到了最后一次翻转时，间隔时间应该长一点，这样更有利于热量在肉饼中扩散。

总结一下就是，想要烤肉熟得快，翻个20次也就够了，最后一次翻转的时候，记得时间间隔长一点。

各位看官，学会了吗？

论文作者介绍

这位教人烤肉的数学家让-吕克-蒂菲奥特 （Jean-Luc Thiffeault），等离子体物理学博士，现任威斯康星大学麦迪逊分校的应用数学教授。

研究领域主要涉及应用数学以及流体动力学等。

迄今为止，在相关领域发表155部著作，被引用超过2500次。

参考链接：

[1]https://arxiv.org/pdf/2206.13900.pdf
[2]https://www.discovermagazine.com/the-sciences/how-mathematics-solved-the-burger-flipping-problem

— 完 —

「人工智能」、「智能汽车」微信社群邀你加入！

欢迎关注人工智能、智能汽车的小伙伴们加入我们，与AI从业者交流、切磋，不错过最新行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~