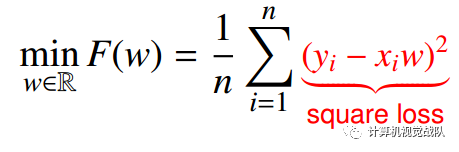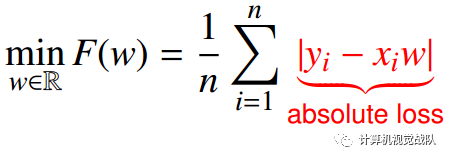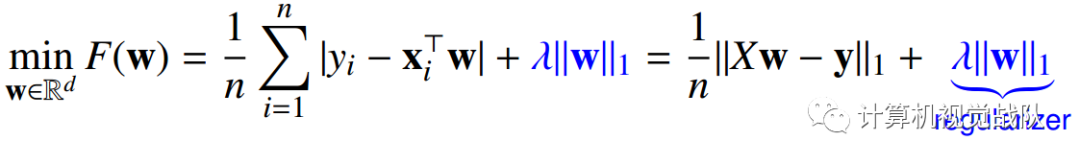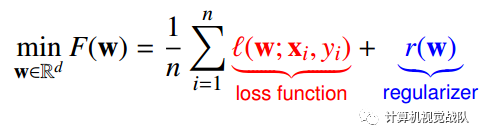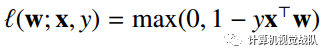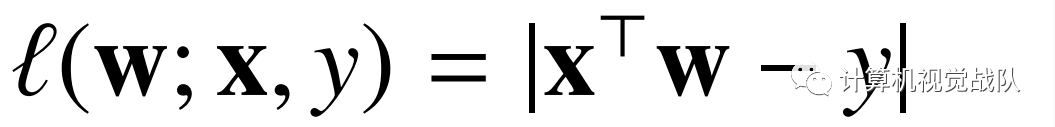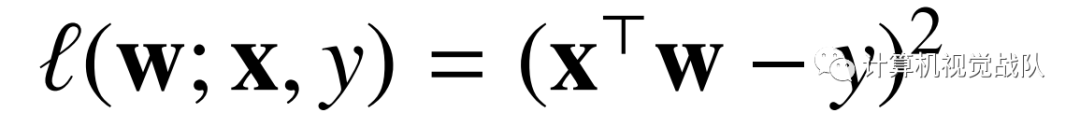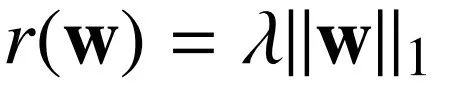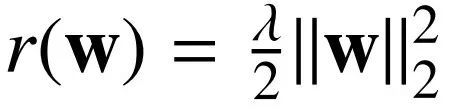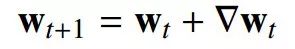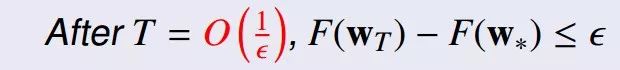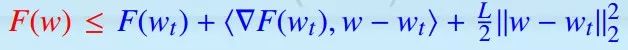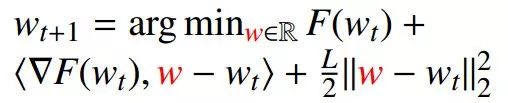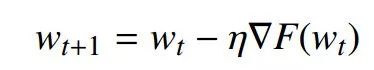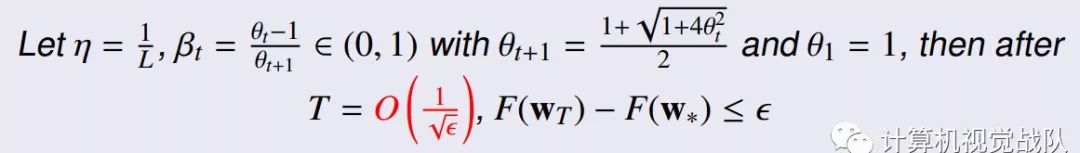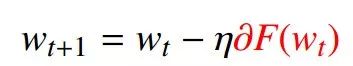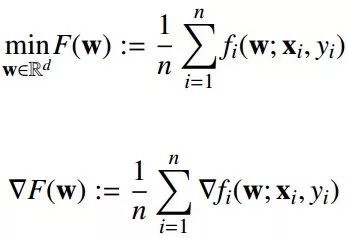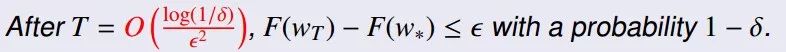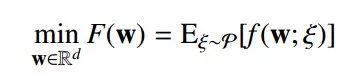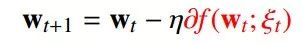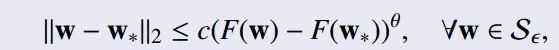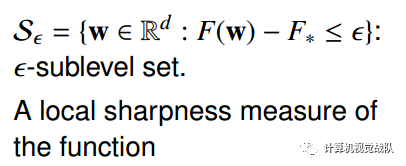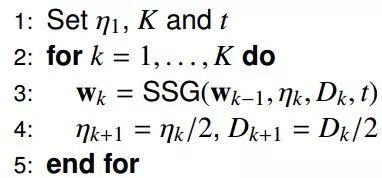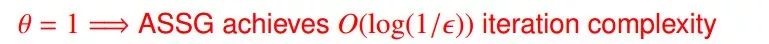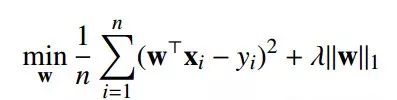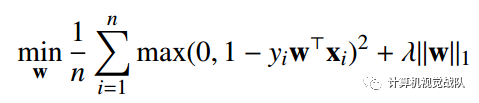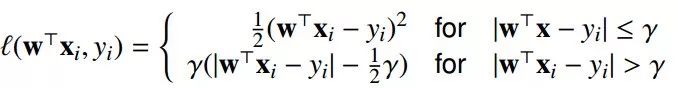在局部误差边界条件下的随机子梯度方法的加速
今天我们主要针对Stochastic Subgradient Methods来进行详细讲解,如果有兴趣的读者,进认真和我们一起阅读下去,记得拿好纸和笔~
首先,简单通过机器学习的例子来引入今天的话题。
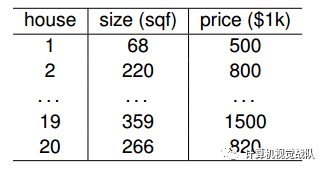
上表是某地区的房屋售价数据。
线性模型如下:
y=f(w)=xw
其中,y表示价格,x表示大小。
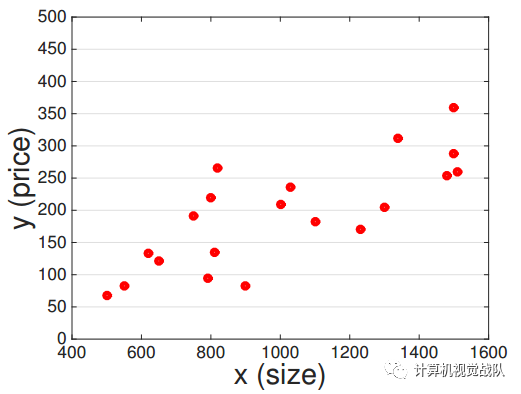
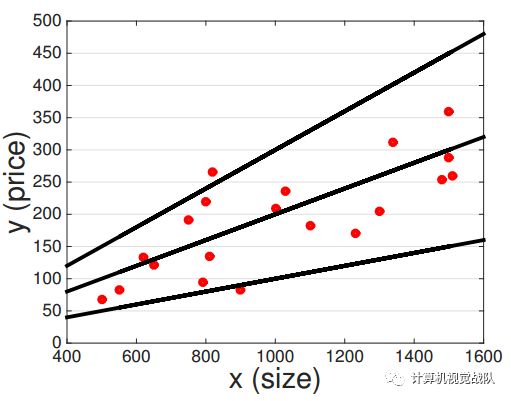
可以拟合出一条上图的数据,但是到底哪个函数最好呢?
其实这是机器学习的入门知识,会的人应该在脑海中立马有了自己的函数构架了。
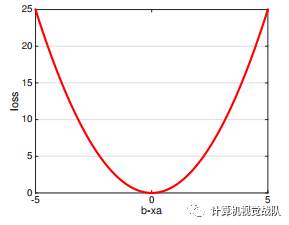
通过最小二乘回归:
square loss具有平滑性。
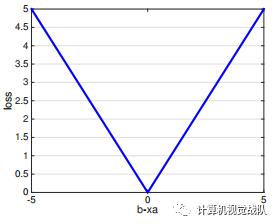
如果是最小绝对偏差:
absolute loss 不具有平滑性。
还有,用高维模型的话,如下:
最后一项是正则项。
绝对损失对离群值问题更有鲁棒性;
L1-Norm正则项,大家应该都知道,可以用于特征选择。
则机器学习的问题就如下所示:
对于分类、回归和正则项来说,有如下方式:
分类:铰链损失
回归:平方损失和绝对损失
平方损失:
绝对损失:
正则项:L1-Norm和L2-Norm
L1-Norm:
L2-Norm:
凸优化问题
其中,Rd→R是凸的,最优值为:
最优解为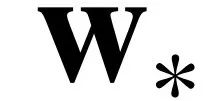
最终目的就是找到最优解:
其中:
复杂性量度
大多数优化算法都是通过迭代计算得到的:
迭代复杂度:迭代次数T(ε)为:
其中0<ε≤1。
时间复杂度:T(ε)*C(n,d),C(n,d)就是每次迭代的成本。
现在开始我们正式进入主题:
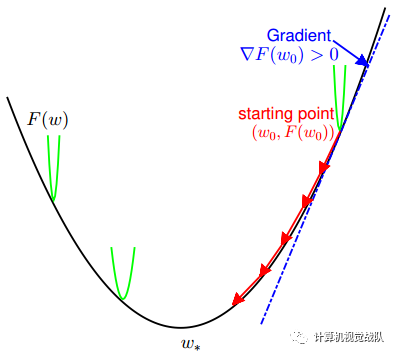
梯度下降(GD)
定理主要来自于:Yurii Nesterov. Introductory lectures on convex optimization : a basic course. Applied optimization. Kluwer Academic Publ., 2004. ISBN 1-4020-7553-7.
问题依然是:
(平滑)
迭代:
GD:
步长:η=1/L,且η>0。
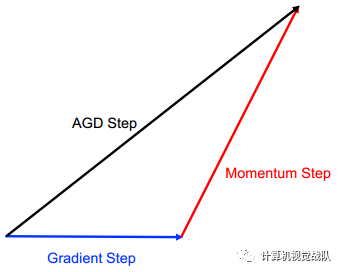
加速梯度下降法
其中,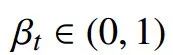
定理参考于:Arkadi Nemirovski, Anatoli Juditsky, Guanghui Lan, and Alexander Shapiro. Robust stochastic approximation approach to stochastic programming. SIAM Journal on Optimization, 19:1574–1609, 2009
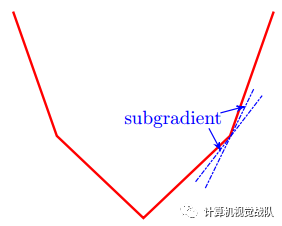
次子度下降(SG)
其为非平滑的。
时间复杂度
其中,在计算梯度的时候很费时。
如果对于大数据的时候,d和n都特别大,要计算梯度,需要通过所有数据点,每个迭代步骤,都需要这样计算。
所以出现了随机梯度下降算法(SGD):
随机子梯度下降(SSG)
迭代:
时间复杂度:
怎么加速呢?
Y. Xu, Q. Lin, and T. Yang. Stochastic convex optimization: Faster local growth implies faster global convergence. In ICML, pages 3821-3830, 2017
局部误差边界约束条件下的快速全局收敛性,用于机器系学习。
局部误差边界条件(LEB)
定义:有一个常数c>0,还有一个局部增长率θ∈(0,1],则:
则F(W)满足局部误差边界条件。
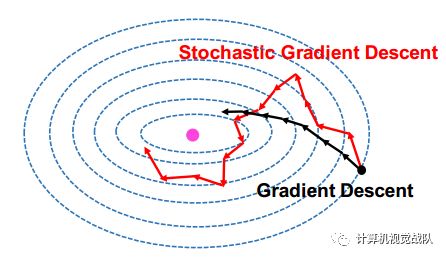
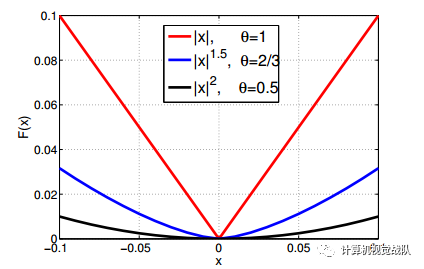
从下图中可以清楚看出加速的效果:
主要的步骤如下:
其中:
然后再来看看时间复杂度:
实验
鲁棒回归:
稀疏分类:
最小二乘+L1-Norm:
平方铰链损失:
Hurbe损失:
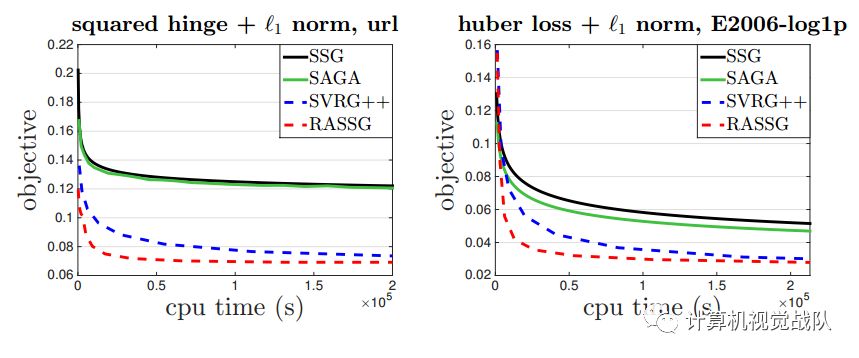
实验结果:
欢迎加入我们“计算机视觉战队”!!!