多导弹协同制导研究综述

2018 年 3 月 6 日 无人机

本文作者：赵建博，杨树兴（北京理工大学宇航学院）

摘要：综述了多弹协同制导领域的主要研究成果和国内外的最新进展，简述了其发展历程。鉴于现有的协同制导研究成果绝大多数主要涉及时间协同问题，而且开环的时间协同制导律已经得到了很好的综述，因此重点综述了闭环的时间协同制导律。按照协同制导架构，多弹时间协同制导可划分为双层协同制导架构和“领弹－从弹”协同制导架构；按照导弹间通信的拓扑结构还可分为集中式和分布式。首先综述了两种协同制导架构，即双层协同制导架构和“领弹－从弹”协同制导架构，并对这两种架构进行了讨论和比较；其次分别综述了集中式和分布式多导弹协同制导的研究成果，分析了这些多导弹协同制导方法的优缺点，并对该研究领域的重要发展方向进行了展望。

关键词：多导弹；导弹制导；协同制导；通信；双层协同；领弹－从弹；齐射攻击；攻击时间

随着反导弹技术的发展，多导弹协同攻击和防御以其特有的优势正在受到越来越多的关注，而多弹协同制导作为保证攻击和防御性能的关键技术也得到了快速发展。首先，在进攻方面，多弹协同制导可以通过弹群协同，将多枚导弹融合成一个信息共享、功能互补、战术协同的作战群体，利用群体优势对敌防御体系和目标进行多层次、全方位的打击，实现突防能力的整体提升［1］。其次，多枚导弹还能够完成单枚导弹不易完成的任务［2］，例如：实现饱和攻击与“侦查－打击－评估”一体化协同作战［3］。第三，弹群中导弹可采用不同的制导体制，从而实现战术隐身、增强电子对抗和对目标的识别能力、提升复杂战场环境下的抗干扰能力等［4］。此外，也可通过弹群中的部分导弹带有价格昂贵的导引头，其他导弹仅带有低成本的制导控制部件，以降低作战成本、提高效费比等。在防御方面，通过多弹协同也可以提升反导系统的效能［5］。当前，各国均已认识到多导弹协同攻击和防御的重要性，并在积极研制相关型号的导弹系统，例如：俄罗斯研制的П－700花岗岩超声速反舰导弹和美国正在研制的网火作战系统等［6］，而用以实现多导弹协同攻击和防御的协同制导问题也正逐渐成为一个研究热点。与之类似的无人机编队协同控制问题经过多年的研究已经有了一定的研究成果，但因为导弹具有其特殊性，无人机的相关研究成果并不能直接应用于导弹的协同制导。事实上，导弹协同制导是多智能体协同控制的一个重要方面，但与无人机和智能体相比，导弹的运动速度更高，使得多导弹协同控制方法的实时性要求更高、通信量更小；另外导弹难以实现无人机和智能体的盘旋、静止，且其弹道应尽可能平直，避免过多的转弯［7］，这就对其协同提出了更高的要求。

多导弹协同攻击研究源于突防的需求，林涛等［8］在2005年系统地阐述了其研究意义、作战样式和实施条件。Jeon等［9］在2006年首次将时间约束引入到导引律的设计中。在此基础上，赵世钰和周锐［7］在2008年提出一种可适用于集中式和分布式通信拓扑的双层协同制导架构，首次通过导弹间的信息交流实现协同制导。张友安等［10］在2009年首次将“Leader－Follower”编队控制方式应用到多导弹协同制导中，并提出一种“领弹－从弹”协同制导架构。此后，关于协同制导方法的研究均是在以上两种协同制导架构的基础上展开。

目前，仅检索到3篇关于多导弹协同制导方法的综述性文献。王建青等［2］总结了带有弹着时间约束、终端角度约束、弹着时间与终端角度同时约束和终端速度约束的制导律，但均为开环式协同制导律。肖增博等［11］总结了部分2011年以前的基于攻击时间和攻击角度约束的协同制导规律，但也主要介绍的是开环协同制导律。张友安等［12］将部分闭环式协同制导律分成4类进行综述，但这4种类型之间具有重叠部分，且有一些开环协同制导律也被包含在闭环协同制导律中加以介绍。

事实上，实现多导弹协同制导的核心是通信，根据在线或离线信息交互，多导弹协同制导方法可以分为开环式与闭环式两类。所谓开环式协同制导指的是在导弹编队发射前已经人为设定了对每枚导弹的期望值。飞行过程中，导弹之间不存在信息的交流。与之相反，闭环式协同制导中导弹无需预先设定对每枚导弹的期望值，导弹的协同攻击通过导弹间的信息交流来实现。对于开环式协同制导，如果将协同目标定义为时间上的协同，则为了实现攻击时间的限制，可采用各种导引与控制方法，其中包括：偏置比例导引［9，13－14］、滑模控制［15－17］、最优控制［18］、微分对策［19］和动态面控制理论［20］等。关于开环式时间协同制导方法的相关综述可以参考单枚导弹带有时间约束导引律的综述［21］。而且，在一般意义上，预先设定攻击时间的制导方案并不能被看成是真正的多弹协同制导［22］。因此，对于攻击时间的协同，本文仅涉及闭环式协同制导方法，并将其简称为协同制导方法。对于闭环式协同制导，导弹之间的通讯是关键，如果不能通讯就不可能实现闭环式协同制导。导弹之间通讯的拓扑结构主要包括集中式通讯和分布式通讯两种。集中式通信拓扑是指在导弹集群中存在一枚或多枚导弹能够与所有导弹进行信息的交流，而分布式通讯是指导弹集群中的导弹仅能与若干枚与其相邻导弹进行信息的交流。因此，根据弹群中导弹之间的通讯拓扑可以将多弹协同制导方法分为集中式和分布式协同制导两类，进而还可以根据上述两种协同制导架构进行分类。

通过对现有协同制导方法的相关文献进行检索可以发现，绝大多数的文献都将“协同”定义为时间的协同。因此，在本文的文献综述部分仅涉及时间协同的制导研究成果。本文首先分析介绍了两种协同制导架构。其次，通过归纳总结国内外已有的关于多导弹协同制导方法的主要研究成果，从采用集中式和分布式通信拓扑结构的两类协同制导问题出发，对基于两种协同制导架构的制导方法分别进行综述，并在此基础上对该方面值得研究的重要问题和发展方向进行了展望。

1 协同制导架构

现有的众多协同制导方法均是在双层协同制导架构和“领弹－从弹”协同制导架构的基础上开展的研究。前者可以同时应用于同构导弹集群和异构导弹集群的协同制导，而后者是专门为更有应用前景的异构导弹集群而设计的。这两种协同制导架构的提出是基于导弹的运动学特性和对攻击协同的要求，故均可以实现多导弹的协同制导。

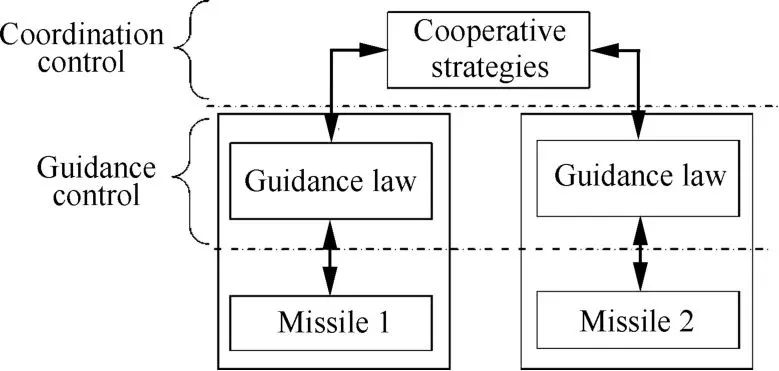
双层协同制导架构由赵世钰和周锐［7］于2008年提出，其以满足导弹飞行特点的带约束导引律为底层导引控制、以包含协调变量的集中式或分散式协调策略为上层协调控制（见图1［11］）。其中，协调变量指的是实现一种协同任务所需的数量最少的信息，而通过协调函数可以确定协调变量的取值，即期望的协调变量［23］。然而，除了文献［7，24］是利用协调函数来确定协调变量的取值外，其余均是直接定义期望的协调变量。这种协同制导架构的协调策略指的是通过控制导弹的弹道从而使每枚导弹的协调变量逐渐趋近于期望的协调变量，从而实现协同制导。这种协同制导架构既保证了导弹能够命中目标，又满足了协同攻击的要求，而且针对不同的协同任务，可以选择相应的制导律和协调策略，具有一定的通用性。

图1 双层协同制导架构［11］
Fig．1 Two－level cooperative guidance framework［11］

“领弹－从弹”协同制导架构由张友安等［10］于2009年提出。这种架构是根据协同要求选择导弹的参考运动状态，并将领弹的作为期望参考运动状态。通过对领弹或相邻导弹参考运动状态的跟踪，从弹的参考运动状态逐渐趋于期望值，从而实现多导弹协同制导。在这种协同制导架构中，领弹可采用一般导引律，运动状态不受从弹影响，而领弹又有着不同的选择，其中包括了以导弹集群中的一枚导弹作为领弹［5，10，22，25－31］，以目标作为领弹［32－34］，以及以虚拟点作为领弹［10］3 种情况。这种协同制导架构可以认为是双层协同制导架构的一种变形，即以参考运动状态作为协调变量，以领弹的参考运动状态作为期望的协调变量。然而，相比于双层协同制导架构，这种协同制导架构的领弹不受其余导弹的影响，而且可以采用误差控制的方法作为底层导引控制。若领弹采用比例导引，则选择当所有导弹都采用经典比例导引飞行时，待飞时间最长的作为领弹。虽然这种协同制导架构需要提前确定领弹，且由于领弹的重要地位使得协同系统的可靠性和鲁棒性较差，但相比于双层协同制导架构具有信息的实时性较好、更加有利于导弹集群的扩展等优点，而且采用这种协同制导架构的制导方法由于使用了相对成熟的控制理论，所以在稳定性证明上相比于前一种更为简单。

2 集中式协同制导

集中式的通信拓扑结构，具有一个或几个中心节点掌握弹群的全部信息，更有利于做出最优的决策。若采用双层协同制导架构，则可以迅速计算出期望协调变量；若采用“领弹－从弹”协同制导架构，则从弹的参考运动状态可以更快收敛于领弹。然而，集中式通信拓扑也存在鲁棒性差、通信代价高、不利于扩展等缺陷［35］。

2．1 集中式双层协同制导方法

对于集中式的双层协同制导方式，会存在一个集中式协调单元，即所有导弹将协调所必需的状态信息传送给集中式协调单元，该单元直接计算出期望的协调变量值，然后将其广播至所有导弹。这种集中式协调单元可以只存在于一枚导弹中，也可以分布于所有导弹中。如果只存在于一枚导弹中，则导弹集群的总计算量要小很多，通信拓扑结构简单，利于导弹集群的扩展，但由于集中式协调单元的失效将致使整个系统的协调控制失败，所以存在系统的可靠性、抗毁性和鲁棒性差的问题。若将集中式协调单元分布于所有导弹中，则情况与之相反。

2．1．1 协调单元只存在于一枚导弹中

对于这类协同制导方法，现有的研究成果均是以导弹的剩余时间作为协调变量，以全体导弹剩余时间的（广义加权）平均值作为期望协调变量，而底层导引律可分别采用偏置比例导引律［7，36－37］或基于滑模控制的导引律［24，38］。

针对平面内多导弹同时攻击静止目标的协同制导问题，赵世钰和周锐［7］设计了一种以带有时间约束的偏置比例导引律［9］为底层导引控制，以导弹剩余时间为协调变量的双层协同制导律。其中，取所有导弹控制能量之和为协调函数，并根据使协调函数达到最小值来确定期望协调变量的取值，即导弹剩余时间估计值的广义加权平均数。虽然偏置项的系数是为了保证控制能量最优，但由于弹目距离出现在分母项，则当导弹向目标靠近时，需用过载可能会超出可用过载的限制，而且期望剩余时间可能无法保证大于或者等于所有导弹进行比例导引飞行时的剩余时间最大值，与文献［9］提出的先决条件相违背。此外，文献［39］在文献［7］的基础上，将上层协调策略替换成一致性算法，将攻击时间一致性问题转化为分歧系统的稳定性问题，并利用李雅普诺夫函数的方法得出在固定和时变通信拓扑结构下、同时存在通信时延及拓扑结构不确定的攻击时间一致性收敛问题的线性矩阵不等式判据。

针对文献［7］存在的问题，Zhao和Zhou［36］对于平面内的静止目标依然以导弹剩余时间为协调变量，并将其作为偏置项的控制部分设计了一种偏置比例协同导引律。其中，期望的协调变量采用全体导弹剩余时间的平均值。这种协同制导律在偏置项系数中用导弹初始状态对偏置项进行了单位化，而且当导弹向目标靠近时，协同制导律逐渐趋近于比例导引，但导弹的初始状态将影响协同效果，且没有对过载进行优化。同时，通过采用针对机动目标的比例导引律［40］和将文献［41］所介绍的剩余时间估计方法针对机动目标进行修正，可将上述方法拓展到同时攻击机动目标的情况。针对三维空间的协同制导问题，如果采用三维比例导引律［42］，可通过相关运动学关系将上述方法拓展到三维空间［37］。为了能够实现全局控制能量最优，Kumar和Ghose［24］对于平面内的静止目标设计了一种以基于滑模控制的时间约束导引律［16］为底层导引控制，上层协调控制以所有导弹的滑模面偏差量总和最小为依据，得到期望攻击时间为剩余时间平均值的协同制导方法。这种协同制导方法虽然实现了全局控制能量最优，但由于采用了滑模控制，过载表达式过于复杂且会出现抖振的现象。

对于平面内需要限制视线角且同时攻击静止目标的协同制导问题，张保峰等［38］将导弹剩余时间的平均值作为期望协调变量，通过滑模控制分别设计了带有时间约束和带有视线角约束的两种导引律，并将它们通过切换策略进行结合，实现了具有角度约束的协同制导，但这种方法仅适用于导弹剩余时间差异不大的情况，且由于使用了滑模控制，使得过载表达式较复杂，会出现抖振的情况。

2．1．2 协调单元分布于所有导弹中

对于这类协同制导方法，期望的协调变量大多是采用其余导弹剩余时间的平均值，而底层导引律可采用变系数比例导引律［41］、偏置比例导引律［43－44］和最优导引律［45］以实现协同制导。

Jeon等［41］针对平面内的静止目标，提出了一种导引系数只根据导弹的弹目距离和相对剩余时间误差（其余导弹剩余时间均值与导弹剩余时间之差）来调整，使得导弹集群剩余时间方差为零的变系数比例导引协同制导方法。这种协同制导方法可以应用于集群中导弹速度不同的情况。但与比例导引律相比，这种协同导引律的过载在制导初期要大很多，有可能会超出导弹的过载限制。为了使导弹集群既能在平面内同时攻击机动目标又能保证集群所需能量总和最小，基于单枚导弹的最优导引律［46］，Sun和 Xia［45］分别考虑了导弹过载是否需要垂直于速度方向和长／短距离制导具有不同剩余时间求解方法的情况，通过重新定义代价函数和哈密顿变量使其包含全部导弹的相关信息，提出了一种协同最优导引律。其中，协同导引律所需的导引系数采用文献［41］所提出的方法求解。与文献［41］相比，这种协同制导方法虽然具有导弹集群所需总能量最小且能适用于机动目标的优点，但仍不能保证导弹需用过载小于可用过载，且通过仿真只证明了这种协同导引律可应用于具有固定速度的目标，而且对于速度的大小和方向均有限制。

同样，为了实现对平面内静止目标的协同打击，Wu等［43］设计了一种将文献［41］所定义的相对剩余时间误差应用到偏置项中的偏置比例协同导引律，并发现了信息更新速率对剩余时间方差收敛的影响。为了减小导弹在中／末制导交接区域内的法向过载，往往要限制弹道角。因此，对于三维空间内的静止目标，在竖直平面内，末制导采用比例导引律，而在水平平面内，在中／末制导均采用上述偏置比例协同导引律的基础上，在中制导中加入相比于弹道偏角更易测得的偏航角误差控制项，以便能够同时实现角度控制与协同打击。此外，这种方法还可以应用于多个导弹集群的协同攻击，并可通过调节中／末制导的交接位置实现集群间的碰撞角协同。在上述偏置比例协同导引律的基础上，Zeng等［44］将偏置项系数中的前置角正弦值换成了弹目距离的倒数，并保留前置角的符号，亦实现了协同制导。这种方法虽然避免了求解前置角的正弦值，减小了弹载计算机的计算量，但由于弹目距离出现在分母的位置，当导弹足够接近目标时，就需要采用比例导引法，而需要变换导引律的弹目距离临界值往往要通过工程经验得出，不利于应用。

2．2 集中式“领弹－从弹”协同制导方法

对于采用集中式通信拓扑的“领弹－从弹”协同制导方式，领弹与所有从弹均有信息交流，而从弹之间不存在信息交流。这类协同制导方法大多采用弹目距离和弹道前置角或者是剩余时间作为从弹的参考运动状态，而从弹的跟踪方式可以采用偏置比例导引［10，22，31］、增广比例导引［27］和最优导引律［26］等方法。

针对平面内的静止目标，张友安等［10］设计了一种领弹采用比例导引，而从弹采用比例导引与机动控制相结合的协同制导律。先以领弹的弹目距离和弹道前置角作为期望参考运动状态建立了从弹的运动状态跟踪系统。然后，针对此系统，采用时标分离的方法设计了关于期望参考运动状态的快子系统和慢子系统，并对这两个系统分别进行动态逆的控制设计，得到从弹的机动控制指令。如果为每一枚领弹引入一个与之速度相同的虚拟领弹且将领弹速度也传递给从弹，则可将此协同制导方法推广到从弹速度不同的情况。这种协同制导方法首次将“领弹－从弹”协同制导架构引入到导弹的协同制导问题中，但从弹的过载表达式过于复杂，对弹载计算机的要求过高。针对这个问题，Zhao等［22］对于平面内的静止目标，设计了一种领弹采用比例导引，从弹采用文献［9］所介绍的带时间约束的导引律且期望剩余时间为领弹剩余时间的协同制导律，并且针对从弹不具备导引头的要求，为从弹设计了一种弹目视线角速率的计算方法。对于平面内的机动目标，Zhao等［31］在文献［10］的基础上，为了保证领弹的弹目距离总是大于从弹的，设计了一种基于领弹剩余时间的期望慢子系统带宽的自适应变化规律，从而实现了协同制导。

对于三维空间内的协同制导问题，马国欣等［27］针对导弹速度不同且目标静止的情况，设计了一种领弹在俯仰和偏航两个通道均采用增广比例导引［47］，而从弹在俯仰通道上采用增广比例导引，偏航通道采用机动控制的三维协同制导律。俯仰通道上的增广比例导引使领弹与从弹在该通道上的前置角逐渐趋于零，即弹道完全落到偏航面内，而从弹的机动控制采用动态逆的方法设计，使从弹与领弹在偏航面内的弹道曲率（相对于速度）趋于一致，从而达到时间协同。针对三维空间内的机动目标，王晓芳等［26］以目标为球心，以领弹距目标的距离为半径构造虚拟球体。在虚拟球体上确定虚拟点且使虚拟点和目标连线的方向为从弹的理想攻击方向。在领弹采用比例导引的情况下，设计了最优控制器控制从弹的速度和弹道角，使其在控制能量最优的条件下逼近虚拟点，并对虚拟点的轨迹进行了优化以减小从弹的需用过载。这种协同制导方法既保证了同时攻击，又限制了从弹的攻击角度，但其只给出了从弹关于速度和弹道角的指令，不利于应用。

3 分布式协同制导

由于在实际的战场上很难保证弹群中导弹间的集中式通信，因此往往采用分布式的通信拓扑结构，即每枚导弹只能与其相邻导弹进行信息交流，且通过图论中的加权拉普拉斯矩阵来描述各导弹间的通信关系。这种通信拓扑结构虽然避免了集中式通信拓扑所存在的问题，但却使得从弹趋于期望协调变量和参考运动状态的时间是无穷的，而且系统的可靠性较差。虽然部分采用分布式通信拓扑的协同制导方法可以通过改变加权拉普拉斯矩阵在双层协同制导架构和“领弹－从弹”协同制导架构间转换［48］，但这种现象仍缺乏普适性证明。所以对于分布式协同制导方法，仍可按照两种协同制导架构来进行分类。

3．1 分布式双层协同制导方法

对于采用分布式通信拓扑的双层协同制导方式，虽然可以利用协调一致算法将已得到的集中式协调策略进行分散化设计，直接得到分散式协调策略［7］，但依靠一致性算法获得各导弹期望剩余时间的方法都面临一个共同的问题，即各导弹期望剩余时间的收敛依赖于实际剩余时间，而各导弹又通过控制作用使实际剩余时间向期望剩余时间收敛。换言之，期望剩余时间的收敛与实际剩余时间的收敛互为前提，系统的稳定性不能得到保证［49］。这类协同制导方法大多采用导弹剩余时间作为协调变量，偏置比例导引［36，48－53］、增广比例导引［54］、变系数比例导引［55－56］和最优导引律［57］作为底层导引控制以实现协同制导。

针对平面内的静止目标，Zhao和Zhou［50］在文献［7］的基础上，给出了基于一致性算法，将集中式的期望协调变量——导弹剩余时间估计值的广义加权平均数离散化后应用到分布式协同制导的过程。彭琛等［35］在此基础上通过对平衡的强连通有向图进行镜像运算以及为不一致性动态系统定义合适的李雅普诺夫函数等，证明了跳变网络拓扑条件下采用加权一致算法可以实现导弹的协同制导，并得到指数收敛速度下限。此收敛速度可以作为指定实际解算过程中收敛周期的依据。考虑到文献［50］需要通过数值的方法求出导弹的期望剩余时间，从而无法得出导弹法向过载的解析表达式。Park等［52］在一般质点运动学方程的基础上，同样根据一致性原理，分别以剩余距离和剩余时间作为协调变量来设计协同导引控制项，并以此作为偏置比例导引的偏置项以实现协同制导。这种协同制导方法由于采用了一般质点运动学方程，虽然能同时应用于导弹和无人机，但却无法保证导弹能够命中目标，且文中也并没有给出相关证明。为解决文献［50］存在与文献［9］提出的先决条件相违背的情况，Hou等［51］针对平面内的静止目标，在文献［9］的基础上，对于固定的强连接通信拓扑结构，将期望的协调变量选为自身和相邻导弹剩余时间中的最大值，而对于时变的强连接通信拓扑结构，导弹选择拓扑结构改变前和改变后的剩余时间中的较大值作为自身的剩余时间参与比较。这种协同制导方法对于弹载计算机和通讯设备的要求最低，但飞行时间较长，而且仅适用于各枚导弹剩余距离比较接近的情况。

除了针对文献［50］所设计的协同制导方法存在的不足进行改进外，还有一些协同制导方法将适用范围拓展到机动目标、三维空间和目标发射电磁干扰等情况。对于平面内的机动目标，Zhao和Zhou［36］在集中式协同制导律的基础上，将期望的协调变量选为在可通信范围内所有导弹剩余时间的平均值，实现了协同制导，但文中并没有对全体导弹剩余时间误差的收敛性给出相关证明。针对这个问题，孙雪娇等［54］对于平面内的机动目标设计了一种由增广比例导引［40］和分布式协调策略组成的协同制导律，即在增广比例导引闭环运动学方程的基础上，基于一致性原理设计了以弹目距离和导弹前置角为协调变量的多导弹协同制导律，并由此得出导弹切向与法向过载。这种协同制导方法因为需要实时改变导弹的切向过载，对导弹的发动机设计提出了很高的要求。在三维空间内，Daughtery和Qu［57］以导弹相对于目标的距离和速度为协调变量，基于最优协同控制方法和协同剩余时间估计方法设计了使所需控制能量最优的协同导引律。文中采用时变拓扑结构的分布式通信方法，且导弹间通过传递自身的状态量和剩余时间的估计值实现了协同制导，但这种协同制导方法由于没有考虑导弹的运动学方程，无法给出导弹的过载表达式，不利于应用。为了能得到导弹的过载指令，Wei等［56］针对三维空间内的静止目标，在导弹间通信拓扑强连接的情况下，基于包含两个极限学习机的专家系统找到了导弹剩余时间与比例导引系数的关系，从而通过调整比例导引系数使得导弹的剩余时间趋近于与其通信导弹中的最大值，实现了协同攻击。然而，这种协同制导方法无法得到一般性的解析结果，不利于对其性能的分析。考虑到目标发射的电磁干扰可能会使导弹集群的通信拓扑结构发生随机变化，而且会使导弹间传输的信号出现噪声。为此，Song等［53］对于平面内的静止目标，在文献［9］的基础上去掉了偏置项系数，并设计了一种时间离散的期望剩余时间的表达式。通过确定合适的表达式系数，使得在拓扑结构循环的条件下协同系统的协方差稳定系数小于1，即实现了系统的协方差稳定，从而当目标发射电磁干扰时，导弹集群仍能实现协同攻击，但由于计算量过大，这种协同制导方法仅适用于导弹数量相对较少且通信连接度低的情况。

为了满足过载限制，Hou等［55］对于平面内的静止目标将剩余时间方差为零作为协同目标，设计了一种可在有限时间内实现协同的变系数比例导引律。在此基础上，基于开关控制算法实现了过载限制，并通过顺序法实现了导弹间的分布式通信。对于平面内需要限制碰撞角且同时攻击静止目标的协同制导问题，Wang等［48］在带碰撞角约束的偏置比例导引律［58］的基础上，以剩余时间为协调变量，设计了可以实现碰撞角约束的协同偏置比例导引律。因为协同控制项与通信拓扑矩阵有关，文中还给出了为了实现协同，节点同构或异构通信拓扑应满足的充分条件。同时，此方法也适用于时变拓扑结构，并分别对可能出现的过载超出限制、领弹被孤立和存在抖振的情况进行了一些改进。为了避免使用一致性算法，马国欣和张友安［49］针对平面内的静止目标提出一种以直接互调各导弹的剩余时间差为手段，实现网络拓扑跳变条件下的多导弹同时攻击以及定序攻击的协同制导方法，即在通信网络强连通的条件下，基于文献［9，59］所提出的两种带有时间约束的导引律，并根据协同控制理论［60］分别设计了用于实现时间协同的有／无碰撞角约束的协同制导律。通过在剩余时间中加入预定偏置量，可以在同时攻击的基础上实现定序攻击。这种协同制导律由于没有采用一致性算法，有效地避免了由于中间量引入而出现的收敛耦合问题。

3．2 分布式“领弹－从弹”协同制导方法

对于采用分布式通信拓扑的“领弹－从弹”协同制导方式，领弹仅与相邻从弹之间存在有向信息交流，同时从弹也与相邻从弹之间存在信息交流。这类协同制导方法大多采用弹目距离和弹道前置角或者是导弹的位置作为从弹的参考运动状态，而从弹的跟踪方式可以采用基于一致性原理的偏置比例导引律［25，30］或指令跟踪算法［5，28，32－34］以实现协同制导。

针对二维平面内的静止目标，邹丽等［25］设计了一种领弹采用比例导引而从弹采用比例导引叠加分布式协同控制分量的协同制导方法，即以相邻导弹的弹目距离和弹道前置角作为参考运动状态，并且基于非线性系统的一阶一致性原理，设计了分布式协同制导分量。根据从弹飞行状态收敛于领弹的收敛条件，选择合适的通信加权值使协同制导系统收敛，从而实现协同制导，但这种制导方法只给出了前置角与剩余距离的指令，不利于应用。为了能够实现多个导弹编队的协同攻击，邹丽等［30］将文献［50］所设计的协同导引律扩展到了多目标／多导弹编队的协同攻击问题。导弹编队间通过各编队通信拓扑生成树的根节点进行通信。通过互相传递期望剩余时间，不同编队之间得以实现协同攻击。

除了将导弹作为质点运动学模型提出协同制导方法外，部分学者也开展了考虑导弹动力学特性的协同制导方法研究。与将导弹作为质点的协同制导方法相比，这类方法更为贴近工程实际，尤其是对于驾驶仪动态响应品质不能达到足以忽略的情况，应用范围更宽。当然，其设计过程也更加复杂。孙雪娇等［32］针对三维空间的机动目标，将目标作为领弹，基于一致性原理求出的速度矢量作为参考运动状态，并根据运动学关系，将参考运动状态转化为速度和弹道角指令，从而可以利用切换控制方法设计从弹的自动驾驶仪以跟踪速度与弹道角指令。这种协同制导算法是首次将目标作为领弹，但由于本质上是一种位置的协同算法，有可能导致导弹之间的相互碰撞，而且算法的提出基于导弹速度可控，这在实际应用中不易实现。为了能够实现对外部干扰的补偿，周锐等［33］在此基础上，基于导弹动力学系统和反步法将导弹控制系统转化为3个子系统，分别用滑模控制的方法实现了对参考运动状态的跟踪，并利用扩展状态观测器对干扰进行了估计并在控制中进行补偿。由于这种协同制导方法使用了滑模控制，不可避免会出现抖振的现象。针对这个问题和导弹间可能发生的碰撞，后德龙等［34］在文献［32］基础上，为实现碰撞自规避引入了带安全距离的同步算法，并采用动态逆控制解决了速度跟踪问题，采用基于改进微分器的抗干扰动态面控制解决了存在外部干扰的弹道角跟踪问题，从而实现协同制导。这种协同制导方法所使用的微分器与干扰观测器想比，可以估计更多的信号。

以上3种协同制导方法本质上是一种追踪导引法，即不论导弹从哪个方向发射，都要绕到目标的正后方命中，使得导弹弹道较为弯曲，对过载要求较高，而且没有给出导弹的过载指令，不利于应用。针对这些问题，赵启伦等［5］对于平面内的高超声速目标设计了一种领弹采用改进比例导引［40］，未配备导引头的从弹采用二阶一致性跟踪算法对位移和速度矢量进行跟踪的协同导引律，并且给出了协同制导律在固定通信拓扑与切换通信拓扑下成立的充分条件。这种协同制导律不需要为从弹配备导引头，节约了成本，但过载会在通信拓扑切换时出现跳变，而且导弹的切向过载指令是时变的，不利于应用。为了同时解决时变通信拓扑和通信延迟的问题，针对平面内的静止目标，Sun等［28］先通过反馈线性化得到每枚导弹的线性制导律。接着基于图论，将所提出的协同制导律的一致性问题转化为弹目距离和前置角误差系统的稳定性问题，并通过李雅普诺夫的方法证明了存在时变交流时间延迟的固定／时变同步网络稳定的充分条件，但这种协同制导方法只能得到线性化后系统的控制项表达式及稳定性判据，没有给出导弹的过载表达式。

4 多导弹协同制导方法

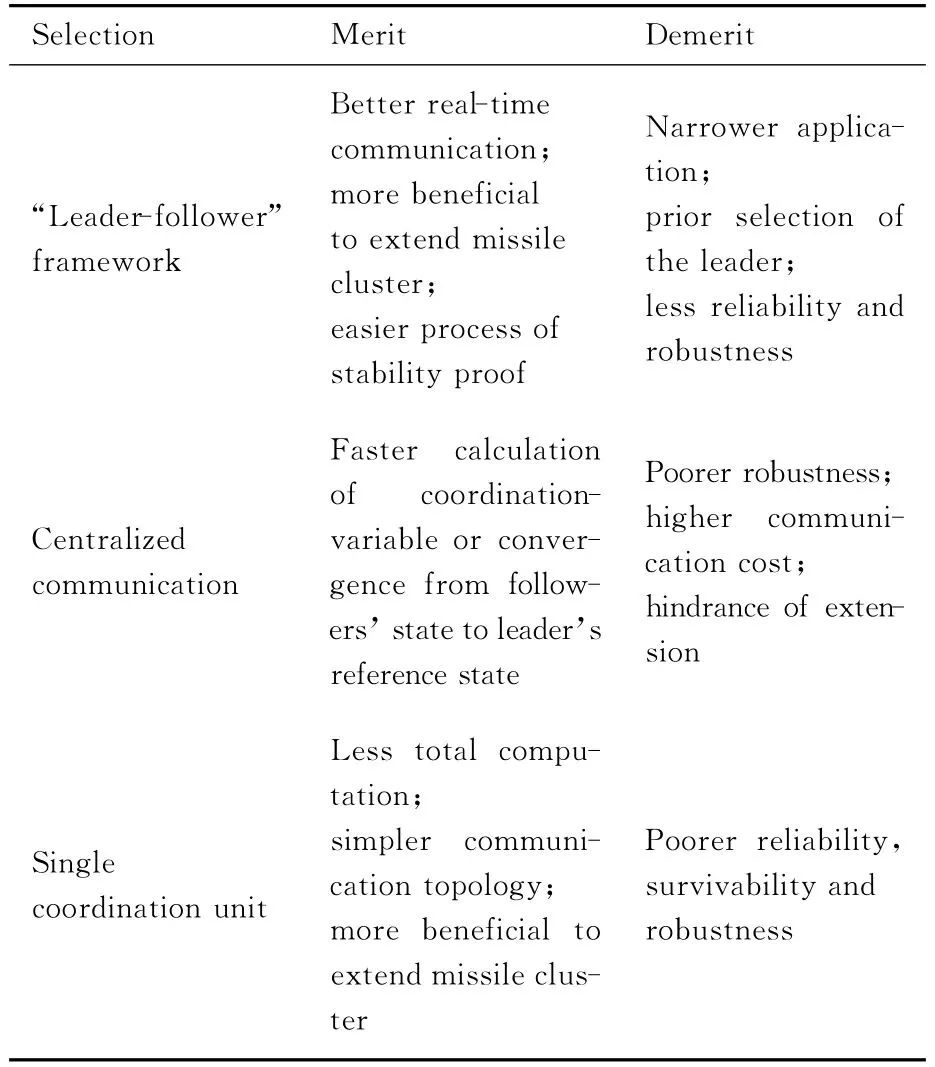
通过对多导弹协同制导方法的研究综述（文献来源见表1）可以发现，根据不同的任务类型和硬件要求所选择的协同制导架构、通信拓扑类型和协调单元的数量都会对协同制导算法的性能产生影响。表2总结了采用“领弹－从弹”协同制导架构，集中式通信拓扑和只有一个协调单元的优缺点，而采用双层协同制导架构，分布式通信拓扑和多个协调单元的优缺点则分别与之相反。

此外，现有的理论研究尽管可以解决一些技术问题，但仍然有很多有价值且具有挑战性的问题值得继续深入研究。下面给出未来有可能的几个主要研究方向。

表1 文献来源
Table 1 Sources of references

Names of database SCIE EI CSCD Others Quantities of reference 10 20 1 2

表2 “领弹－从弹”架构、集中式通信和单一协调单元的特点
Table 2 Performance of “leader－follower”framework，centralized communication and single coordination unit

Selection Merit Demerit“Leader－follower”framework Better real－time communication；more beneficial to extend missile cluster；easier process of stability proof Narrower application；prior selection of the leader；less reliability and robustness Centralized communication Faster calculation of coordinationvariable or convergence from followers’state to leader’s reference state Poorer robustness；higher communication cost；hindrance of extension Single coordination unit Less total computation；simpler communication topology；more beneficial to extend missile cluster Poorer reliability，survivability and robustness

4．1 时间协同制导方法的性能与效率

通过上文综述部分可以发现，在协同制导架构、通信拓扑类型和协调单元的数量均确定的情况下，现有协同制导律所存在的不足完全是由其所采用的协调变量／参考运动状态和制导／控制方法所导致的，例如：若采用剩余时间作为协调变量则会出现剩余时间的估计误差较大的问题；若采用弹目距离和前置角作为参考运动状态则需要时变的切向过载指令；若采用滑模控制的方法则会出现抖振等。因此，在现有研究成果的基础上，可以对基于双层协同制导架构的制导方法所采用的带有时间约束的导引律、协调一致性策略和基于“领弹－从弹”协同制导架构的制导方法所采用的参考运动状态、从弹跟踪方式进行改进，从而得到性能更优的协同制导律，例如：李东岩等［61］通过在目标函数中引入包围因子实现了多导弹的协同，从而避免了剩余时间的估计误差。此外，也可以通过设计新型的协同制导架构以达到目的，例如：邹丽等［29］就将两种协同制导架构进行了结合，提高了协同效率。显然，基于时间协同的制导方法在提高协同效率和性能方面还存在很大的改进空间。

4．2 复杂条件下的协同制导方法

迄今为止，多数已有的协同制导方法均是基于理想条件、针对低机动能力目标、忽略许多限制条件下得出的。

首先，基于理想条件设计的协同导引律在实际应用中往往会因为更加复杂的应用条件而产生较大误差，从而无法实现协同或无法发挥出协同攻击所应有的优势。因此，在未来对协同制导方法进行设计时，应该充分考虑到这些复杂环境的影响，从而进一步提高协同制导方法在非理想攻击条件下的实用价值。其次，在现有的协同制导方法中，往往将攻击目标设定为舰船，而舰船的机动能力相对于导弹而言几乎可以忽略不计。然而，对于高超声速武器，也需要采用多导弹协同拦截［5，62－63］。对于这些高超声速的目标，就必须要考虑其机动能力。第三，虽然文献［5］指出目标的加速度信息可以由导引头直接测得，但这无疑对于导引头的性能提出了很高的要求。而且，现有的涉及到机动目标的协同制导方法都假设目标的过载可以直接测得，这也就不得不考虑导弹导引头的性能限制，例如：因为导引头精度有限，探测到的目标信息会存在误差。虽然文献［61］考虑到了这个问题，将估计器与制导律进行了综合设计，但却无法直接得出导弹的过载指令，不利于应用。此外，导弹对于导引头框架角和过载的限制在未来进行协同制导律设计时也应该加以考虑。第四，导弹集群在保证时间协同的基础上，还可以考虑协同避障的问题［64－65］。最后，导弹在进行制导律设计时往往忽略动力学信息，如果只考虑制导回路而忽视控制回路则无法保证系统的稳定性。对于一些有特殊动力学特征的导弹，如：旋转导弹和高超声速导弹等，在设计其协同制导律时，还应该考虑其动力学特性，即要实现制导与控制的综合设计。

上述研究工作的不足也为深化复杂条件下的协同制导方法研究提供了广阔的研究空间和更有实用价值的研究课题。

4．3 其他协同策略

在协同目标或协同策略方面，现有的大多数协同制导方法都是关于时间协同的研究成果，但多导弹的协同攻击策略绝不仅仅局限于时间的协同，还可以在弹道角、空间位置和导弹功能等方面实现协同攻击以提高攻击效率。

对于装甲类目标，为了增强毁伤效果，导弹的攻击往往需要满足特定落角，而带落角约束的导引律也一直是一个研究的热门。此外，两组导弹集群的弹道角若能保持90°的差距，则它们均可以攻击目标的头部或侧面，而目标将很难选择一种合适的机动方式以摆脱攻击［43］。Shaferman和Shima［66］基于最优控制，针对平面内的机动目标，设计了一种可以约束导弹间相对弹道角的协同制导律，但由于采用了综合代价函数设计，使其在应用时会受到较多的约束［53］。然而，具有相对弹道角约束的协同制导问题却可以作为今后研究的一个重要方向。同样，为了增强打击效果和突防能力，导弹在阵型上的协同问题也是未来的研究方向，例如：可以设计导弹集群的阵型，使其具有减小雷达波反射面积，并对拦截器进行干扰，或对导弹进行战术伪装等，并通过设计协同制导律来实现阵型的保持。由于在突防过程中难免会有导弹被击落，所以这种为了保持阵型的协同制导问题可以作为一种时变问题进行处理。在本文引言部分曾提到的“侦查－打击－评估”一体化协同作战模式也可以作为一种协同打击的特殊形式而进行制导律设计。这种协同作战模式显然需要针对导弹的不同功能至少设计3种协同制导律，而其设计难度也要远远高于现有的协同制导律。此外，针对“领弹－从弹”协同制导架构，也可以设计一种当从弹遇到拦截器时主动牺牲以保障领弹安全的协同制导律。

5 结束语

随着人们对于多导弹协同打击的关注程度越来越高，对于这项技术的功能性和应用性也将提出更高的要求，这也将促进对于多导弹协同制导方法的研究更加蓬勃发展。虽然各国科研人员已经在这个领域中开展了一些研究工作，也取得了一些突破性的研究成果，但仍有许多理论与工程问题尚未解决。随着导弹制导技术与协同理论的进一步发展，将为解决多导弹协同制导问题提供更多有效的途径，也必将为工程应用奠定更加坚实的基础。

参考文献

［1］王芳，涂震飚，魏佳宁．战术导弹协同突防关键技术研究［J］．战术导弹技术，2013（3）：13－17．

WANG F，TU Z B，WEI J N．Research on key technical problems of cooperative penetration for tactical missile［J］．Tactical Missile Technology，2013（3）：13－17 （in Chinese）．

［2］王建青，李帆，赵建辉，等．多导弹协同制导律综述［J］．飞行力学，2011，29（4）：6－10．

WANG J Q，LI F，ZHAO J H，et al．Summary of guidance law based on cooperative attack of multi－missile method［J］．Flight Dynamics，2011，29（4）：6－10（in Chinese）．

［3］肖志斌，何冉，赵超．导弹编队协同作战的概念及其关键技术［J］．航天电子对抗，2013，29（1）：1－3．

XIAO Z B，HE R，ZHAO C．Cooperative combat of missile formation：Concepts and key technologies［J］．Aerospace Electronic Warfare，2013，29（1）：1－3（in Chinese）．

［4］张克，刘永才，关世义．体系作战条件下飞航导弹突防与协同攻击问题研究［J］．战术导弹技术，2005（2）：1－7．

ZHANG K，LIU Y C，GUAN S Y．An investigation into the issues of penetration and cooperative engagement for aerodynamic missile under the condition of systems coutermeasures［J］．Tactical Missile Technology，2005（2）：1－7（in Chinese）．

［5］赵启伦，陈建，董希旺，等．拦截高超声速目标的异类导弹协同制导律研究［J］．航空学报，2016，37（3）：936－948．

ZHAO Q L，CHEN J，DONG X W，et al．Cooperative guidance law for heterogeneous missiles intercepting hypersonic weapon［J］．Acta Aeronautica et Astronautica Sinica，2016，37（3）：936－948（in Chinese）．

［6］胡正东，林涛，张士峰，等．导弹集群协同作战系统概念研究［J］．飞航导弹，2007（10）：13－18．HU Z D，LIN T，ZHANG S F，et al．The concept study of multi－missile cooperative combat system［J］．Aerodynamic Missile Journal，2007（10）：13－18（in Chinese）．

［7］赵世钰，周锐．基于协调变量的多导弹协同制导［J］．航空学报，2008，29（6）：1605－1611．ZHAO S Y，ZHOU R．Multi－missile cooperative guidance using coordination variables［J］．Acta Aeronautica et Astronautica Sinica，2008，29（6）：1605－1611（in Chinese）．

［8］林涛，刘永才，关成启，等．飞航导弹协同作战使用方法探讨［J］．战术导弹技术，2005（2）：8－12．

LIN T，LIU Y C，GUAN C Q，et al．An investigation into the methods of cooperative engagement for aerodynamic missile［J］．Tactical Missile Technology，2005（2）：8－12（in Chinese）．

［9］ JEON I S，LEE J I，TAHK M J．Impact－time－control guidance law for anti－ship missiles［J］．IEEE Transactions on Control Systems Technology，2006，14（2）：260－266．

［10］张友安，马国兴，王兴平．多导弹时间协同制导：一种领弹－被领弹策略［J］．航空学报，2009，30（6）：1109－1118．

ZHANG Y A，MA G X，WANG X P．Time－cooperative guidance for multi－missiles：A leader－follower strategy［J］．Acta Aeronautica et Astronautica Sinica，2009，30（6）：1109－1118（in Chinese）．

［11］肖增博，雷虎民，滕江川，等．多导弹协同制导规律研究现状及展望［J］．航空兵器，2011（6）：18－22．

XIAO Z B，LEI H M，TENG J C，et al．The present status and prospect of multi－missile cooperative guidance law［J］．Aero Weaponry，2011（6）：18－22（in Chinese）．

［12］张友安，王星亮，吴华丽，等．带攻击时间约束的导引律综述［J］．海军航空工程学院学报，2015，30（4）：301－309．

ZHANG Y A，WANG X L，WU H L，et al．Survey of guidance law with attack time constraint［J］．Journal of Naval Aeronautical and Astronautical University，2015，30（4）：301－309（in Chinese）．

［13］ ZHAO S Y，ZHOU R，WEI C，et al．Design of time－constrained guidance laws via virtual leader approach［J］．Chinese Journal of Aeronautics，2010，23（1）：103－108．

［14］王晓芳，林海．多约束条件下导弹协同作战制导律［J］．弹道学报，2012，24（3）：59－64．

WANG X F，LIN H．A guidance law for multiple missiles combating cooperatively under multiple constraints［J］．Journal of Ballistics，2012，24（3）：59－64（in Chinese）．

［15］ HARL N，BALAKRISHNAN S N．Impact time and angle guidance with sliding mode control［J］．IEEE Transactions on Control Systems Technology，2012，20（6）：1436－1449．

［16］ KUMAR S R，GHOSE D．Sliding mode control based guidance law with impact time constraints［C］／Proceedings of the American Control Conference．Piscataway，NJ：IEEE Press，2013：5760－5765．

［17］ GUO C，LIANG X G．Cooperative guidance law for multiple near space interceptors with impact time control［J］．International Journal of Aeronautical ＆ Space Sciences，2014，15（3）：281－292．

［18］ ZHAO S Y，ZHOU R，WEI C．Design and feasibility analysis of a closed－form guidance law with both impact angle and time constraints［J］．Journal of Astronautics，2009，30（3）：1064－1072．

［19］ KANG S，KIM H J．Differential game missile guidance with impact angle and time constraints［J］．World Congress，2011，18（1）：3920－3925．

［20］ WANG X，ZHENG Y，LIN H．Integrated guidance and control law for cooperative attack of multiple missiles［J］．Aerospace Science and Technology，2015，42：1－11．

［21］施建洪，张友安，梁勇．飞行器落角与撞击时间控制研究［J］．海军航空工程学院学报，2011，26（4）：398－404．

SHI J H，ZHANG Y A，LIANG Y．Research on Impact angle control and impact time control for aircraft［J］．Journal of Naval Aeronautical and Astronautical University，2011，26（4）：398－404（in Chinese）．

［22］ ZHAO E，WANG S，CHAO T，et al．Multiple missiles cooperative guidance based on leader－follower strategy［C］／Proceedings of 2014IEEE Chinese Guidance，Navigation and Control Conference．Piscataway，NJ：IEEE Press，2014：1163－1167．

［23］ MCLAIN T W，BEARD R W．Coordination variables，coordination functions，and cooperative timing missions［J］．Journal of Guidance，Control，and Dynamics，2005，28（1）：150－161．

［24］ KUMAR S R，GHOSE D．Cooperative rendezvous guidance using sliding mode control for interception of stationary targets［C］／Proceedings of Third International Conference on Advances in Control and Optimization of Dynamical Systems．Dusseldorf：IFAC Secretariat，2014：477－483．

［25］邹丽，丁全心，周锐．异构多导弹网络化分布式协同制导方法［J］．北京航空航天大学学报，2010，36（12）：1432－1435．

ZOU L，DING Q X，ZHOU R．Distributed cooperative guidance for multiple heterogeneous networked missiles［J］．Journal of Beijing University of Aeronautics and Astronautics，2010，36（12）：1432－1435（in Chinese）．

［26］王晓芳，洪鑫，林海．一种控制多弹协同攻击时间和攻击角度的方法［J］．弹道学报，2012，24（2）：1－5．

WANG X F，HONG X，LIN H．A method of controlling impact time and impact angle of multiple－missiles cooperative combat［J］．Journal of Ballistics，2012，24（2）：1－5（in Chinese）．

［27］马国欣，张友根，张友安．一领弹控制下的多导弹时间协同三维制导律［J］．海军航空工程学院学报，2013，28（1）：11－16．

MA G X，ZHANG Y G，ZHANG Y A．Leader－controlled three－dimensional guidance law for time－cooperative multimissiles［J］．Journal of Naval Aeronautical and Astronautical University，2013，28（1）：11－16（in Chinese）．

［28］ SUN X，ZHOU R，HOU D，et al．Consensus of leaderfollowers system of multi－missile with time－delays and switching topologies［J］．Optik－International Journal for Light and Electron Optics，2014，125（3）：1202－1208．

［29］邹丽，孔繁峨，周锐，等．多导弹分布式自适应协同制导方法［J］．北京航空航天大学学报，2012，38（1）：128－132．

ZOU L，KONG F E，ZHOU R，et al．Distributed adaptive cooperative guidance for multi－missile salvo attack［J］．Journal of Beijing University of Aeronautics and Astronautics，2012，38（1）：128－132（in Chinese）．

［30］邹丽，周锐，赵世钰，等．多导弹编队齐射攻击分散化协同制导方法［J］．航空学报，2011，32（2）：281－290．

ZOU L，ZHOU R，ZHAO S Y，et al．Decentralized cooperative guidance for multiple missile groups in salvo attack［J］．Acta Aeronautica et Astronautica Sinica，2011，32（2）：281－290（in Chinese）．

［31］ ZHAO E，TAO C，WANG S，et al．An adaptive parameter cooperative guidance law for multiple flight vehicles［C］／Proceedings of AIAA Atmospheric Flight Mechanics Conference．Reston：AIAA，2015：2709－2718．

［32］孙雪娇，周锐，吴江，等．多导弹分布式协同制导与控制方法［J］．北京航空航天大学学报，2014，40（1）：120－124．

SUN X J，ZHOU R，WU J，et al．Distributed cooperative guidance and control for multiple missiles［J］．Journal of Beijing University of Aeronautics and Astronautics，2014，40（1）：120－124（in Chinese）．

［33］周锐，孙雪娇，吴江，等．多导弹分布式协同制导与反步滑模控制方法［J］．控制与决策，2014，29（9）：1617－1622．

ZHOU R，SUN X J，WU J，et al．Multi－missile distributed cooperative guidance integrating backstepping sliding mode control［J］．Control and Decision，2014，29（9）：1617－1622（in Chinese）．

［34］后德龙，陈彬，王青，等．碰撞自规避多弹分布式协同制导与控制［J］．控制理论与应用，2014，31（9）：1133－1142．

HOU D L，CHEN B，WANG Q，et al．Collision avoidance multi－missile distributed cooperative guidance and control［J］．Control Theory and Applications，2014，31（9）：1133－1142（in Chinese）．

［35］彭琛，刘星，吴森堂，等．多弹分布式协同末制导时间一致性研究［J］．控制与决策，2010，25（10）：1557－1561．

PENG C，LIU X，WU S T，et al．Consensus problems in distributed cooperative terminal guidance time of multimissiles［J］．Control and Decision，2010，25（10）：1557－1561（in Chinese）．

［36］ ZHAO J，ZHOU R．Unified approach to cooperative guidance laws against stationary and maneuvering targets［J］．Nonlinear Dynamics，2015，81（4）：1635－1647．

［37］ ZHAO J，ZHOU R，DONG Z．Three－dimensional cooperative guidance laws against stationary and maneuvering targets［J］．Chinese Journal of Aeronautics，2015，28（4）：1104－1120．

［38］张保峰，宋俊红，宋申民．具有角度约束的多导弹协同制导研究［J］．弹箭与制导学报，2014，34（1）：13－15．

ZHANG B F，SONG J H，SONG S M．Research on multi－missile cooperative guidance with angle constraint［J］．Journal of Projectiles Rockets Missiles and Guidance，2014，34（1）：13－15（in Chinese）．

［39］王青，后德龙，李君，等．具有角度约束的多导弹协同制导研究［J］．兵工学报，2014，35（7）：982－989．

WANG Q，HOU D L，LI J，et al．Consensus analysis of multi－missile decentralized cooperative guidance time with time－delays and topologies uncertainty［J］．Acta Armamentarii，2014，35（7）：982－989（in Chinese）．

［40］ HA I J，HUR J S，KO M S，et al．Performance analysis of PNG laws for randomly maneuvering targets［J］．IEEE Transactions on Aerospace and Electronic Systems，1990，26（5）：713－721．

［41］ JEON I S，LEE J I，TAHK M J．Homing guidance law for cooperative attack of multiple missiles［J］．Journal of Guidance，Control，and Dynamics，2010，33（1）：275－280．

［42］ SONG S H，HA I J．A Lyapunov－like approach to performance analysis of 3－dimensional pure PNG laws［J］．IEEE Transactions on Aerospace and Electronic Systems，1994，30（1）：238－248．

［43］ WU X，WU S，XING Z．A guidance law with impact angle constraint for anti－ship missiles cooperative attack［C］／Proceedings of the 33rd Chinese Control Conference．Piscataway，NJ：IEEE Press，2014：954－959．

［44］ ZENG J，DOU L，XIN B．Cooperative salvo attack using guidance law of multiple missiles［J］．Journal of Advanced Computational Intelligence and Intelligent Informatics，2015，19（2）：301－306．

［45］ SUN X，XIA Y Q．Optimal guidance law for cooperative attack of multiple missiles based on optimal control theory［J］．International Journal of Control，2012，85（8）：1063－1070．

［46］ MORGAN R W，THARP H，VINCENT T L．Minimum energy guidance for aerodynamically controlled missiles［J］．IEEE Transactions on Automatic Control，2011，56（9）：2026－2037．

［47］张友安，胡云安．导弹控制和制导的非线性设计方法［M］．北京：国防工业出版社，2003：160－163．

ZHANG Y A，HU Y A．Nonlinear design approaches for missile control and guidance［M］．Beijing：National Defense Industry Publisher，2003：160－163（in Chinese）．

［48］ WANG X，ZHANG Y，WU H．Distributed cooperative guidance of multiple anti－ship missiles with arbitrary impact angle constraint［J］．Aerospace Science and Technology，2015，46：299－311．

［49］马国欣，张友安．多导弹时间协同分布式导引律设计［J］．控制与决策，2014，29（5）：843－847．

MA G X，ZHANG Y A．Time－cooperative distributed guidance law design for multi－missiles［J］．Control and Decision，2014，29（5）：843－847（in Chinese）．

［50］ ZHAO S Y，ZHOU R．Cooperative guidance for multimissile salvo attack［J］．Chinese Journal of Aeronautics，2008，21（6）：533－539．

［51］ HOU J，JI X，LIU Z，et al．Distributed multi－missile salvo attack［C］／Proceedings of the 33rd Chinese Control Conference．Piscataway，NJ：IEEE Press，2014：887－890．

［52］ PARK J，YOO J H，KIM H J．Two distributed guidance approaches for rendezvous of multiple agents［C］／Proceedings of the 2010International Conference on Control，Automation and Systems．Piscataway，NJ：IEEE Press，2010：2128－2132．

［53］ SONG L，ZHANG Y，HUANG D，et al．Cooperative simultaneous attack of multi－missiles under unreliable and noisy communication network：A consensus scheme of impact time［J］．Aerospace Science and Technology，2015，47：31－41．

［54］孙雪娇，周锐，吴江，等．攻击机动目标的多导弹分布式协同制导律［J］．北京航空航天大学学报，2013，39（10）：1403－1407．

SUN X J，ZHOU R，WU J，et al．Distributed cooperative guidance law for multiple missiles attacking maneuver target［J］．Journal of Beijing University of Aeronautics and Astronautics，2013，39（10）：1403－1407（in Chinese）．

［55］ HOU D，WANG Q，SUN X，et al．Finite－time cooperative guidance laws for multiple missiles with acceleration saturation constraints［J］．IET Control Theory ＆ Applications，2015，9（10）：1525－1535．

［56］ WEI X，WANG Y，DONG S，et al．A three－dimensional cooperative guidance law of multimissile system［J］．International Journal of Aerospace Engineering，2015，2015（4）：1－8．

［57］ DAUGHTERY E，QU Z．Optimal design of cooperative guidance law for simultaneous strike［C］／Proceedings of the 53rd IEEE Conference on Decision and Control．Piscataway，NJ：IEEE Press，2014：988－993．

［58］ ZHANG Y A，MA G X，WU H L．A biased proportional navigation guidance law with large impact angle constraint and the time－to－go estimation［J］．Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2014，228（10）：1725－1734．

［59］ LEE J I，JEO I S，TAHK M J．Guidance law to control impact time and angle［J］．IEEE Transactions on Aerospace and Electronic Systems，2007，43（1）：301－310．

［60］ QU Z，WANG J，HULL R A．Cooperative control of dynamical systems with application to autonomous vehicles［J］．IEEE Transactions on Automatic Control，2008，53（4）：894－911．

［61］李东岩，张志峰，王飞，等．基于制导／估计综合设计的协同制导律［J］．北京理工大学学报，2012，32（5）：508－512．

LI D Y，ZHANG Z F，WANG F，et al．Cooperative guidance law based on integration design of guidance and estimation［J］．Transactions of Beijing Institute of Technology，2012，32（5）：508－512（in Chinese）．

［62］ GHOSH S，GHOSE D，RAHA S．Three dimensional Retro－PN based impact time control for higher speed nonmaneuvering targets［C］／Proceedings of the 52nd IEEE Conference on Decision and Control．Piscataway，NJ：IEEE Press，2013：4865－4870．

［63］ GHOSH S，GHOSE D，RAHA S．Retro－PN based simultaneous salvo attack against higher speed nonmaneuvering targets［C］／Proceedings of the third International Conference on Advances in Control and Optimization of Dynamical Systems．Dusseldorf：IFAC，2014：34－40．

［64］ ZHAO J，ZHOU S Y，ZHOU R．Distributed time－constrained guidance using nonlinear model predictive control［J］．Nonlinear Dynamics，2016，84（3）：1399－1416．

［65］ ZHAO J，ZHOU R．Obstacle avoidance for multi－missile network via distributed coordination algorithm［J］．Chinese Journal of Aeronautics，2016，29（2）：441－447．

［66］ SHAFERMAN V，SHIMA T．Cooperative optimal guidance laws for imposing a relative intercept angle［J］．Journal of Guidance，Control，and Dynamics，2015，38（8）：1395－1408．

Review of multi－missile cooperative guidance

ZHAO Jianbo，YANG Shuxing＊

School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

Abstract：This paper reviews the development history of multi－missile cooperative guidance，including the main research findings and the latest progresses．In view of the fact that the existing results of the research on cooperative guidance are mainly concerned with time coordination and the open－loop cooperative guidance has been well reviewed，this paper focuses on the close－loop time cooperative guidance accordingly．Based on its framework，the multi－missile time cooperative guidance can be categorized into two types：the two－level guidance，and“leader－follower”one．It can be also categorized into centralized and decentralized one based on communication topology among missiles．The two types of cooperative guidance frameworks are discussed first．The centralized and decentralized multi－missile cooperative guidance laws are then analyzed．The merits and demerits of these types of cooperative guidance laws are also summarized．A short discussion section is included to propose several promising research directions for further investigation．

Keywords：multi－missile；missile guidance；cooperative guidance；communication；two－level coordination；leader－follower；salvo attack；impact time

Received：2016－03－24；Revised：2016－04－11；Accepted：2016－04－29；Published online：2016－05－04 09：37

URL：www．cnki．net／kcms／detail／11．1929．V．20160504．0937．002．html

Foundation item：National Natural Science Foundation of China（11532002）

中图分类号：V249．1；TJ765．3

文献标识码：A

文章编号：1000－6893（2017）01－020256－13

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

DOI：10．7527／S1000－6893．2016．0136

收稿日期：2016－03－24；退修日期：2016－04－11；录用日期：2016－04－29；网络出版时间：2016－05－04 09：37

网络出版地址：www．cnki．net／kcms／detail／11．1929．V．20160504．0937．002．html

基金项目：国家自然科学基金（11532002）

＊通讯作者．E－mail：yangshx＠bit．edu．cn

引用格式：赵建博，杨树兴．多导弹协同制导研究综述［J］．航空学报，2017，38（1）：020256．ZHAO J B，YANG S X．Review of multimissile cooperative guidance［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：020256．