学界 | 带引导的进化策略：摆脱随机搜索中维数爆炸的魔咒

会员服务 ·

学界 | 带引导的进化策略：摆脱随机搜索中维数爆炸的魔咒

2018 年 7 月 22 日 机器之心

选自arXiv

作者：Niru Maheswaranathan、Luke Metz、

George Tucker、Jascha Sohl-Dickstein

机器之心编译

参与：Geek AI、淑婷

机器学习模型优化的很多案例中都需要对真实梯度未知的函数进行优化。虽然真实梯度未知，但其代理梯度信息却可用。本文提出了一种带引导的进化策略——一种利用代理梯度方向和随机搜索的优化方法，并将该方法应用于合成梯度等问题，最终证明该方法在标准进化策略和直接遵循代理梯度的一阶方法上得到提升。

1 引言

机器学习模型的优化常常涉及最小化代价函数，其中代价关于模型参数的梯度是已知的。当梯度信息可用时，梯度下降和变量等一阶方法因其易于实现、存储效率高（通常需要与参数维度相匹配的存储空间）和收敛有保障 [1] 而广受欢迎。然而，当梯度信息不可用时，我们转向零阶优化方法，包括随机搜索方法，例如最近重新流行起来的进化策略 [2，3，4]。

然而，如果只有部分梯度信息可用，我们又该怎么做呢？也就是说，如果我们能够获得与真实梯度相关的代理梯度，但是这种替代方法会以某种未知的方式产生偏置，我们该怎么做？事实上，各种各样的机器学习问题中都会出现这种情况。例如，Wu 等人在论文 [5] 中说明，在展开优化（通过一种展开优化过程计算梯度）问题中，与在许多展开步骤之后计算（代价高昂的）梯度相比，计算小规模展开步骤的梯度是存在偏置的。在其它应用中，真实梯度并不提供学习信号，我们可以用代理梯度作为一种替代。例如，在神经网络的量化问题中，我们希望用离散（甚至二值化的）权重和/或激活函数来训练神经网络。实现这个目标的一种方法是使用直流评估器 [6]（STE），它通过平滑处理（或直接忽略）神经网络中一些执行量化的节点来生成代理梯度，并且使用该梯度来训练网络。然而，我们并不能保证这个方向是一个好的梯度下降方向。最后，代理梯度也出现在强化学习算法中，例如，actor-critic 方法 [7]，和 Q-learning [8，9，10]。

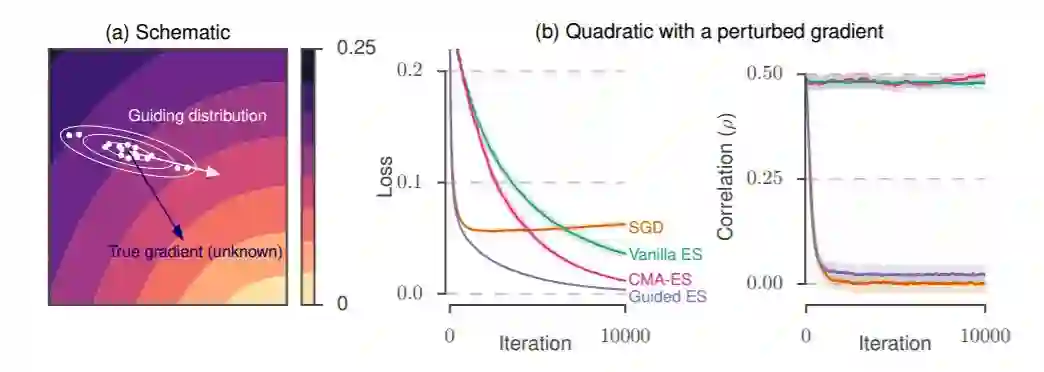
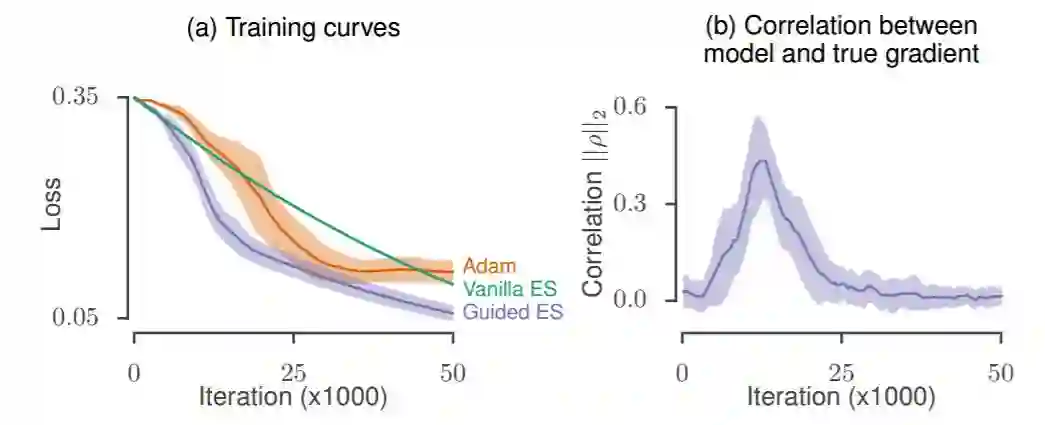
图 1:（a）带引导的进化策略示意图。我们使用沿着给定子空间（白色箭头）延伸的分布（白色等高线）进行随机搜索，而不是使用真正的梯度方向（蓝色箭头）。（b）对不同算法的二次损失进行比较，向梯度显式地加入一个偏置，用来模拟真实梯度未知的情况。优化过程中显示了损失（左图）以及代理梯度和真实梯度（右图）之间的相关性。实验细节请参阅 4.1 节。

直观地说，有两种极端的方法可以使用代理梯度进行优化。一方面，你可以完全忽略代理梯度信息并执行零阶优化，使用进化策略等方法来估计梯度下降的方向。当参数的维度较大时，这些方法的收敛性较差 [11]。另一方面，你可以直接将代理梯度输入到一阶优化算法中去。然而，代理梯度中存在的偏置会影响到目标问题的优化 [12]。理想情况下，我们希望有一种方法能够融合上述两种方法互补的优势：我们希望将通过进化策略估计出的无偏梯度下降方向与通过代理梯度得到的低方差估计结合起来。在本文中，我们提出了一种被称为「带引导的进化策略」（Guided ES）的方法。

我们的想法是跟踪一个低维子空间，这个子空间是由优化过程中代理梯度的最近历史定义的（受拟牛顿法启发），我们称之为引导子空间。然后，我们优先在这个子空间内执行有限差分随机搜索（就像在进化策略中那样）。通过将搜索样本集中在真实梯度具有非负支持的低维子空间中，我们可以显著减小搜索方向的方差。本文的贡献如下：

将代理梯度信息与随机搜索相结合的新方法。
基于技术的偏置-方差权衡分析。（见 3.3 节）
为相关方法选择最优超参数的方案。（见 3.4 节）
示例问题的应用。（见第 4 节）

文中方法的演示程序，请参阅：https://github.com/brain-research/guided-evolutionary-strategies

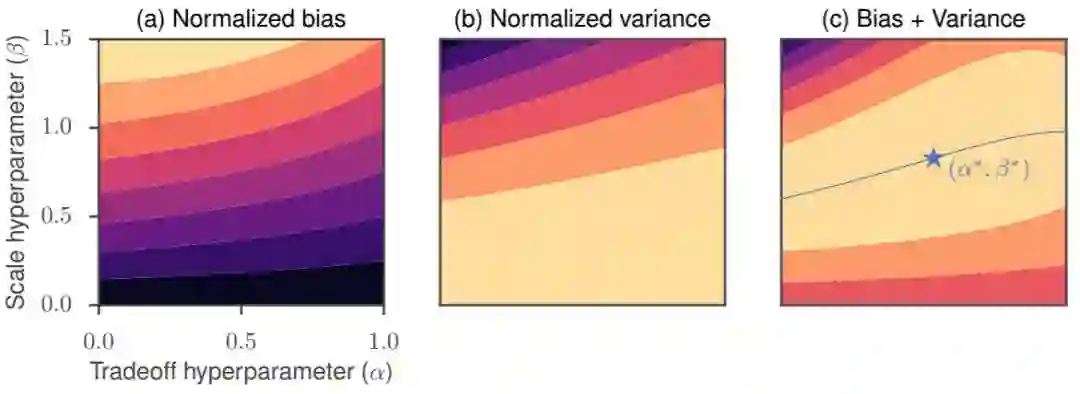
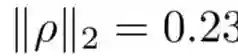
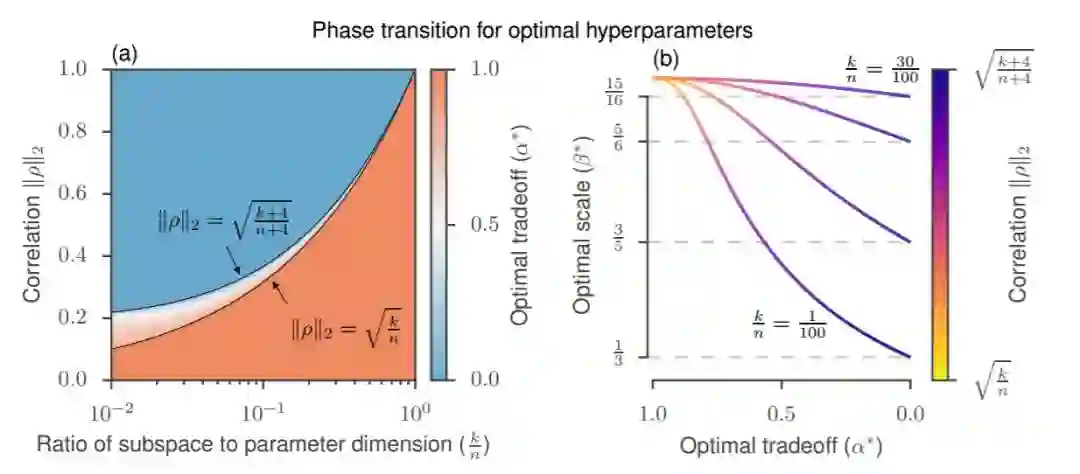
图 2：在带引导的进化策略中对偏置-方差权衡进行探索。归一化偏置˜b 的等高线图（a），归一化方差 v˜的等高线图（b），以及前面二者之和的等高线图（c）。它们是关于权衡（α）和规模（β）超参数的函数，其中，是固定的。在这些等高线图中，子空间维数被设定为 k=3，参数维数被设定为 n=100。（c）中蓝色的线表示对于每一个 α 值来说最优的 β，星标表示全局最优点。

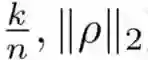
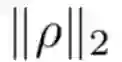
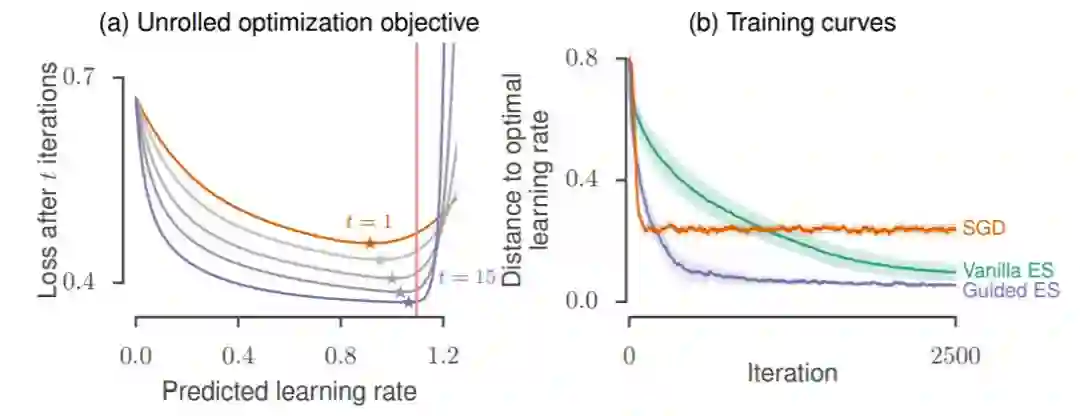
图 3：选择最优超参数。（a）阴影区域显示了在平面中最优超参数的不同机制。细节请参阅 3.4 节。（b）随着增加，最优超参数从 α^ ∗ = 1, β^∗ = n /(n+2) 到α^∗ = 0, β^∗ = k /(k+2) 划出了一条曲线。

图 4：展开优化。（a）少量展开优化步骤（t）展开优化过程中的损失情况的偏置。（b）用于训练多层感知器的训练曲线（显示为与最优点的距离），它作为一个用于优化的函数的特征值的函数去预测最佳学习率。细节请参阅 4.2 节。

图 5：作为带引导的进化策略的引导子空间的合成梯度。（a）使用合成梯度最小化目标二次问题时的损失曲线。（b）带引导的进化策略的优化过程中合成更新方向和真实梯度的相关性。

论文：Guided evolutionary strategies: escaping the curse of dimensionality in random search

论文链接：https://arxiv.org/pdf/1806.10230.pdf

摘要：机器学习中很多应用都需要对一个真实梯度未知的函数进行优化，但是其代理梯度信息（可能与真实梯度相关但不一定完全相同的方向）是可知的。当一个近似梯度比完整的梯度更容易计算时（例如，在元学习或展开优化中），或者当一个真实梯度比较棘手且可以被代理梯度替换时（例如，在某些强化学习应用中，或使用合成梯度时），就会出现这种情况。我们提出了带引导的进化策略，这是一种利用代理梯度方向和随机搜索的优化方法。我们为进化策略定义了一个搜索分布，它沿着代理梯度指向的引导子空间延伸。这使我们能够估计出梯度下降方向，并且接着将这个方向传递给一阶优化器。我们定性和定量地刻画了因为调整搜索分布在引导子空间上的伸展程度而产生的权衡，并由此推导出了一个超参数的集合，该集合可以很好地解决各类问题。最终，我们将该方法应用于包括截断展开优化和合成梯度问题在内的示例问题，证明了该方法在标准进化策略和直接遵循代理梯度的一阶方法上的提升。我们为带引导的进化策略（Guided ES）提供了一个演示程序，链接如下：http://github.com/brain-research/guided-evolutionary-strategies。