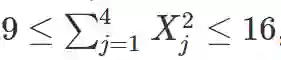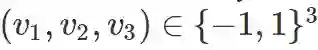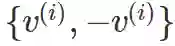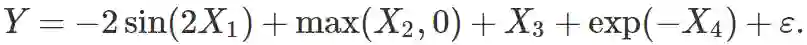前沿 | UC Berkeley提出特征选择新方法：条件协方差最小化

选自BAIR Blog

作者：Jianbo Chen、Mitchell Stern

机器之心编译

参与：Nurhachu Null、路雪

UC Berkeley 近日提出了一种新型特征选择方法 CCM，该方法基于最小化条件协方差算子的迹来进行特征选择。研究者的实验证明该方法在多个合成和现实数据集上达到了不输当前先进方法的性能。相关论文《Kernel Feature Selection via Conditional Covariance Minimization》被 NIPS 2017 接收。

• 论文链接：https://papers.nips.cc/paper/7270-kernel-feature-selection-via-conditional-covariance-minimization.pdf

• GitHub 链接：https://github.com/Jianbo-Lab/CCM

降维可以增强模型的可解释性，特征选择则是常用的降维方法。随着大型数据集变得流行，近年来包括文本分类、微阵列数据中的基因选择、人脸识别等现实任务见证了特征选择的广泛使用。BAIR 研究了监督性特征选择的问题，监督特征选择需要寻找一个输入特征的子集来较好地解释输出结果。这个方法可以通过消除冗余或者噪声特征来降低下游学习（downstream learning）的计算成本，同时还能通过保留下来的特征来提供对数据的洞见。

特征选择算法通常可分为三个主要的类别：滤波器（filter）方法、封装（wrapper）方法以及嵌入（embedded）方法。滤波器方法基于数据的本质属性选择特征，与所用的学习算法无关。例如，我们可以计算每个特征和响应变量之间的相关性，然后选择相关性最高的变量。相比之下，封装方法就更加具体，它的目标是寻找能够使某个预测器的性能最优化的特征。例如，我们可以训练多个支持向量机，每个支持向量机使用不同的特征子集，然后选择在训练数据上损失最小的特征子集。因为特征子集的数量是指数规模的，所以封装方法通常会使用贪心算法。最后，嵌入方法是将特征选择和预测结合成一个问题的多目标技术，它通常会优化一个目标函数，这个目标函数结合了拟合优度和对参数数量的惩罚。一个例子就是构建线性模型的 LASSO 方法，它用ℓ1 penalty 来表征对参数数目的惩罚。

本文提出了条件协方差最小化（CCM）方法，这是一个统一前两个观点的特征选择方法。在以下部分中，BAIR 研究者首先描述了自己的方法。然后我们通过几个综合实验证明该方法能够捕获特征集之间的联合非线性关系。最后，一系列现实任务证明，该算法具有和其他几种特征选择算法相当或者优于它们的性能。

特征选择的公示表达

理解特征选择问题的一种方式是从依赖的角度来看。理想情况下，我们希望先确定一个大小为 m 的特征子集 T，这样剩下的特征独立于 T 的响应。然而，如果 m 太小，则这可能无法实现。所以我们使用某个指标来量化对剩余特征条件依赖的程度，并且在所有合适大小的特征子集 T 上优化该指标。

或者，我们希望找到一个特征子集 T，它能够在特定的学习问题上最有效地预测输出 Y。在我们的框架中，将样本标签和最佳分类器所做的预测之间的均方差定义为预测误差。

方法

我们提出了一个可以在回归中同时描述依赖性和预测误差的标准。首先，我们分别介绍了在特征子集 X_T 的域和响应变量 Y 的域上的两个函数空间。每个函数空间都是一个完全的内积空间（希尔伯特空间），这个函数空间有可以将整个空间进行延展的核函数，且具备「再生性」。这样的函数空间被称作「再生核希尔伯特空间」（Reproducing Kernel Hilbert Space，RKHS）。然后，我们将响应变量的域上的 RKHS 算子定义为：在给定所选特征的情况下，描述输入数据上的响应变量的条件依赖。这个算子叫做「条件协方差算子」（conditional covariance operator）。我们用对应的经验分布计算得到的条件协方差算子的迹作为我们的优化标准，这也是最佳预测器在给定的输入数据域上的 RKHS 中的估计回归误差。在特征子集上直接最小化这个标准是很难计算的。相反，我们使用一个介于 0 和 1 之间的实值标量来对每个特征进行加权，通过这个方式将其表达为一个松弛问题。该松弛问题的目标可以用核矩阵来表示，而且可以很容易地使用基于梯度的方法进行优化。

结果

我们分别在合成数据集和现实数据集上测评了我们的方法。我们比较了现有的几个强大算法，包括递归式特征消除（RFE）、最小冗余最大关联（mRMR）、BAHSIC，以及使用互信息（MI）和皮尔逊相关系数（PC）的滤波器方法。RFE 是一个很流行的封装方法，它基于从分类器收到的得分贪婪地选择特征。mRMR 选择的特征能够捕获彼此不同的信息，但是每一个都与响应变量有很大的相关性。BAHSIC 是一个核方法，它贪婪地优化所选特征和响应变量之间的依赖。最后，滤波器方法使用互信息（MI）或者皮尔逊相关系数（PC）分别贪婪地优化所选特征子集和响应之间的相应指标。

合成数据

我们使用以下的合成数据集：

• 二元分类（Friedman et al.）。当 Y=−1 时，10 个特征 (X_1,…,X_10) 是相互独立的标准随机变量。当 Y=1 的时候，前 4 个特征是标准正态随机变量，它们满足以下条件：

剩下的 6 个特征 (X_5,…,X_10) 也是独立的标准正态随机变量。

• 三维异或作为四分类。三维超立方体有 8 个顶点，

通过元组 (v1v3,v2v3) 对它们进行分组，就得到了 4 组与各自的反面组成的成对向量

对类别 i 而言，样本可以通过等概率选择 v^(i) 或者−v^(i) 和添加噪声来生成。每个样本就额外增加 7 个标准正态噪声特征，得到的特征集总共有 10 个特征。

• 可加非线性回归。考虑以下可加模型：

每个样本额外有 6 个噪声特征，总共 10 个特征。所有的特征和噪声 ε 都是从标准正态分布中生成的。

左：二元分类数据；右：二维异或

第一个数据集表示一个标准的非线性二分类任务。第二个数据集表示一个多类别分类任务，其中每个特征都是和 Y 独立的，但是三个特征联合起来会对 Y 产生影响。第三个数据集针对可加非线性回归模型。

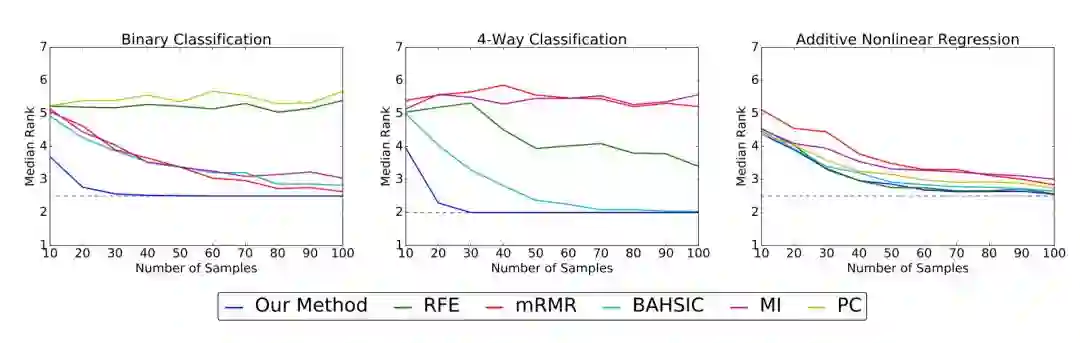
每个数据集的特征维度 d=10，但是只有 m=3 或者 4 是真实特征。因为这些真实特征已经是已知的了，所以我们可以通过计算每种特征选择算法给真实特征赋予的中值等级来评估该算法的性能，较低的中值等级意味着较好的性能。

上图展示了模拟数据集上真实特征的中值等级（y 轴）随着样本量（x 轴）的变化。中值等级越低，性能越好。点画线代表最优的中值等级。

在二分类和四分类任务中，我们的方法比其他的算法有着更优的性能，我们的方法在 50 个样本以内就能够鉴别出真实特征，而其他的方法需要接近 100 个样本或者最终都无法成功收敛。在可加非线性模型中，几个算法的性能都比较好，在所有的样本大小中我们的算法都不逊色。

现实数据

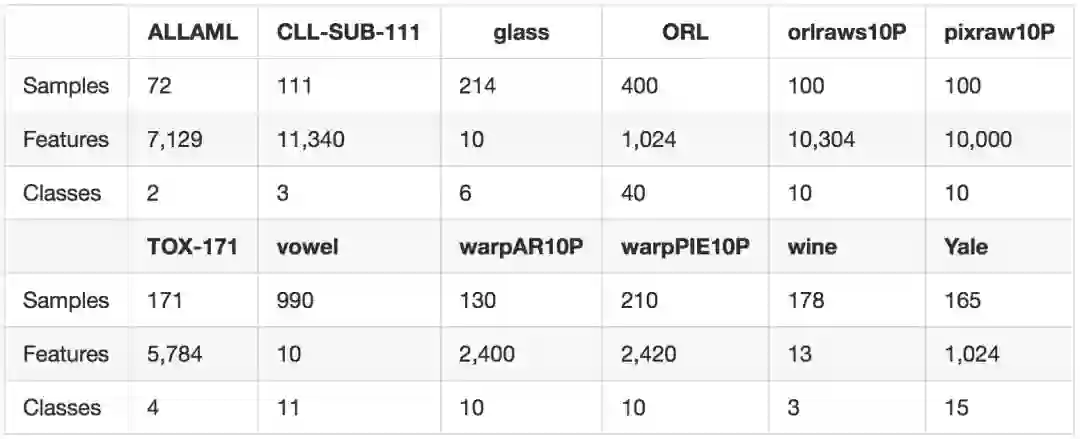
现在我们将注意力转移到现实任务中，研究我们的方法和其他几种非线性方法（mRMR、BAHSIC、MI）与核 SVM 结合使用时的下游分类性能。我们在 ASU 特征选择网站和 UCI 库中的 12 个标准基准任务上进行了实验。下表是对所用数据集的总结。

数据集来自多个领域，包括基因数据、图像数据、声音数据，而且高维度和低维度的都有。

对于每一个任务，我们运行并评估每个算法，以获取所有特征的排序。然后基于前 m 个特征训练核 SVM，计算准确率，从而评估性能。下图展示了我们的结果。

上图展示了现实基准数据集中的准确率（y 轴）随所选特征数目（x 轴）的变化。准确率越高，性能越好。

与其他三种流行的非线性特征选择方法相比，我们的方法在大多数例子中都是最强大的，有时候会有特别大的差距，例如在 TOX-171 任务中。尽管我们的方法偶尔在开始时（所选特征数目比较少时）性能会不太好，但最终还是会跟其他算法的性能持平或超越它们（glass 任务除外）。

结论

在这篇文章中，我们提出了条件协方差最小化（CCM）方法，这个方法基于最小化条件协方差算子的迹来进行特征选择。这个方法的思想是选择能够最大化预测基于协变量响应依赖的特征。我们通过将很难处理的离散协变量响应依赖松弛化，以获取适合基于梯度的优化的连续近似，从而完成该方法。我们在多个合成数据集和现实数据集上进行实验，证明了该方法的有效性，发现我们的方法通常会优于目前最先进的算法，包括另一个基于希尔伯特-施密特独立性系数（Hilbert-Schmidt independence criterion）的核特征选择方法。

更多信息

关于算法的更多信息，请参考链接中的内容：

• 论文：https://papers.nips.cc/paper/7270-kernel-feature-selection-via-conditional-covariance-minimization

• 代码：https://github.com/Jianbo-Lab/CCM

论文：Kernel Feature Selection via Conditional Covariance Minimization

摘要：我们提出了一种特征选择方法，该方法利用基于核的独立性估计找出协变量的子集，可最大化预测响应变量。我们基于之前的核降维研究构建该方法，展示了如何通过约束优化问题（涉及条件协方差算子的迹）进行特征选择。我们证实了该步骤稳定一致的结果，同时还展示了该方法在多个合成和现实数据集上与其他先进算法相比的优越性。 

原文链接：http://bair.berkeley.edu/blog/2018/01/23/kernels/

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者/实习生）：hr@jiqizhixin.com

投稿或寻求报道：editor@jiqizhixin.com

广告&商务合作：bd@jiqizhixin.com