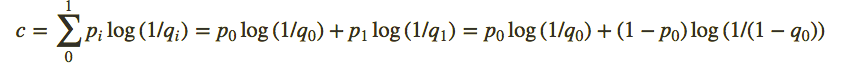一文总结熵，交叉熵与交叉熵损失

作者 | Vijendra Singh

编译 | VK

来源 | Medium

整理 | 磐创AI

交叉熵损失是深度学习中应用最广泛的损失函数之一，这个强大的损失函数是建立在交叉熵概念上的。当我开始使用这个损失函数时，我很难理解它背后的直觉。在google了不同材料后，我能够得到一个令人满意的理解，我想在这篇文章中分享它。

为了全面理解，我们需要按照以下顺序理解概念:自信息, 熵，交叉熵和交叉熵损失

自信息

"你对结果感到惊讶的程度"

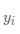
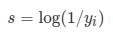
一个低概率的结果与一个高概率的结果相比，低概率的结果带来的信息量更大。现在，如果是第i个结果的概率，那么我们可以把自信息s表示为:

熵

现在我知道一个事件产生某个结果的自信息，我想知道这个事件平均带来多少自信息。对自信息s进行加权平均是很直观的。现在的问题是选择什么权重?因为我知道每个结果的概率，所以用概率作为权重是有意义的，因为这是每个结果应该发生的概率。自信息的加权平均值就是熵(e)，如果有n个结果，则可以写成:

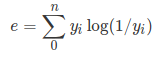
交叉熵

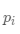
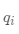
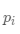
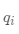
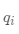
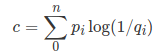
现在，如果每个结果的实际概率为却有人将概率估计为怎么办。在这种情况下，每个事件都将以的概率发生，但是公式里的自信息就要改成（因为人们以为结果的概率是）。现在，在这种情况下，加权平均自信息就变为了交叉熵c，它可以写成：

交叉熵总是大于熵，并且仅在以下情况下才与熵相同 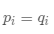，你可以观看
https://www.desmos.com/calculator/zytm2sf56e的插图来帮助理解。

交叉熵损失

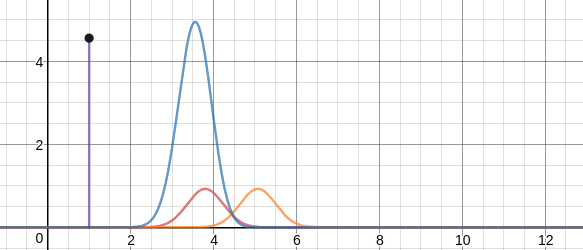
紫色线代表蓝色曲线下的面积，估计概率分布（橙色线），实际概率分布（红色线）

在上面我提到的图中，你会注意到，随着估计的概率分布偏离实际/期望的概率分布，交叉熵增加，反之亦然。因此，我们可以说，最小化交叉熵将使我们更接近实际/期望的分布，这就是我们想要的。这就是为什么我们尝试降低交叉熵，以使我们的预测概率分布最终接近实际分布的原因。因此，我们得到交叉熵损失的公式为：

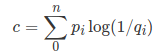
在只有两个类的二分类问题的情况下，我们将其命名为二分类交叉熵损失，以上公式变为：

---

方便交流学习，备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多： 机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐阅读：

【ACL 2019】腾讯AI Lab解读三大前沿方向及20篇入选论文

【一分钟论文】IJCAI2019 | Self-attentive Biaffine Dependency  Parsing

【一分钟论文】 NAACL2019-使用感知句法词表示的句法增强神经机器翻译

【一分钟论文】Semi-supervised Sequence Learning半监督序列学习

【一分钟论文】Deep Biaffine Attention for Neural Dependency Parsing

详解Transition-based Dependency parser基于转移的依存句法解析器

经验 | 初入NLP领域的一些小建议

学术 | 如何写一篇合格的NLP论文

干货 | 那些高产的学者都是怎样工作的？

一个简单有效的联合模型

近年来NLP在法律领域的相关研究工作

---

让更多的人知道你“在看”