优化 | 非光滑优化的光滑化

2019 年 12 月 7 日 极市平台

加入极市专业CV交流群，与6000+来自腾讯，华为，百度，北大，清华，中科院等名企名校视觉开发者互动交流！更有机会与李开复老师等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号，回复 加群，立刻申请入群~

来源：运筹OR帷幄@微信公众号

导读：

本文整理自知乎提问“在你的研究中，非光滑优化(Nonsmooth Optimization)有哪些应用？”的两个回答。第一个回答介绍了什么是Nesterov's smoothing technique，以及它在Packing LP中的应用；第二个回答补充了它在对偶分解中的应用。

截止到目前2019年底为止，这篇05年优化界巨擘Yurii Nesterov的文章smooth minimization of non-smooth functions（非光滑函数的光滑优化）已经得到了2200+引用，其经典程度可见一斑。

Nesterov一生对优化界贡献无数，而其最为出名的工作都是在当时对很多优化研究者反直觉的结果，最出名的Nesterov加速算法（Nesterov's accelerated method）先不提（几十年来人们都在试图从各种方式理解为何这个简单的算法就能“加速”了），这边我们要讲的Nesterov's smoothing也是很神奇，是说对于广泛的非光滑函数，我们可以将之光滑化并近似得到一个快得多的光滑优化里的算法求解。

一、非光滑优化的迭代复杂度下界

在具体说明之前，我们先简单讨论一下非光滑凸优化和光滑凸优化之间的迭代复杂度下界。

关于这个下界的结果也有一段有意思的历史轶闻。实际上A. Nemirovski（注意这位不是Nesterov，但也是苏联数学家，算是Nesterov早期在优化方面的导师）和D. Yudin（苏联数学家+1）早在80年代初就把各种光滑非光滑一阶算法复杂度的下界搞清楚了（[1]），然而因为他们当时在苏联（和美国这边还在冷战）然后他们的结果也都是用俄语发表在苏联国内的期刊上（然后是出版了俄语的专著），因此北美这边学术界根本不知道他们的结果，大概90年代才开始有人试图做复杂度相关的问题，后来才发现早已被苏联大佬们解决了。。。

类似下界结果的讨论和证明可见Nesterov本人去年刚刚再版的经典书（[5]），或者王奇超、文再文、蓝光辉、袁亚湘老师的中文讲义“优化算法复杂度简介”（[6]）。

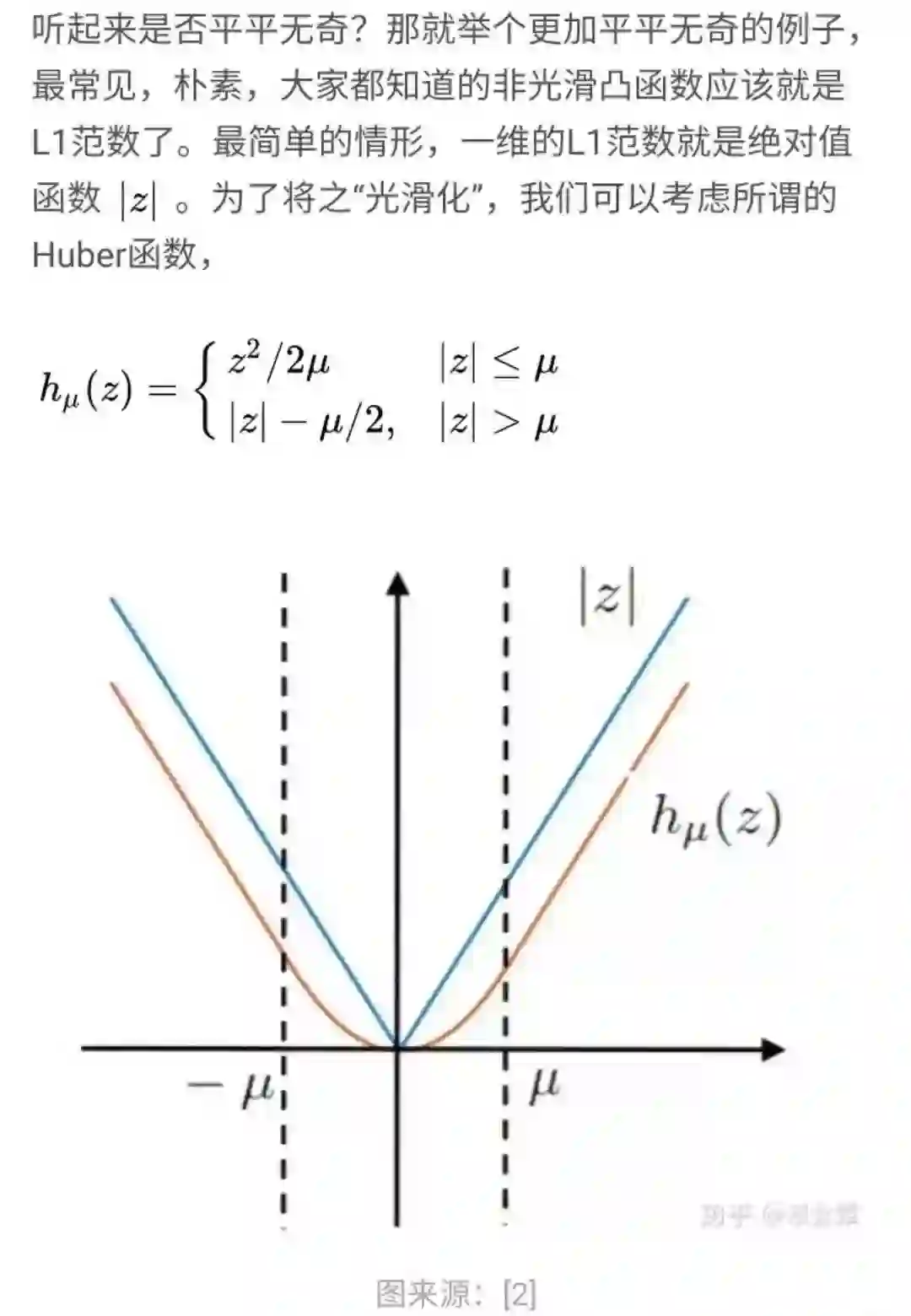
二、一个非光滑函数光滑化的例子

当然实际情况是我们往往并不只有first order oracle给的信息。在日常应用中，一般来说即使 f 非光滑我们因为知道 f 的形式，可能可以从中得到更多的“信息”。这就是Nesterov's smoothing的出发点。

三、更一般的Nesterov's Smoothing: 共轭函数和Fenchel-Legendre对偶

事实上，关于凸函数的共轭，Legendre-Fenchel Dual这些观点，我在之前的知乎的许多文章和回答里多次写过了。因此这里一些基本的概念就不再过多重复（比如strong convexity可以看成是smoothness的对偶/共轭性质；然后共轭函数的几何意义等等），想补课的同学可参考：《Fenchel-Legendre Duality观点下的优化算法们(I):前言》（https://zhuanlan.zhihu.com/p/34236792）和线性空间的对偶空间和优化里的拉格朗日对偶有什么关系？-覃含章的回答-知乎(https://www.zhihu.com/question/48976354/answer/113740571)（这些对搞优化的同学是很基础/有用的概念~）。

四、更多的应用（其一）：Packing LP

Nesterov's smoothing看起来抽象：需要找一个 d 函数算共轭似乎不太容易，但实际上它的应用非常非常广泛。Nesterov的原始paper（[3]）就讨论了matrix game和location problem的smoothing做法。之后自然是带起了一波热潮在数不尽的非光滑优化问题里产生了非常有效的新算法。这里作为结尾，我提供一个个人非常喜欢的应用，即用Nesterov's smoothing解packing和covering LP（linear program，线性规划）。

这乍一看可能很反直觉（包括前面说的matrix game），因为线性规划问题本来就是一个历史悠久的研究领域，早就有很多特制的经典算法了。然而我们会看到对于这两类特殊的LP（packing LP和covering LP），一如当年明明是为广泛凸优化设计的内点算法(interior point method)，可以在复杂度上达到一个经典LP算法无法达到的结果。

这里因为只是举例子，因为packing LP和covering LP是对称的，我们就以前者举例。

五、更多的应用（其二）：Dual Decompositio

由于原目标函数不是严格凸(strictly convex)而引起的对偶函数不光滑(non-smooth)，更准确说是不可微，使对偶分解(dual decomposition)无法直接用来分解大规模凸优化问题，我们可以用Nesterov的smoothing technique[3]搭配accelerated method[7]拯救一下，见[8]，学艺不精，一知半(不)解，欢迎大家批评指正。

1 对偶函数可微定理(Dual Function Differentiability Theorem)

这一节内容全部整理自[9]的Appendix A和C，并且以一个简单的线性约束的优化问题为例：

1.1 为什么对偶函数concave?

1.2 什么条件下对偶方程连续？

1.3 什么条件下对偶函数可微？

2. 改进版的对偶分解：Nesterov's Smoothing + Accelerated Method

2.1 Apply Nesterov's Smoothing Technique

2.2 Apply Nesterov's Accelerated Method

文章《【学界】Mirror descent: 统一框架下的一阶算法》和《优化 | Nesterov's accelerated method》写得相当精彩的，我就偷懒不写啦~

2.3 Efficiency：smoothing parameter的选取

参考文献

[1] A. Nemirovski and D. Yudin, Information-based Complexity of Mathematical Programming, Izvestia AN SSSR, Ser. Tekhnicheskaya Kibernetika (the journal is translated to English as Engineering Cybernetics. Soviet J. Computer & Systems Sci.), 1, 1983.

[2] Y. Chen, Lecture Notes (ELE522 Large-scale Optimization for Data Sience): Smoothing for Nonsmooth Optimization, Princeton University, 2019

[3] Y. Nesterov, Smooth Minimization of Non-smooth Functions, Mathematical Programming, 103(1):127-152, 2005.

[4] Z. Allen-Zhu and L. Orecchia, Nearly Linear-time Packing and Covering LP Solvers, Mathematical Programming, 175(1-2):307-353, 2019.

[5] Y. Nesterov, Lectures on Convex Optimization, 137, Springer, 2018.

[6] 王奇超，文再文，蓝光辉，袁亚湘，《优化算法复杂度分析简介》，2018.

[7] Y. Nesterov, A Method of Solving A Convex Programming Problem with Convergence Rate O(1/k^2), Doklady ANSSR (translated as Soviet Math. Docl.) 269, 543-547, 1983.

[8] I. Necoara and J. A. K. Suykens, Application of a Smoothing Technique to Decomposition in Convex Optimization, IEEE Transactions on Automatic Control, 53(11):2674-2679, 2008.

[9] D. P. Bertsekas and J. N. Tsitsiklis, Parallel and Distributed Computation: Numerical Methods, Englewood Cliffs, NJ: Prentice-Hall, 1989.

-End-

*延伸阅读

CV细分方向交流群

添加极市小助手微信（ID : cv-mart），备注：研究方向-姓名-学校/公司-城市（如：目标检测-小极-北大-深圳），即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割等极市技术交流群（已经添加小助手的好友直接私信），更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~