OpenAI用GPT-3与小学生比数学，水平达90%！60亿小模型性能翻倍，追平1750亿大模型

来源：新智元

  本文约3005字，建议阅读6分钟
本文介绍了OpenAI训练了一个系统可以解决小学数学问题，目前该方法在同样的问题上可以拿到55分，已经达到了人类小学生90%左右的水平。

【导读】近日，OpenAI训练了一个系统可以解决小学数学问题。一个9-12岁的小孩子在测试中得分为60分，而OpenAI的新方法在同样的问题上可以拿到55分，已经达到了人类小学生90%左右的水平！

还记得上小学时，被「口算天天练」里面的应用题绕晕的阴影吗？

 

来，试一道！

 

「小明每半小时喝一瓶水。一个普通的数独难题要花他45分钟。一个极难的数独需要4倍的时间。做一道极难的数独那段时间他喝了多少瓶水？」

 

不算难吧。

 

但这回，OpenAI要拿这些应用题去考考自家的当家模型，GPT-3。

 

成绩很喜人啊！

 

新方法可以解决小学数学问题，60亿参数的GPT-3采用新方法，准确率直接翻倍，甚至追平了1750亿参数，采用微调方法的GPT-3模型。

 

更重要的是，一个9-12岁的小孩子在测试中得分为60分，而采用新方法的GPT-3在同样的问题上可以拿到55分，已经达到了人类小学生90%左右的水平！

偏科的GPT-3：重文轻理

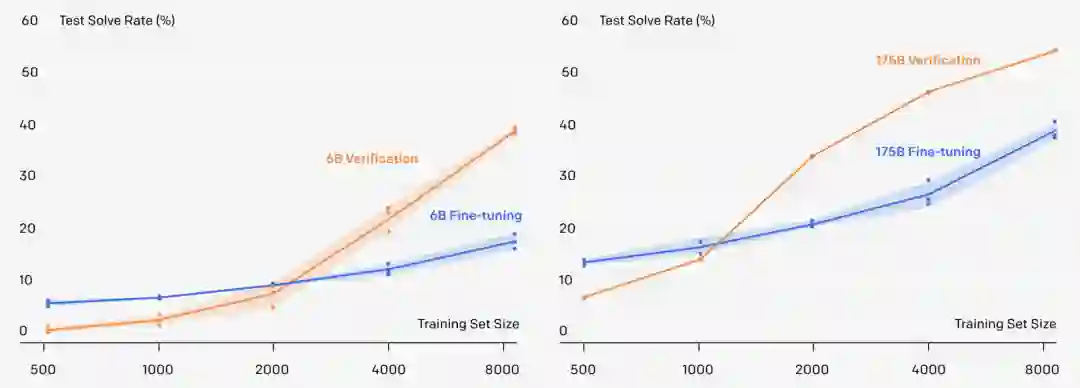
OpenAI的GPT-3以1750亿参数的「大」这一特点，让人印象颇深。

 

GPT-3「文采出众」，上知天文，下知地理。模仿名家的写作风格，展示一下广博的知识，这都不在话下。

 

然而，GPT-3这种「大」模型却是典型的偏科生，擅长文，但不擅理。

 

要是指望他们能够完成精确的多步推理，比如，解决小学数学应用题，那还是别指望了。

 

原因何在？

 

其实，问题就在于，尽管GPT-3可以模仿正确解决方法的规律，但它经常会在逻辑上产生严重错误。

 

所以，人类要想教会大语言模型理解复杂的逻辑，就必须得让模型学会识别它们的错误，并仔细选择他们的解题步骤。

 

传统方法：微调

目前，要想让大模型掌握一个领域，最常用的方法就是用大模型在指定领域微调。

 

微调通过更新模型参数进行，最小化所有训练token的交叉熵损失。显而易见，1750亿参数的模型性能要优于其他更小的模型。

 

在对不同规模的训练集进行微调后，各种GPT-3模型的测试性能

 

假设在对数线性趋势下，使用完整的GSM8K训练集时，需要一个具有10^16（10万亿）个参数的模型来达到80%的解决率。

 

然而，模型的性能并不遵循对数线性趋势，对于175B模型来说，则需要至少增加两个数量级的训练数据才能达到80%的解决率。

 

在GSM8K训练集上对6 B模型进行微调后，当模型被允许进行1次猜测（左）或100次猜测 （右）时，回答的正确率

 

其中，test@N来表示在允许模型对每个问题进行N次单独猜测时，至少正确解决一次问题的百分比。

 

test@1的性能近似单调递增，而对于test@100来说，当增加epoch的数量时，其性能比test@1的性能下降得更快。

 

选择一个具有良好覆盖率的模型是成功训练验证器的关键。从经验上看，test@100的性能在最初的几个epoch内达到了顶峰。

 

此外，在输出最终答案之前，让模型生成完整的自然语言解决方案是很重要的。如果把6B模型调整为直接输出最终答案，而不经过任何中间步骤，性能就会从20.6%急剧下降到5.2%。

 

让AI拥有「逻辑」的法宝：「验证器」

很明显，「微调」是无法让GPT-3学会逻辑推理的。

 

那这次，OpenAI是如何让GPT-3拥有「逻辑」的呢？

 

答案就是一个叫「验证器」的东西。

 

训练这个验证器（verifier），就是为了使用验证器从许多候选的解决方案中选择出最佳方案。

 

同时，为了评估「验证器」的表现，OpenAI收集了全新的「GSM8K数据集」并将其开源以方便研究。

 

论文地址：https://arxiv.org/pdf/2110.14168.pdf

GSM8K数据集地址：https://github.com/openai/grade-school-math

 

那到底「验证器」是怎么工作的呢？

 

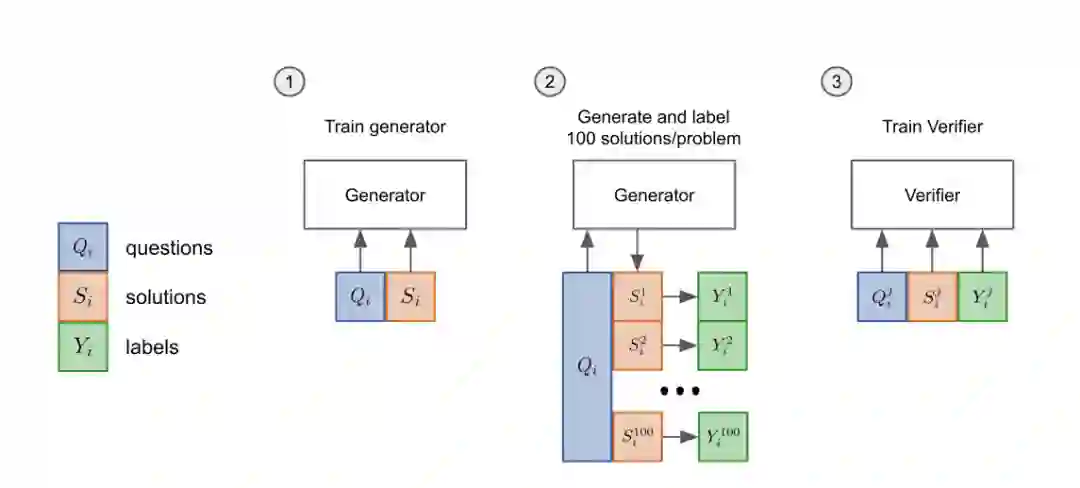
验证器：吃一堑，长一智

 

验证器（verifier）可以判断模型生成的解决方案正不正确，所以在测试时，验证器会以问题和候选解答为输入，输出每个解答正确的概率。

 

验证器（verifier）训练时，只训练解决方案是否达到正确的最终答案，将其标记为正确或不正确。但是在实践中，一些解决方案会使用有缺陷的推理得出正确的最终答案，从而导致误报。

 

 

验证器具体训练方法分为「 三步走 」:

 

1. 先把模型的「生成器」在训练集上进行2个epoch的微调。
2. 从生成器中为每个训练问题抽取100个解答，并将每个解答标记为正确或不正确。
3. 在数据集上，验证器再训练单个epoch。

 

「生成器」只训练2个epoch是因为2个epoch的训练就足够学习这个领域的基本技能了。如果采用更长时间的训练，生成的解决方案会过度拟合。

 

测试时，解决一个新问题，首先要生成100个候选解决方案，然后由「验证器」打分，排名最高的解决方案会被最后选中。

 

GSM8K数据集

 

有了新的解决方案，再来看看这次考试的「试卷」。

 

GSM8K由8500个高质量、高多样性、中等难度的小学数学问题组成。当然了。OpenAI表示，对于一个中学生来说，这些问题就都不是问题了。

 

数据集中的每个问题都需要计算2到8个步骤来得出最终答案，涉及到「加减乘除」四则运算。

 

• 高质量：GSM8K中的问题都是人工设计的，避免了错误问题的出现。

 

• 高多样性：GSM8K中的问题都被设计得相对独特，避免了来自相同语言模板或仅在表面细节上有差异的问题。

 

• 中等难度：GSM8K中的问题分布对大型SOTA语言模型是有挑战的，但又不是完全难以解决的。这些问题不需要超出早期代数水平的概念，而且绝大多数问题都可以在不明确定义变量的情况下得到解决。

 

• 自然语言解决方案：GSM8K中的解决方案是以自然语言而不是纯数学表达式的形式编写的。模型由此生成的解决方案也可以更容易被人理解。此外，OpenAI也期望它能阐明大型语言模型内部独白的特性。

 

GSM8K中的三个问题示例，红色为计算的注释

 

「微调」VS 「验证」

在GSM8K数据集上，OpenAI测试了新方法「验证」（verification）和基线方法「微调」（fine-tuning）生成的答案。

 

结果非常优秀啊！

 

在完整的训练集上，采用「验证」方法的60亿参数模型，会略微优于采用「微调」的1750亿参数模型，性能提升大约相当于模型规模整整增加30倍！

 

但大模型也不是一无是处，采用「验证」的1750亿参数模型还是比采用「验证」方法的60亿参数模型学习速度更快，只需要更少的训练问题，就能超过微调基线。

 

OpenAI发现，只要数据集足够大，大模型就能从「验证」中获得强大的性能提升。

 

但是，对于太小的数据集，验证器会通过记忆训练集中的答案而过度拟合，而不是学习基本的数学推理这种更有用的属性。

 

所以，根据目前的结果进行推断，「验证」似乎可以更有效地扩展到额外的数据。

 

举个「栗子」

 

理论都讲完了，不如来一波实操，对比一下新方法「验证」（verification）和基线方法「微调」（fine-tuning）生成的答案。

 

问题：「Richard，Jerry和Robert三个人分60个樱桃。如果Robert有30个樱桃，比Richard多10个，那么Robert比Jerry多几个？」

 

175B Verification：正确

 

175B Fine-tuning：错误

 

6B Verification：正确

 

6B Fine-tuning：错误

 

可见，新方法「验证」（verification）比基线方法「微调」（fine-tuning）在回答数学应用题上有了很大的提升。

 

不过，「验证」的方法也不是十全十美的，也有它做不对的问题。毕竟还要考虑6B小模型的局限性。

 

还记得最开始的那个问题么？

 

「John每半小时喝一瓶水。一个普通的数独难题要花他45分钟。一个极难的数独需要4倍的时间。做一道极难的数独那段时间他喝了多少瓶水？」

 

175B Verification：正确

 

175B Fine-tuning：错误

 

6B Verification：错误

 

6B Fine-tuning：错误

 

当然，如果问题再难一点儿，语言模型们就集体躺平了。

 

比如下面这个：

 

「Debra正在监测一个蜂巢，看一天中有多少蜜蜂来来往往。她看到30只蜜蜂在前6个小时内离开蜂巢，然后她看到1/2的蜜蜂在接下来的6个小时内返回。她看到两倍于第一次离开蜂巢的蜜蜂在接下来的6个小时内飞出蜂巢。然后，之前离开的每只蜜蜂，如果还没有回来，在接下来的6个小时内都会回到蜂巢。在这一天的最后6个小时里，Debra看到有多少只蜜蜂回到了蜂巢？」

 

175B Verification：错误

 

175B Fine-tuning：错误

 

6B Verification：错误

 

6B Fine-tuning：错误

 

看来，AI做数学题还是道阻且长啊。

 

你要不要也来尝试一下？

参考资料：

https://openai.com/blog/grade-school-math/

https://arxiv.org/pdf/2110.14168.pdf

—— END ——