大美之天地，将言已忘言——为何我们总用微分方程来刻画这个世界

2017 年 10 月 23 日 中科院物理所 AI Euler

任何物理理论都是在对这个世界建模，那么为何我们总用微分方程来刻画这个世界呢？

什么时候可以用微分方程来刻画世界？

归根结底，现实世界是量子的(离散的、随机的)，而非经典的(连续的、确定性的)。但我们在刻画许多问题时，却总是用确定、连续的微分方程来描述它，虽然这已牵扯了许多高维非线性系统，足够复杂难解，但其实只是一种经典极限下的近似。

我们现在想了解时间/空间上全局的性质，但如果所有的信息都需要把握，就太难了。于是我们假装自己站在其中的某一点上去感知世界对自己的影响，由此获取大致的信息，并假定这样局域的了解可以表征全局的属性，然后依此建模。这就要求所刻画的系统必须能用平均场近似比较好的来表征。

所谓平均场近似，就是把一个复杂的多体系统的演化，依据处于其中的局域的研究对象所接收的综合信息来表征的近似手段。它相当于把整个环境的作用取了积分，作用到局部的一个对象上。这一整合过程必然会平均掉一些局部的涨落，因而损失了部分信息，但使问题变得更简化，也即降低了所研究问题的维度。

一般而言，所考虑的系统粒子数越大，环境与系统的相互作用越弱，环境变化越缓慢，平均场近似就越好，采用微分方程来刻画系统的动力学就越不失真。

而若针对的是一个粒子数比较少、涨落比较大的系统，比如生命系统中的各种蛋白质之间的相互作用，一个细胞里同类分子往往一共才几十到几千个，那么平均场近似就不太恰当了。这时需要用更微观的模型去描述。比如化学里就有 Gillespie 算法等，用于模拟一大群不同的相互作用粒子在给定规则下具有随机性的演化。其每一步往另一种状态跳转的概率，都与当前的各种粒子数目分布有关。

常微分与偏微分的区别？

常微分方程(组)与偏微分方程(组)的本质区别在于所研究的动力学空间中的对象不同。

常微分方程（组）描述的是n维动力学空间中的一个点随着时间变化而演化形成的一个轨迹。

比如下图，是一个二维空间中的稳定螺旋点周围的两个点的运动随时间变化而逐渐趋于不动点所形成的两条轨迹[1]。

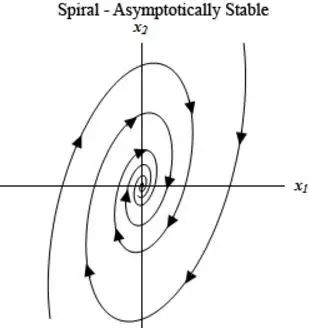
而偏微分方程（组）所刻画的是一个n维动力学空间中的一个曲线、曲面、超曲面随着时间变化而演化产生的一个变化过程。

比如下图所描述的，可以是一条曲线上各点的值随时间变化的过程[2]。

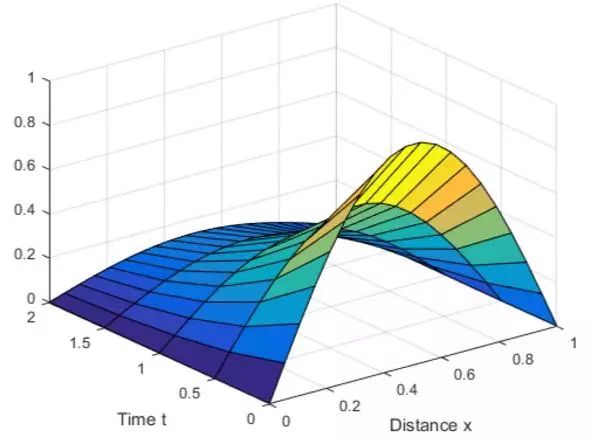
为何物理、化学方程(组)常是偏微分的呢？

因为在物理和化学等考虑实际问题的科学中，我们研究一个具体的物体的时候，关注的东西是一个多个变量的函数的变化。

比如琴弦，我们关注的东西是它作为一个整体在各处振动起来的高或低的分布情形，而不仅仅关注弦上的一个点的运动，它是时间和位置的函数，所以我们用PDE来描述这个东西所对应的动力学空间中的一个曲线的变化（一个空间的维度，一个时间的维度）。

还比如二维的反应扩散系统中的图灵斑图(如下图，是一个系统中的空间上的物质分布随时间变化而逐渐变化，形成斑图的过程[3])，我们现在关注的是某种化学物质在各处的浓度作为一个整体呈现给我们的在一个面上的分布样子（有些地方浓度高，有些地方浓度低，整体的分布呈现一定的规律）；因此我们用 PDE 来描述这个动力学空间中的曲面的变化，它在空间上需要两个维度，时间上需要一个维度。

所以，选取什么模型来刻画这个世界，取决于所研究的对象是动力学空间中一个曲线、(超)曲面随时间整体的变化，还是一个点随时间的演化轨迹，也取决于我们的能力范围。

(以下仅为个人观点，供探讨)

另一方面，也许还取决于历史经验积累与实际条件。

最初的微分动力系统理论，是在经典力学蓬勃发展的背景下发展的。众所周知，牛顿开创了一套体系相当完备的经典力学理论，而他也正是微积分的创始人之一，这部分数学与物理在那时的发展是相辅相成的。如果人们最初发展的是离散系统理论，而今我们能使用的数学手段，或许就会包含更多用于处理离散系统的工具与语言吧。在处理许多问题时，人们首先想到的是微分方程，而非离散动力学模型，这与经典理论与微积分共同发展的历史或许也是脱不开关系的。

与之类似的另一例：在量子场论中，用各种方法来计算散射截面是一项最常见的任务。这或许并非因为必然只有散射截面这一物理量值得关心，而更多地是因为：基于一直以来实验发展情况，至今为止，只有这个量是比较好测的。

References

[1]http://tutorial.math.lamar.edu/Classes/DE/PhasePlane.aspx

[2]https://cn.mathworks.com/help/matlab/math/partial-differential-equations.html

[3]Lee K C, Yu Q, Erb U. Mesostructure of Ordered Corneal Nano-nipple Arrays: The Role of 5–7 Coordination Defects[J]. Scientific Reports, 2016, 6.

来源：冰土中的新仙女木