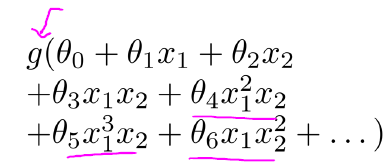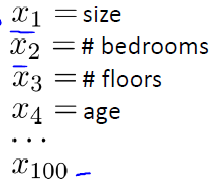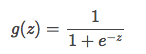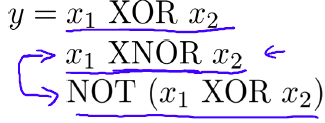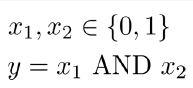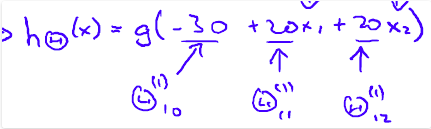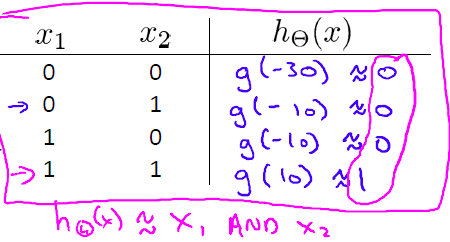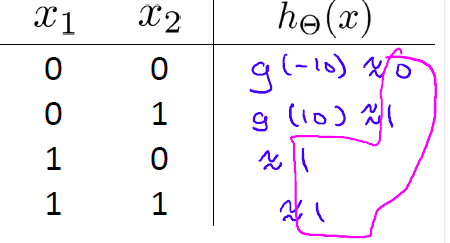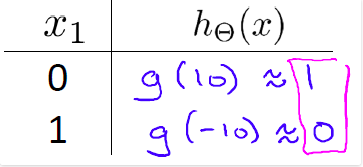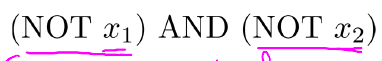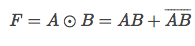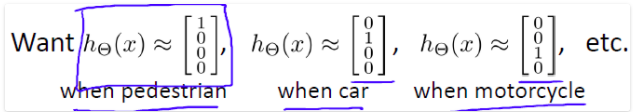推荐|斯坦福大学机器学习:神经网络的表示!
“全球人工智能”拥有十多万AI产业用户,10000多名AI技术专家。主要来自:北大,清华,中科院,麻省理工,卡内基梅隆,斯坦福,哈佛,牛津,剑桥...以及谷歌,腾讯,百度,脸谱,微软,阿里,海康威视,英伟达......等全球名校和名企。
今天主要分享斯坦福大学机器学习“神经网络的表示“学习笔记,主要包括7部分:
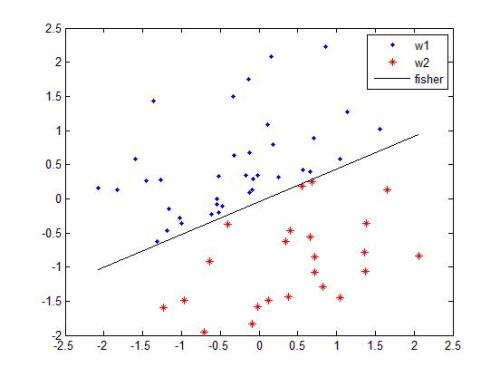
一、 非线性hypotheses:非线性分类器:之前谈过线性回归,逻辑回归,当我们遇到一些比较复杂的分类问题时,是否还有其他选择?例如,对于多项式回归:
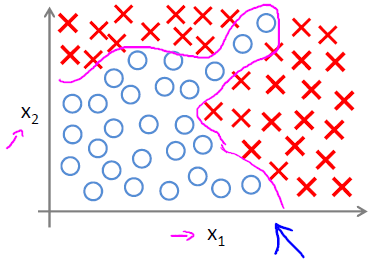
得到如下的非线性分类器:
假设这是一个房价预测问题,不过这一次不再是预测房价(回归问题),而是预测未来6个月是否能售出(分类问题)。如果有100个独立特征,例如:
那么,任取两个特征作为组合特征时,大约可以得到5000个特征( O(n2));当我们任取3个特征作为组合特征时,大约可以得到170000( O(n3)个特征.这样的问题还有很多,例如在计算机视觉的汽车检测问题中,对于一副汽车图片来说,你可以轻易的辨别出这是一辆汽车,但是在计算机或者相机“眼里”,这只是一堆像素的数字矩阵而已:
所以,对于汽车检测问题,我们需要一堆汽车图片:
和一堆非汽车图片作为训练集:
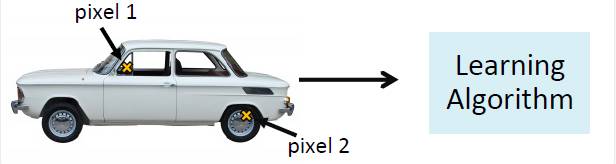
训练一个用于汽车检测的分类器,对于一个测试图片,判断是否是汽车:
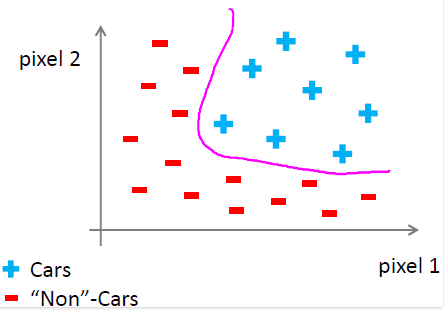
一种方法是从每辆汽车是取两个像素点作为样本的特征,然后通过学习算法来训练分类器:
那么这些正负例(汽车 or 非汽车)训练样本可以用图形表示如下:
假设每幅图片有50 * 50 = 2500个像素,那么每个样本有2500个像素点可以选择,如果是是二次项组合特征,大约有3百万个特征组合:
对于这样的有着大量特征的分类问题,除了逻辑回归,是否还有其他的学习算法?
二、 神经元和大脑
1)神经网络:
起源于尝试让机器模仿大脑的算法;
在80年代和90年代早期非常流行,慢慢在90年代后期衰落;
最近得益于计算机硬件能力,又开始流行起来:对于很多应用,神经网络算法是一种“时髦”的技术;
大脑很神奇,可以让我们去听,去看,去触,也可以做数学题,做微积分,做很多神奇的事情,要模仿大脑,似乎需要我们写很多程序来做不同的事情?但是恰恰与此相反,做这些事情仅仅需要一个学习算法。
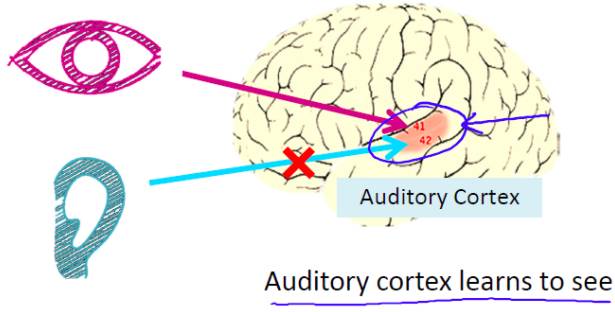
2)听觉皮层实验:
上图是大脑的一部分,红色的部分是听觉皮层,用来处理耳朵收集的声音信号并让大脑理解。神经科学家做了一个实验,切断耳朵和听觉皮层的联系,并且连接眼睛和听觉皮层,这样从眼睛采集的信号不再传送到视神经而是听觉皮层,这样做得最终结果是听觉皮层将会学习“看"。
3)体感皮层实验:
上图的红色区域是体感皮层,主要身体的触觉,与听觉皮层实验相似,如果我们做相似的实验,那么体感皮层也将学会”看“。
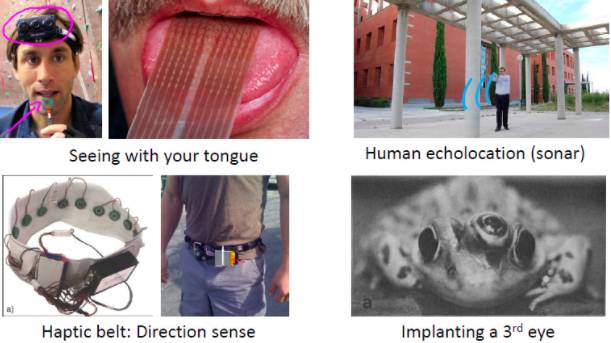
上述两个实验统称为神经重布线实验(neuro-rewiring experiments), 这些实验给我们的感觉就是同样的一块儿脑组织既可以处理视觉,也可以处理听觉,还可以处理触觉,也许就存在一种学习算法来处理视觉信号,听觉信号和触觉信号。如果我们能近似模拟或实现大脑的这种学习算法,我们就能获得绝大部分大脑可以完成的功能,因为大脑可以自己去处理不同类型的数据。以下是一些模拟大脑传感器的例子:
包括:用舌头去“看”;回声定位或者声纳定位;触觉皮带-方向感(向小鸟一样感知方向);给青蛙植入第三只眼。这些都是很酷的例子,也许人类的AI之梦并不遥远了!
三、 模型表示二:前馈网络:向量化实现
前向网络,这种网络只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号,因此被称为前馈网络。感知机( perceptron)与BP神经网络就属于前馈网络。我们已经给出了这个神经网络的模型表示,但是不够简洁,下面我们来向量化这个模型(具体的过程推荐看视频,以下仅给出总结):
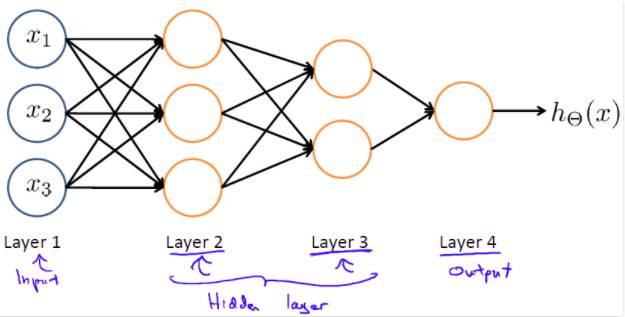
其他的网络结构:除了上述的前馈网络外,神经网络还有其他的一些网络结构,譬如:
其中第一层仍是输入层,最后一层第四层数输出层,中间两层是隐藏层。
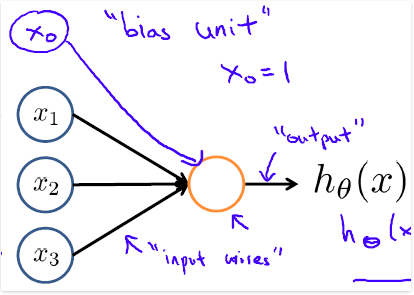
四、模型表示一:大脑中的神经元
神经网络的目标就是模拟大脑中的神经元或网络,因此在介绍hypotheses的表示之前,先让我们来看一看大脑中神经元:
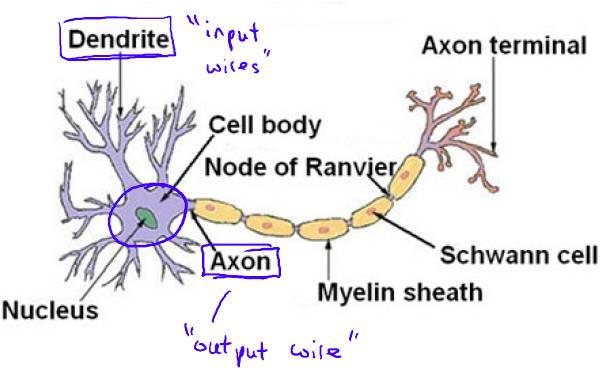
其中
x1,x2,x3
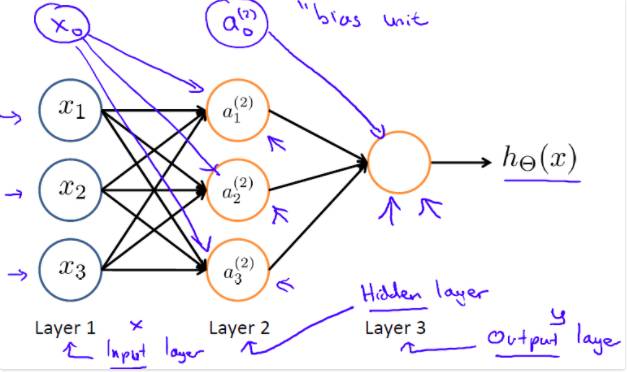
将多个神经元组织在一起,我们就有了神经网络,例如如下的三层结构的神经网络:
第一层称为输入层,第二层是隐藏层,第三层是输出层,注意输入层和隐藏层都存在一个偏置(bias unit). 其中:
五、 例子和直观解释一:这节需要提前了一下“逻辑代数”中的逻辑函数,以及非线性分类器例子-异或(XOR)/同或(XNOR)。先介绍一下同或运算和异或运算:
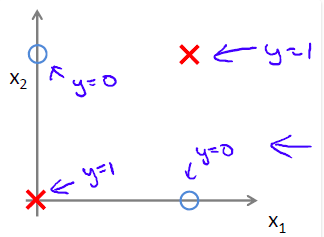
下图是一个同或预算的示例,其中
x1,x2
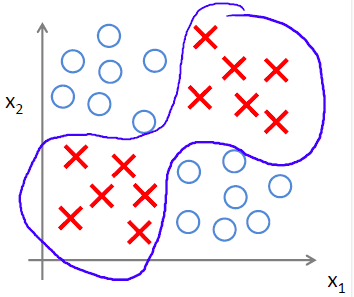
可以将其对应到一个非线性分类器,如下图所示:
同或逻辑和异或逻辑互补:
同或运算和异或运算是逻辑代数中的复合运算,因此下面我们先介绍三种最基本的逻辑运算(与逻辑运算、或逻辑运算、非逻辑运算),同时分别介绍其对应的神经网络实现,最后将这几种基本的逻辑运算组合,形成最终的同或逻辑运算的神经网络。
与(AND)逻辑运算示例:
相信大家对于与(AND)运算很熟悉,其基本的表达式如下:
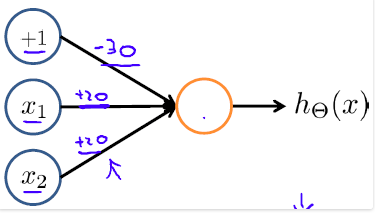
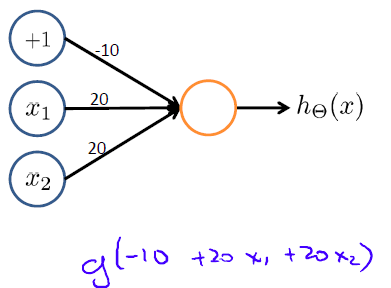
我们可以用一个简单的神经网络(一个神经元)表示与逻辑运算:
其中激活函数
hΘ(x)
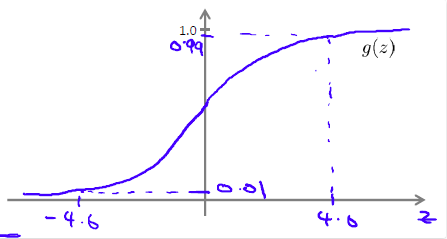
这里的激活函数是sigmoid(logistic) function,其图形表示如下:
对于g(z)来说,当z>=4.0时,g(z)约等于1;当z<=-4.0时,g(z)约等于-1. 对于上述激活函数,将二值(0, 1)变量
x1,x2
这里的神经网络激活函数
hΘ(x)
或(OR)逻辑运算示例:
我们也给出一个简单的神经网络模型来模拟或(OR)逻辑运算:
将二值(0, 1)变量
x1,x2
六、例子和直观解释二
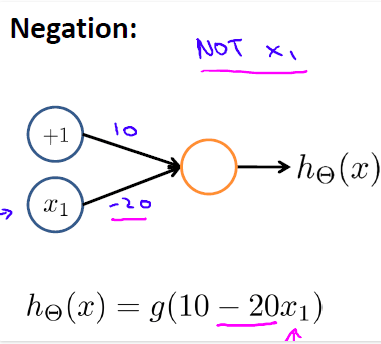
下面第三个基本的逻辑运算:非(NOT)逻辑运算:用一个简单的神经网络模型来模拟非(NOT)逻辑运算:
得到的对应表如下:
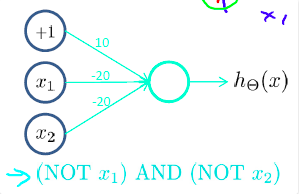
非逻辑运算仅针对一个输入值,我们来表示一个略微复杂的逻辑表达式:
这个表达式等于1的前提是”当且仅当x1=x2=0".可以用神经网络模拟如下:
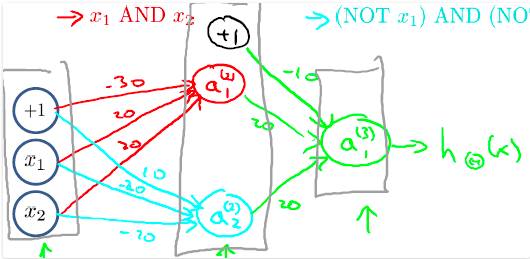
有了上述三个基本逻辑运算的基础和相关的神经网络模型表示,可以将其组合为一个略微复杂的”同或(XNOR)逻辑运算的神经网络“:
对于这个神经网络,这里稍作一点解释,同或运算的表达式如下:
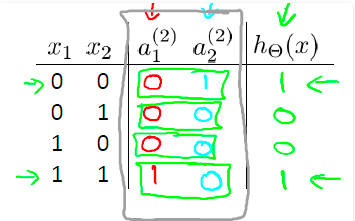
上图中第二层隐藏网络a1和a2分别代表了A And B和Not A And Not B,a1和a2又做了一次或逻辑运算就得到了同或逻辑运算。该神经网络对应的输出与同或运算的真值表相同:
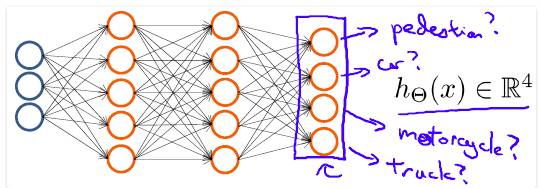
七、多类分类问题:在逻辑回归的笔记中,我们谈到了多类分类问题,而神经网络同样可以应用于多类分类问题,只不过在表达上略有区别。首先来看一个机器视觉中分类的例子:
对于一个输入图片,需要识别其属于行人、轿车、摩托车或者卡车中的一个类型,这是一个多类分类的问题。用神经网络表示如下:
其中输出 hΘ(x)是一个4维向量,如下表示:
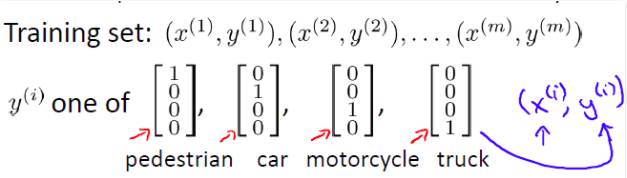
当向量的某个元素为1,其他为0时,代表分类结果为某个为1元素所对应的类别。这与之前逻辑回归中的多类分类表示不同,在逻辑回归中,输出y属于类似于{1, 2, 3,4}中的某个值,而非一个向量。因此,如果要训练一个多类分类问题的神经网络模型,训练集是这样的:
特别注意 y(i)是一个向量。
AI专家问答平台