学界 | 从数学概念入手，一文带你理解感知机是什么

AI科技评论按：神经网络已经成为了人工智能最火的领域，是源于大脑结构的计算模型。 属于信息处理结构，其最重要的属性是其从数据中学习的能力。 这些技术在营销、工程等诸多领域取得了巨大的成功。

感知机是一种人工神经网络，由Frank Rosenblatt于1957年发明，他也提出了相应的感知机学习算法。

神经网络类型众多，其中最为重要的是多层感知机。 多层感知机中的特征神经元模型称为感知机。本文将解释从数学概念上理解感知机模型。

感知机元件

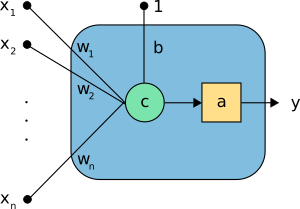
神经元是神经网络的主要组成部分，感知机是最常用的模型。 如下图所示。

上述神经元包含下列元素：

•  输入（x1 ，...，xn ）。

• 偏移b和突触权重（w1 ，...，wn ）。

• 组合函数c（·）。

• 激活函数a（·）。

• 输出y。

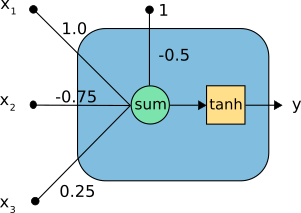
如下图所示的神经元有三个输入。 它将输入集合x =（x1 ，x2 ，x3 ）变换为单个输出y。

上图中的神经元，包含下列元素：

• 输入（x1 ，x2 ，x3 ）。

• 神经元参数，为集合b = -0.5和w =（1.0，-0.75,0.25）。

• 组合函数c（·），将输入与偏移和突触权重合并。

• 激活函数设置为双曲正切tanh（·），通过该组合生成神经元输出。

• 输出y。

神经元参数

神经元参数由偏移和一组突触权重组成。

• 偏置b是实数。

• 突触权重w =（w1 ，...，wn ）是大小为输入数量的向量。

因此，该神经元模型中的参数的总数是1 + n，其中n是神经元中输入的数量。

上图所示的感知机。 其神经元模型包含1个偏移和3个突触权重：

• 偏移为b = -0.5。

• 突触权重向量是w =（1.0，-0.75,0.25）。

该神经元参数数量为1 + 3 = 4。

组合功能

组合函数通过输入向量x生成组合值或净输入c。 感知机中，组合由偏移加上突触权重和输入的线性组合计算得到，

c = b +Σwi·x i i = 1，...，n。

注意，偏置对激活函数净输入的增减取决于其正负。 偏移有时被表示为连接到固定为+1的输入的突触权重。

上例中的神经元，输入向量x =（-0.8,0.2，-0.4）的感知机的组合值为

c = -0.5 +（1.0·-0.8）+（-0.75·0.2）+（0.25·-0.4）
= -1.55

激活功能

激活函数通过组合来定义神经元的输出。实践当中，可以考虑多种适用的激活函数。 三个最常用的是逻辑，双曲正切和线性函数。 在此不考虑不可导出的其他激活函数，如阈值。

逻辑函数具有S形形状。 该激活是单调的新月形函数，其在线性和非线性行为之间表现出良好的平衡。 定义为

a = 1 /（1 + exp（-c））

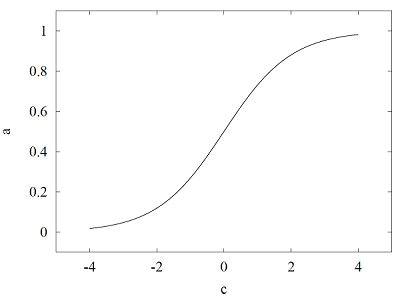
逻辑函数如下图所示。

逻辑函数的取值区间为（0,1）。 特别适合分类应用，因为输出可以根据概率解释。

双曲正切也是神经网络领域中常用的S形函数。 它非常类似于逻辑函数。 主要区别是双曲正切的取值区间为（-1,1）。 双曲正切由

a = tanh（c）

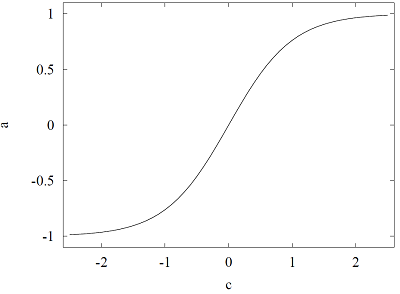
双曲正切如下图所示。

超实体正切函数非常适用于近似应用。

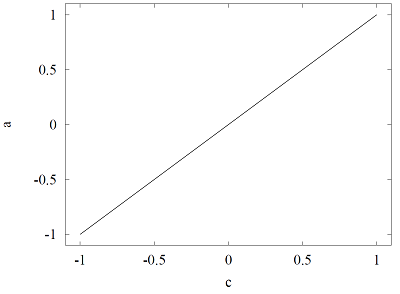
线性激活函数满足下列等式

a = c

因此，具有线性激活函数的神经元的输出等于其组合。 线性激活函数图形如下图所示。

线性激活函数也非常适用于近似应用。

本文给出的例子中，组合值为c = -1.55。 因该函数为双曲正切，所以该神经元的激活如下：

a = tanh（-1.55）
= -0.91

输出功能

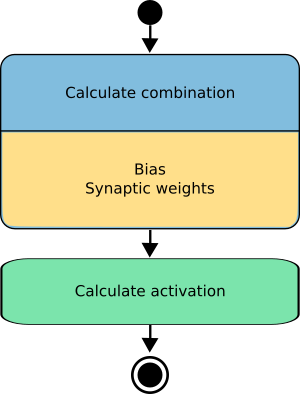
输出计算是感知机中最重要的功能。 对于特定的一组神经元输入信号，通过组合生成输出信号。 输出函数以组合和激活函数的组成表示。 下图说明了感知机中信息是如何传播的。

因此，神经元的输出最终表述为其输入的函数

y = a（b + w·x）

本文中的感知机， 如果输入x =（-0.8,0.2，-0.4），输出y如下

y = tanh（-0.5 +（1.0·-0.8）+（-0.75·0.2）+（0.25·-0.4））
= tanh（-1.55）
= -0.91

显而易见，输出函数合并了组合和激活函数。

结论

神经元是生物神经系统中单个神经元行为的数学模型。

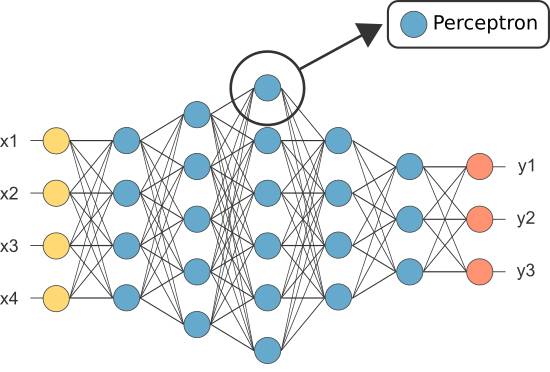
单个神经元可以完成一些非常简单的学习任务，但是许多神经元构成的网络威力巨大。人工神经网络的结构是指神经元的数量和它们之间的连接关系。 下图显示了神经元的前馈网络架构。

虽然通过本文读者能够了解感知机的功能，但是存在特征各异并且用途不同的神经元模型。如可伸缩神经元，主成分神经元，非伸缩神经元或概率神经元。上图中，可伸缩神经元为黄色，非伸缩神经元为红色。

via neuraldesigner

AI科技评论招聘季全新启动！

很多读者在思考，“我和AI科技评论的距离在哪里？”，答案就是：一封求职信。

AI科技评论自创立以来，围绕学界和业界鳌头，一直为读者提供专业的AI学界，业界，开发者内容报道。我们与学术界一流专家保持密切联系，获得第一手学术进展；我们深入巨头公司AI实验室，洞悉最新产业变化；我们覆盖A类国际学术会议，发现和推动学术界和产业界的不断融合。

而你只要加入我们，就有机会和我们一起记录这个风起云涌的人工智能时代！

如果你有下面任何两项，请投简历给我们：

＊英语好，看论文毫无压力

＊计算机科学或者数学相关专业毕业，好钻研

＊新闻媒体相关专业，好社交

＊态度好，学习能力强

简历投递：lizongren@leiphone.com