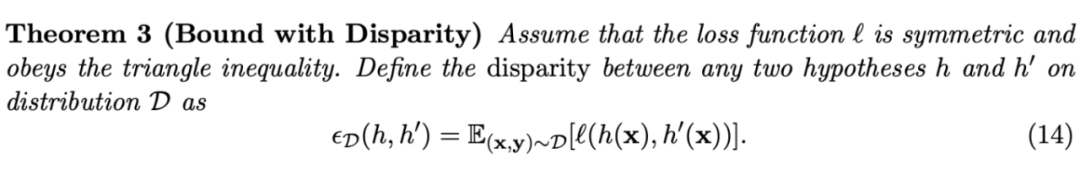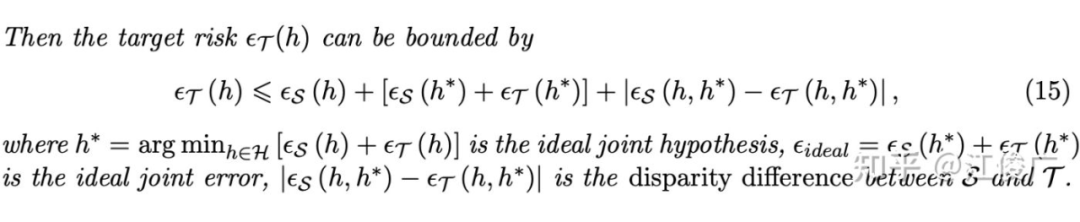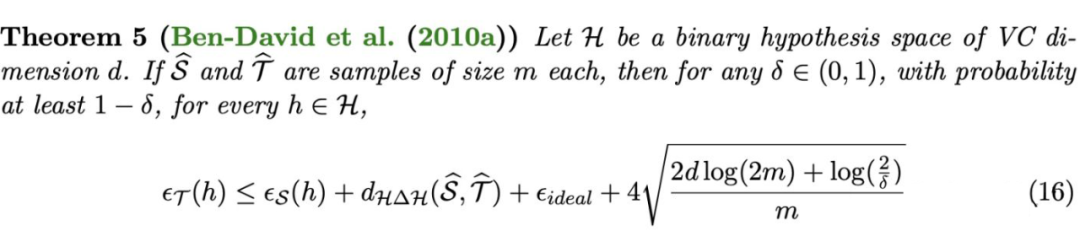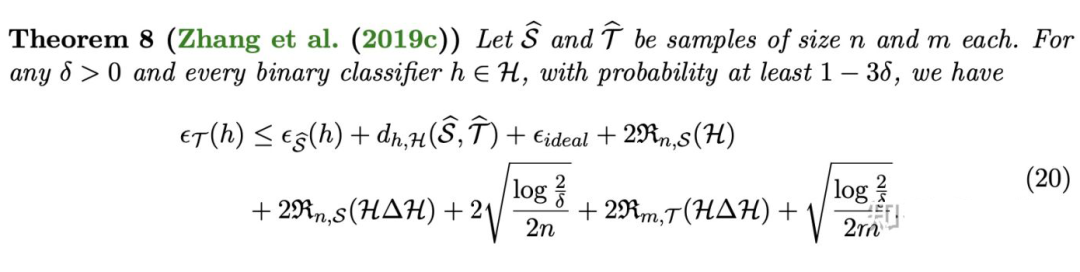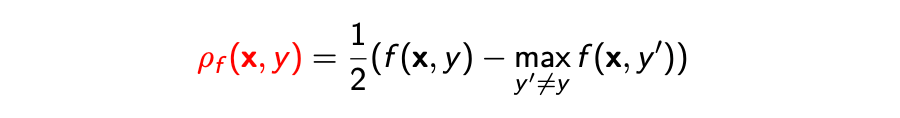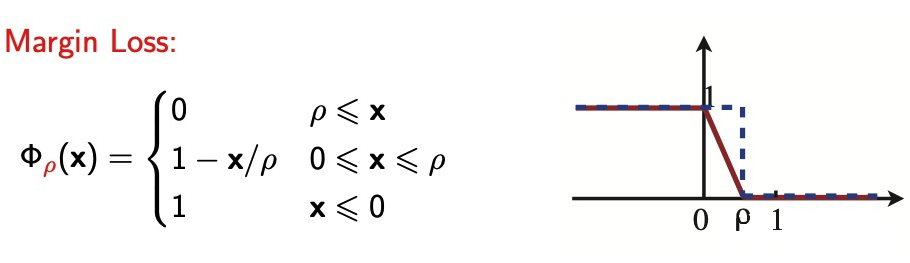迁移学习之域自适应理论简介（Domain Adaptation Theory）

©作者 | 江俊广

单位 | 清华大学

研究方向 | 迁移学习

本文主要介绍域自适应（Domain Adaptation）最基本的学习理论，全文不涉及理论的证明，主要是对部分理论的发展脉络的梳理，以及对理论的直观解释，目的是：

1. 通过这些分析启发后续域自适应算法的设计；

2. 帮助读者分析域自适应算法在具体应用中失效的原因，并提供一些改进的思路。

阅读本文前，你需要了解最基本的学习理论，包括：

• 泛化误差界（Generalization Bound ）
• 概率近似正确（PAC Learning）
• Rademacher 复杂度 [1]

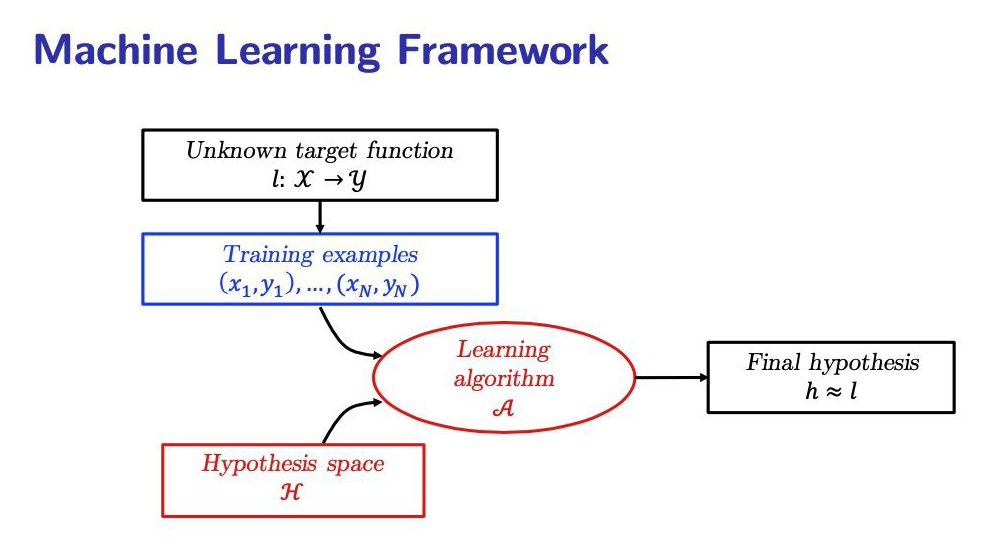
问题描述

机器学习的基本问题是，给定若干训练样本，设计一个学习算法 ，在一个函数空间 中，找到最接近目标函数的函数 。

▲ 机器学习一般的训练框架

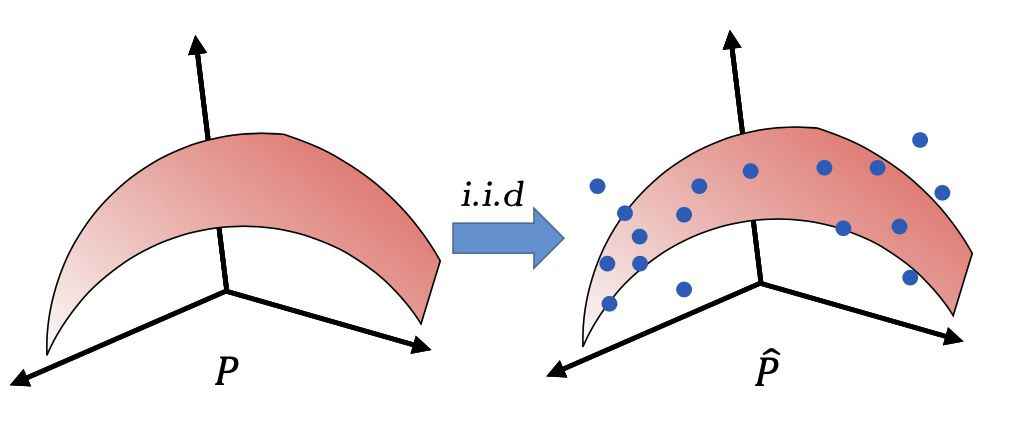
其中，监督学习（Supervised Learning）通常有一个很强的假设——独立同分布假设（independent and identically distributed, i.i.d.），即所有的训练数据和测试数据都是从同一个未知的数据分布中独立采样出来的。

▲ 独立同分布假设

独立同分布的假设使得在训练数据集上得到的函数 在测试集上的误差是能被界定（bounded）的，比如

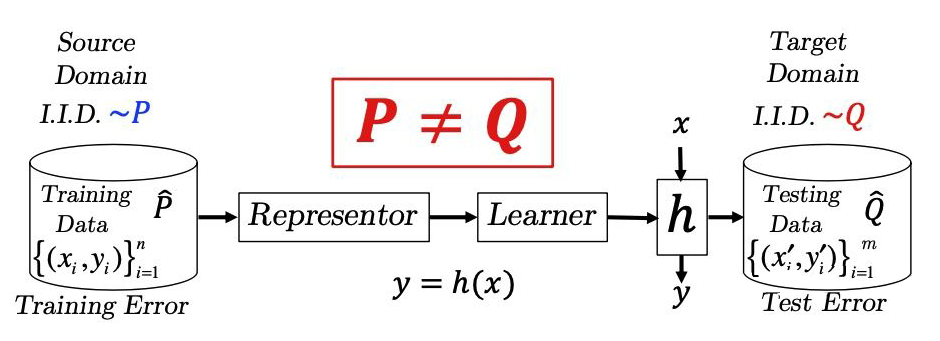
这个假设保证了一定范围内的机器学习模型是可用的，然而它也限制了机器学习的适用范围。独立同分布假设往往只存在于人工打标和清洗过的数据集上，而在大部分的生产实践中很难得到满足。图学习（Graph Learning）尝试解决数据的生成不符合独立假设的情况，而域自适应（Domain Adaptation）则尝试解决数据分布不一致的情况。

在标准的域适应问题中，存在一个有标注数据的源域（Source Domain） 和一个只有无标注数据的目标域（Target Domain） ，学习算法的目标是在函数空间 找到使得目标域泛化误差 尽可能小的函数，其中 是一个损失函数。

▲ 域自适应问题设定

域自适应的理论

2.1 理论出发点

域自适应理论最核心的想法就是如何将目标域上的泛化误差和源域上的泛化误差联系在一起。那么通过降低源域上的误差，就能间接地降低目标域上的误差。

首先，定义函数 和 在数据分布 上的差异（Disparity） [2]

首其中，差异 是泛化误差 的推广（泛化误差中 就是目标函数，因此可以忽略不写）。

然后，只需要使用泛化误差的定义以及三角不等式，我们就可以将目标域误差与源域误差联系起来。

上述不等式是目前大部分域自适应理论的出发点，它表明目标域误差除了和源域误差有关，还和两个因素有关：

• 源域和目标域上的最优联合误差（Ideal Joint Error），即 中最优的函数在源域和目标域上的泛化误差。它与假设空间的大小相关，当假设空间比较小时（比如浅层神经网络）， 中可能不存在一个函数能够同时应对两个不同分布的数据域。在域自适应理论中，通常认为函数空间足够大（比如采用深度网络），从而使得最优联合误差可以忽略不计。但是在实际应用中，这个假设不一定成立。
• 源域和目标域上的差异分歧（Disparity Difference），即 Disparity 在源域和目标域上的分歧，它刻画了不同数据域之间的距离，而大部分域自适应理论的出发点就是估计并缩小不同数据域之间的差异分歧。由于 Disparity 是定义在 和 上的，而最优函数 是未知的，因此差异分歧无法直接计算。

而不同域自适应理论的区别就在于它们是差异分歧不同的上界（Upper Bound）。

2.2 经典理论 -Divergence

-Divergence [3]  是最早的域自适应理论工作，也是目前用的最多的一个理论，比如著名的 Domain Adversarial Neural Network（DANN） [4] 就是基于这个理论。

它的想法非常简单，就是让差异分歧 在 和 所在的函数空间 求上界。

取上界的操作尽管很直观，但是通常很难进行计算和优化。因此，实际计算时还会引入一个域判别器（Domain Discriminator） ，判别器的任务是将源样本和目标样本区分开。这里的潜在假设是，判别器的函数空间 足够丰富，使得它能完全包含 ，即 。

此时 就可以被 进一步界定住。

为了让 成立，通常会使用多层感知器（MLP）来作为域判别器（理论上，MLP 是任何函数的通用逼近器）。

域判别器的准确率，刻画了源域和目标域之间的分布距离。下面的定理基于 -Divergence 给出了域自适应理论最早的泛化误差界。

其中最后一项表明，尽管目标域上的数据都是无标注的，但是目标域上的训练样本数 也会影响目标域的泛化误差。原因 -Divergence 只能在训练样本上进行估计，当 较小时， -Divergence 的估计不够准确，导致目标域上的泛化误差上界也会变大。

需要指出的是，上述定理成立的大前提是二分类问题以及 0-1 损失。在实际应用中使用域判别器计算并优化分布距离时，

• 如果损失函数是分类问题常用的交叉熵损失函数，理论上没有保证，实验上大部分时候有效。

• 如果损失函数是回归问题常用的 L1 损失或者 L2 损失，理论上没有保证，实验上一般无效。

2.3 返璞归真 Disparity Discrepancy

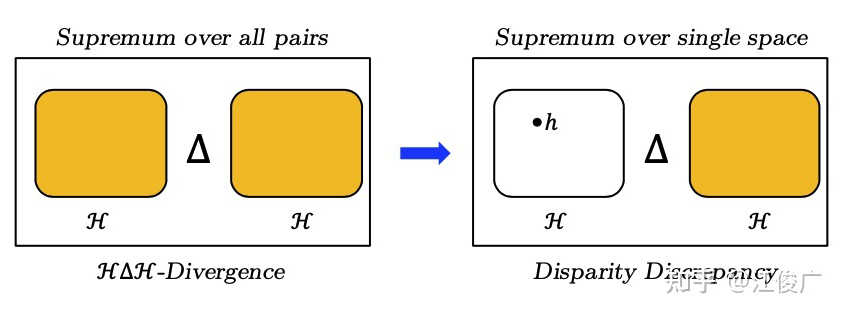
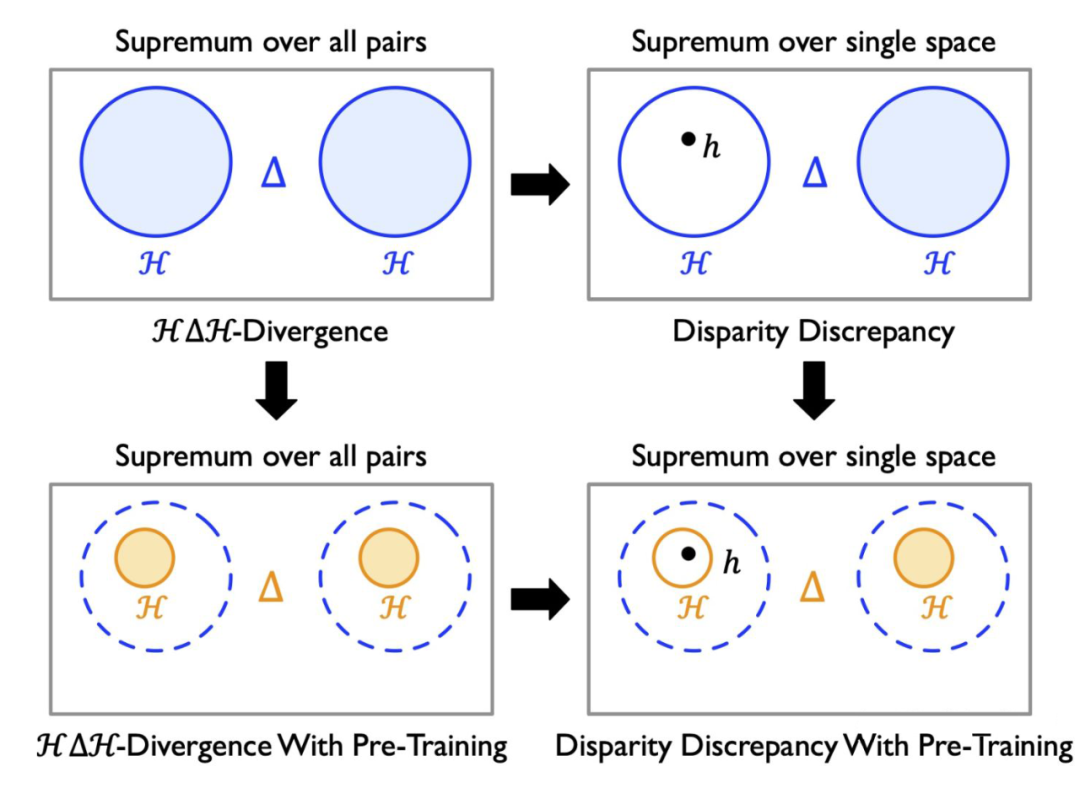
为了求差异分歧 的上界， -Divergence 同时对 和 求上界。

但这其实这是没有必要的，因为 是已知的，就是当前的函数，同时对 和 求上界反而让上界变松了。

因此差异散度（Disparity Discrepancy）[5] 的想法更加简单，就是让差异分歧只对 求上界。

下图是一个可视化的对比，橙色的区域表示取上界的函数空间。

▲ H△H-Divergence和 Disparity Discrepancy的对比

因此，理论上 Disparity Discrepancy 提供了比 -Divergence 严格更紧的差异分歧上界。

Disparity Discrepancy 更好的一个性质是，它并不限制在 0-1 损失函数上。比如对于 L1 损失函数而言，理论上只需要如下定义，Disparity Discrepancy 就可以扩展到回归问题

而且实验上也有明显的效果：

https://github.com/thuml/Transfer-Learning-Library/tree/master/examples/domain_adaptation/image_regression

2.4 间隔理论Margin Disparity Discrepancy

在分类问题中，交叉熵损失函数相比于 0-1 损失函数，一个重要的性质是，它在训练准确率为 100% 的时候依然存在损失。即使训练集的准确率没有变化（也就是 0-1 损失没有变化），当交叉熵损失下降时，测试集上的错误率也能随之下降。为了解释这个现象，学术界基于提出了间隔学习理论（Margin Theory）。

评分函数（scoring function） 的间隔（Margin）的定义是

它描述了函数 将数据 预测为类别 而不是其他类 的信心间隔。

间隔损失（Margin Loss）的含义是，只有当间隔大于某个阈值 时，损失才降为 0。因此间隔损失具有和交叉损失函数类似的性质，所以常被用于理论分析中。

为了应对多分类问题的交叉熵损失函数，间隔差异散度（Margin Disparity Disparity）[5] 将 Disparity 相关的概念扩展到带间隔的版本。

下面的定理基于间隔差异散度，给出了域自适应理论第一个针对多分类问题的泛化误差界：

从这个泛化误差界，我们能得到的结论包括：

1. 增大源域的样本数 和目标域的样本数 可以降低目标域上的泛化误差。

2. 合理控制函数空间 的大小，能够降低目标域上的泛化误差（ 也不能太小，否则最优联合误差 可以忽略的假设不再成立）。

3. 类别数 的增加会导致目标域上泛化误差的增大。

4. 一定范围增大间隔 的大小，可以降低目标域上的泛化误差（在实际使用 MDD 算法时，这也是最重要的超参数）。

实际问题中的理论分析

在理解了上述域自适应理论后，我们现在来分析一些实际应用中的问题。

3.1 回归问题中的域自适应

回归问题是域自适应理论和应用都解决得还不够好的问题。

一个简单的想法是，能不能将回归任务离散化，转化成若干个区间的分类任务，然后就可以套用原先针对分类问题的域自适应理论？

答案是否定的。定理 10（间隔差异散度）已经告诉我们，目标域上的泛化误差界和类别数 的平方正相关。而常见的回归任务，比如关键点检测中，一般会将输出空间分成 64x64 的大小，此时类别数是 4096，因此大大增加了泛化误差界。

定理 10 也给出了降低目标域上泛化误差界的手段，比如增加样本数量，或者降低函数空间的大小。例如 Regressive Domain Adaptation（RegDA） [6] 引入了空间概率分布来描述输出空间的稀疏密度，并用它来指导差异散度的估计，从而在期望的意义上，降低函数空间的大小，避免过大的泛化误差界。

https://zhuanlan.zhihu.com/p/356227636

3.2 域自适应与预训练

基于域自适应理论的深度迁移学习算法，总是使用预训练模型，而很少有从头训练的。

原因在于，深度网络的函数空间 非常大，这使得 -Divergence和差异散度中的上确界失去意义。

而预训练过程可以有效地降低允许的函数空间（Allowed Hypothesis Space） [7] ，从而大大降低目标域上的泛化误差。

▲ 预训练对于H△H-Divergence和 Disparity Discrepancy的影响

这个结论至少有两个用处：

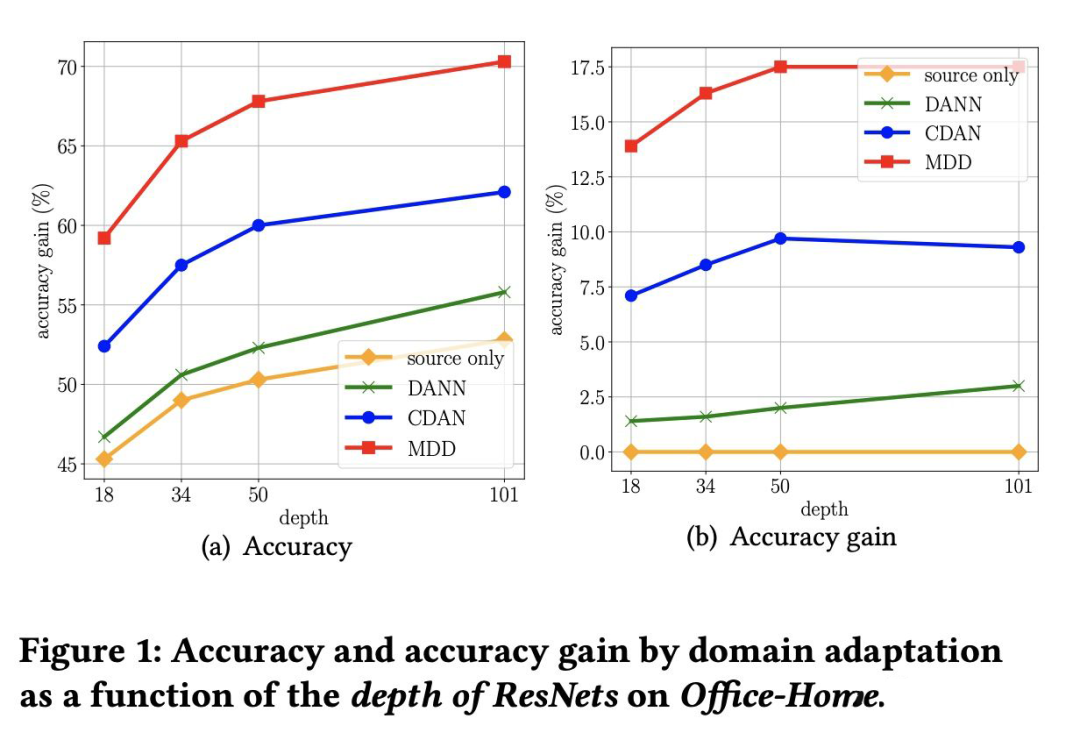
1. 当下游任务和预训练任务差异较大时，为了降低允许的函数空间，一种有效的策略是先在源域上进行预训练，然后再迁移到目标域。（这也是 RegDA [6] 采用的策略）；

2. 经过预训练后，小模型允许的函数空间反而比大模型大，导致在越大的模型上进行域自适应获得的增益越大（REDA [8] 观察到的实验现象）。因此实践中一种有效的策略是，先用大模型进行域自适应，然后将迁移得到的大模型的知识蒸馏到小模型上。

本文主要参考 Transferability in Deep Learning: A Survey [9] 中的章节 3.2.0 Domain Adaptation Theory，以及清华大学龙明盛老师的迁移学习理论讲座：

http://ise.thss.tsinghua.edu.cn/~mlong/doc/transfer-learning-theories-algorithms-open-library-ijcai

感兴趣的读者可以阅读原文：

https://arxiv.org/abs/2201.05867

链接

文献综述：

https://arxiv.org/pdf/2201.05867.pdf

Paper List：

https://github.com/thuml/Awesome-Transfer-Learning

算法库Github：

https://github.com/thuml/Transfer-Learning-Library

算法库网站：

https://transfer.thuml.ai/

参考文献

[1] Peter L. Bartlett and Shahar Mendelson. Rademacher and gaussian complexities: Risk bounds and structural results. In JMLR, 2002.

[2] Shai Ben-David, John Blitzer, Koby Crammer, and Fernando Pereira. Analysis of repre- sentations for domain adaptation. In NeurIPS, 2006.

[3] S. Ben-David, J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, and J. W. Vaughan. A theory of learning from different domains. Machine Learning, 79, page 151–175, 2010a.

[4] Yaroslav Ganin and Victor Lempitsky. Unsupervised domain adaptation by backpropaga- tion. In ICML, 2015.

[5] abYuchen Zhang, Tianle Liu, Mingsheng Long, and Michael Jordan. Bridging theory and algorithm for domain adaptation. In ICML, 2019c

[6] abJunguang Jiang, Yifei Ji, Ximei Wang, Yufeng Liu, Jianmin Wang, and Mingsheng Long. Regressive domain adaptation for unsupervised keypoint detection. In CVPR, 2021.

[7] Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic dimensionality explains the effectiveness of language model fine-tuning. In ACL, 2021.

[8] Junguang Jiang, Ximei Wang, Mingsheng Long, and Jianmin Wang. Resource Efficient Domain Adaptation

[9] Junguang Jiang, Yang Shu, Jianmin Wang, Mingsheng Long, Transferability in Deep Learning: A Survey https://arxiv.org/abs/2201.05867

特别鸣谢

感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·