MIT发布加强版「高数」求解器：7门课程正确率达81%

---

  新智元报道  

编辑：LRS

【新智元导读】MIT最近更新了他们的高等数学的求解器，通过程序合成的方式在七门大学数学课程中正确率达到了81%！而且还能对求解过程进行解释、绘图，还能生成新问题！

不光玩小学数学应用题，AI已经开始攻克高数了！

 

最近MIT的研究人员宣布他们基于OpenAI Codex预训练模型，在 本科生级别的数学问题 上通过few-shot learning成功达到81%的正确率！

 

论文链接：https://arxiv.org/abs/2112.15594

代码链接：https://github.com/idrori/mathq

 

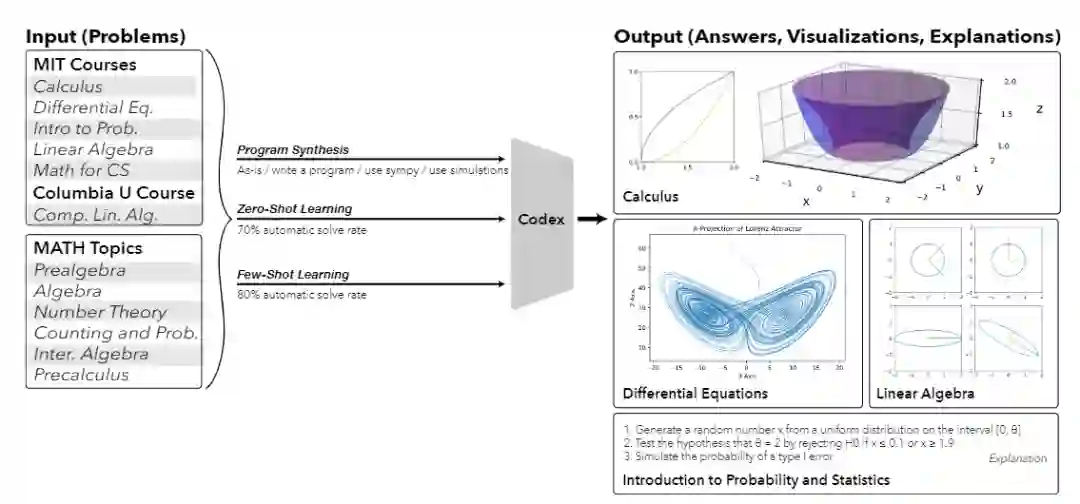
先来几个小问题看看答案，比如计算单变量函数的图形绕轴旋转产生的体积、计算洛伦茨吸引子及投影、计算和描绘奇异值分解（SVD）的几何形状，不光能正确解答，还能给出对应的解释！

 

 

确实是逆了天了，忆往昔，高数及格都是飘过，如今AI一出手就能拿81分，我单方面宣布AI已经超越人类了。

 

 

更牛的是，除了能解决普通机器学习模型难以解决的问题外，这项研究还表明该技术可以大规模推广，可以解决所属课程及类似的课程问题。

 

这也是历史上首次，单个机器学习模型能够解决如此大规模的数学问题，而且还能对问题的解答过程进行解释、绘图，甚至还能生成新问题！

 

实际上这篇论文早在年初就发布出来了，经过半年的修改后，从114页的篇幅增加到181页，能解决的数学问题更多了，附录的编号从A-Z直接拉满。

 

 

文章的作者单位主要有四个，分别为麻省理工学院、哥伦比亚大学、哈佛大学和滑铁卢大学。

 

第一作者Iddo Drori是MIT的电气工程与计算机科学系AI部门讲师、哥伦比亚大学工程和应用科学学院的兼任副教授。曾获得CCAI NeurIPS 2021最佳论文奖。

 

 

他的主要研究方向为教育机器学习，即试图让机器解决，解释和生成大学级数学和STEM课程；气候科学的机器学习，即根据数千年的数据预测极端气候变化并监测气候，融合多学科的工作来预测大西洋多年来海洋生物地球化学的变化；自动驾驶的机器学习算法等。

 

他也是剑桥大学出版社出版的The Science of Deep Learning的作者。

 

高等教育里程碑

 

在这篇论文之前，大部分研究人员都认为神经网络无法处理高数问题，只能解决一些简单的数学题。

 

即便Transformer模型在各种各样的NLP任务中超越人类的性能，在解决数学问题上仍然没有不行，主要原因还是因为各种大模型如GPT-3都是只在文本数据上进行预训练。

 

后来有研究人员发现，以逐步解析的方式（chain of thoughts）还是可以引导语言模型来推理回答一些简单的数学问题，但高等数学问题就没这么容易解决了。

 

 

当目标瞄准为高数问题后，首先就得搜集一波训练数据。

 

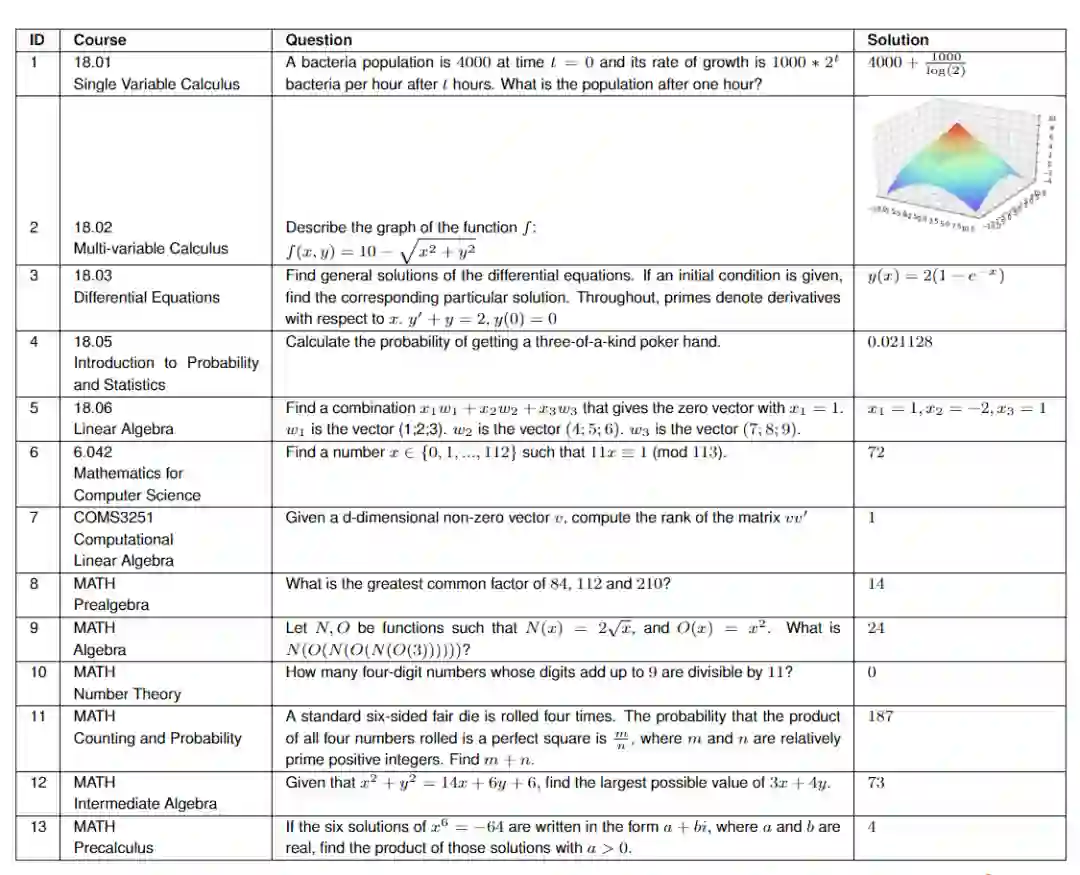
作者从麻省理工学院的七门课程中各随机抽出25个问题，包括

• 18.01单变量微积分
• 18.02多变量微积分
• 18.03微分方程
• 18.05概率和统计学概论
• 18.06线性代数
• 6.042计算机科学数学
• 哥伦比亚大学的COMS3251计算线性代数

 

对于MATH数据集，研究人员从数据集的六个主题（代数、计数与概率、中级代数、数论、预代数和预科）中随机抽取15个问题。

 

为了验证模型生成的结果不是对训练数据的过拟合，研究人员选择了没有在互联网上公开过的COMS3251课程来验证生成结果。

 

 

工作流程

 

模型以一个课程问题作为输入，然后对其进行上下文增强（automatic augmentation with context），结果合成程序（resulting synthesized program），最后输出答案和生成的解释。

 

对于不同的问题来说，输出结果可能不同，比如18.01的答案为一个方程式，18.02的答案为一个布尔值，18.03和18.06的答案为一个图或矢量，18.05的答案为一个数值。

 

 

拿到一个问题，第一步就是让模型找到问题的相关的上下文。研究人员主要关注Codex生成的Python程序，所以在问题前加上「write a program」的文字，并将文字放在Python程序的三个引号内，装作是程序里的一个docstring

 

生成程序后，还需要一个Codex prompt来指定引入哪些库，作者选择在问题前加入「use sympy」字符串作为上下文，指定为解决问题而合成的程序应该使用这个包。

 

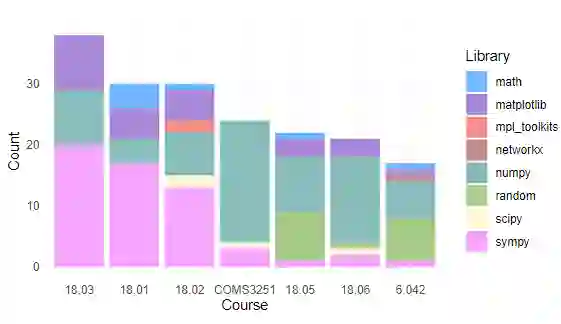
通过统计每门课程所使用的Python编程包，可以看到所有课程都使用NumPy和Sympy。Matplotlib只在有需要绘图的问题的课程中使用。大约有一半的课程使用math、random和SciPy。在实际运行的时候，研究人员只指定SymPy或绘图相关的包导入，其他导入的包都是自动合成的。

 

 

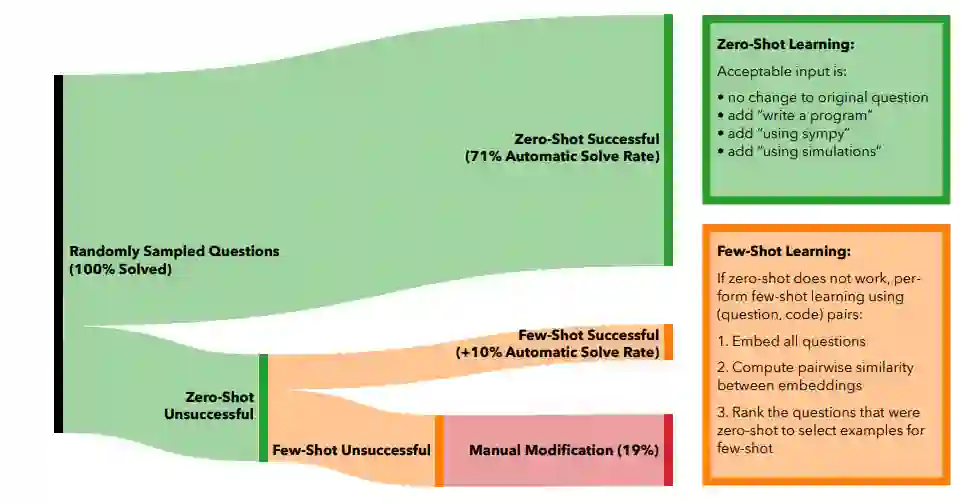
以Zero-shot learning的方式，即仅对原始问题采用自动增强的方式就可以自动解决71%的问题。

 

如果一个问题没有解决，研究人员尝试对这类问题采用Few-shot learning的方式来解决。

 

首先使用OpenAI的text-similarity-babbag-001嵌入引擎获取所有问题的2048维的embedding，然后对所有向量使用余弦相似度计算，找出与已解决的问题最相似的未解决问题。最后将最相似的问题及其相应的代码作为新问题的few-shot例子。

 

如果生成的代码没有输出正确的答案，就再增加另一个已解决的question-code对，每次都使用下一个类似的已解决的问题。

 

在实践中可以发现，使用最多5个例子进行few-shot learning的效果最好，可以自动解决的问题总数从zero-shot learning的71%增加到few-shot learning的81%

 

要想解决剩下19%的问题，就需要人工编辑的介入了。

 

研究人员首先收集所有的问题，发现这些问题大多是模糊的（vague）或包含多余的信息，如参考电影人物或当前事件等，需要对问题进行整理以提取问题的本质。

 

问题整理主要包括删除多余的信息，将长句结构分解成较小的组成部分，并将提示转换为编程格式。

 

另一种需要人工介入的情形是，一个问题的解答需要多个步骤的绘图来解释，也就是需要交互式地提示Codex，直到达到预期的可视化效果。

 

 

除了生成答案外，模型还应该能解释出答案的理由，研究人员通过提示词「Here is what the above code is doing: 1.」来引导模型生成一步步解释的结果。

 

能解答问题后，下一步就是用Codex为每门课程生成新问题。

 

研究人员创建了一个由每个班级的学生写的问题的编号列表，这个列表在随机的问题数量后被切断，其结果被用来提示Codex生成下一个问题。

 

这个过程重复进行，直到为每门课程创建了足够多的新问题。

 

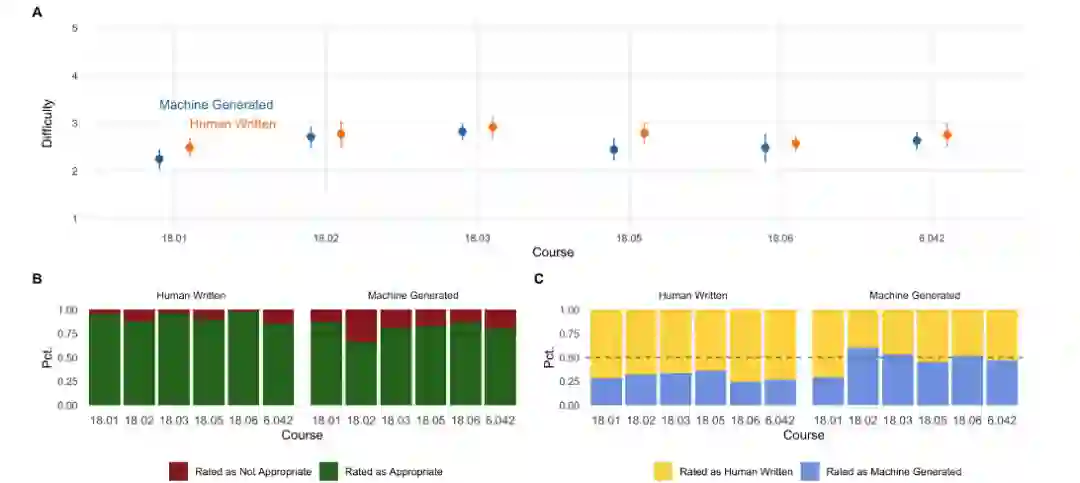
为了评估生成的问题，研究人员对参加过这些课程或其同等课程的麻省理工学院学生进行了调查，以比较机器生成的问题与课程原始的质量和难度差异。

 

 

从学生调查的结果可以看到：

 

1、机器的评分在质量上与人类出的题目已经有一战之力了；

 

2、在难度上人类的问题更适合作为课程题目，而机器生成的结果则略难一些；

 

3、超过一半的课程题目都能被学生看出来是模型生成的，最贴近人类的是18.01课程

参考资料：

https://www.reddit.com/r/artificial/comments/v8liqh/researchers_built_a_neural_network_that_not_only/