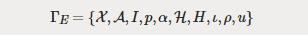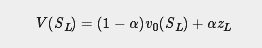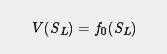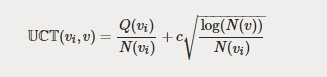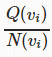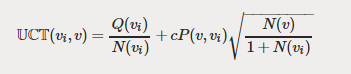AlphaGo的制胜秘诀：蒙特卡洛树搜索初学者指南

2018 年 3 月 31 日 AI100 聚焦AI的

编译 | reason_W

出品 | AI科技大本营（公众号ID：rgznai100）

长久以来，计算机在围棋领域不可能达到人类专家的水平一直是学术界的主流观点。围棋，被认为是人工智能的“圣杯”——一个我们原本希望在未来十年努力攻克的里程碑。

二十年前，“深蓝”就已经在国际象棋上超越了人类，二十年过去了，计算机却依然无法在围棋这一项目上战胜人类。围棋的运算的复杂性一度让人们将其称为“数值混沌”。甚至有人据此创作了一部科幻惊悚电影《圆周率》。

然而，出乎很多人意料的是，AlphaGo ——一个由谷歌 Deepmind 发明的围棋 AI 于 2016 年以 4:1 的成绩击败了韩国围棋冠军李世石。AlphaGo 的出现结束了围棋不可战胜的局面。一年之后，Alpha Go Zero 又以 100:0 的成绩击败了 Alpha Go Lee（击败李世石的那个）。我们不禁怀疑，人类还能追上 AI 吗？

作为人类工程学上的杰作，Alpha Go Zero 将多种方法集于一体，其核心组件包括：

蒙特卡洛树搜索 ——包含了用于树遍历的 PUCT 函数的某些变体

残差卷积网络 ——其中的策略和价值网络在游戏中被用于棋局评估以及落子位置的先验概率估计

强化学习——通过自我博弈来训练网络

在本文中，我们将就 AlphaGo 中的蒙特卡洛树搜索（MCTS/Monte Carlo Tree Search）进行专门介绍，这也是所有现代围棋程序的最核心算法。

本文内容目录如下：

1 介绍

1.1 有限双人零和回合制博弈
1.2 如何表示博弈？
1.3 如何选择最优胜率下法？极小化极大算法（Minimax）和剪枝算法（alpha-beta）

2 蒙特卡洛树搜索的基本概念

2.1 模拟

2.1.1 Alpha Go 和Alpha Zero 中的模拟

2.2 博弈树节点展开——完全展开节点和访问节点
2.3 反向传播——将模拟结果传回去
2.4 节点的统计数据
2.5 博弈树遍历
2.6 树的上限置信区间
2.6.1 Alpha Go 和Alpha Zero 中的 UCT 算法
2.6.2 Alpha Go 和Alpha Zero 的策略网络培训
2.7终止蒙特卡洛树搜索

3 总结

01 介绍

2006 年，法国的一名研究人员RémiCoulom 首次将蒙特卡洛树搜索引入到围棋程序 Crazy Stone 中，这算得上是当时计算机围棋程序的一次突破。

宏观来看，蒙特卡罗树搜索的主要目的是：给出一个博弈（即游戏）状态以选择胜率最高的下一步走法。在本文中，我们将尽量对蒙特卡罗树搜索的那些细节进行解释，方便读者了解其原理。同时，我们也会结合 Alpha Go / Zero，以解释 MCTS 变体。

▌1.1 有限双人零和回合制博弈

“博弈”——蒙特卡洛树搜索运行的框架或者说环境，其本身就是一个非常抽象的广义术语，因此本文会将讨论范围限定在一种博弈类型：有限双人零和回合制博弈 —— 乍一听这个词好像很复杂，但其实很简单，让我们把它分解成几个部分：

博弈意味着这是一个互动的情形，互动就意味着会有（一个或多个）玩家参与。

有限表示在任何时间点，玩家之间都只存在有限的互动方式。

双人有限博弈意味着博弈中只有两名玩家。

回合制，表示玩家要轮流进行行动。

最后，零和博弈——意味着博弈双方被赋予对抗性目标，换句话说：在博弈的任何终结状态中，所有玩家的收益总和等于零。有时候这样的博弈也被称为严格竞争。

这样分析下来，我们很容易就可以发现围棋、国际象棋和井字棋都是有限双人零和回合制博弈。它们都是只有两名玩家，每个人可选的执行动作有限，且该博弈是严格竞争的——两名玩家拥有对抗性目标——博弈最终收益总和为零。

注意：蒙特卡洛搜索是一个应用相当广泛的工具，不仅仅限于本文讨论的有限双人零和博弈。更为全面的概述可以参阅：http://mcts.ai/pubs/mcts-survey-master.pdf 。为了简化本教程，我们将主要讨论可能场景的某些子集。

▌1.2 如何表示博弈？

形式上，博弈由一些基本的数学实体表示。

如果不了解博弈论可以先看下这本书：

http://gametheory.tau.ac.il/arielDocs/

在一本博士水平的博弈理论书籍中，我们可以找到以下定义：

定义1. 一个广义的博弈可以由一个元组定义：

这个定义相当冗长，其中的乐趣估计也只有数学家才能体会到。

从计算机程序员的角度来看，这个正式的定义也确实可能不太容易看懂。幸运的是，我们可以用一个众所周知的数据结构来简化表示一个博弈：博弈树（move）。

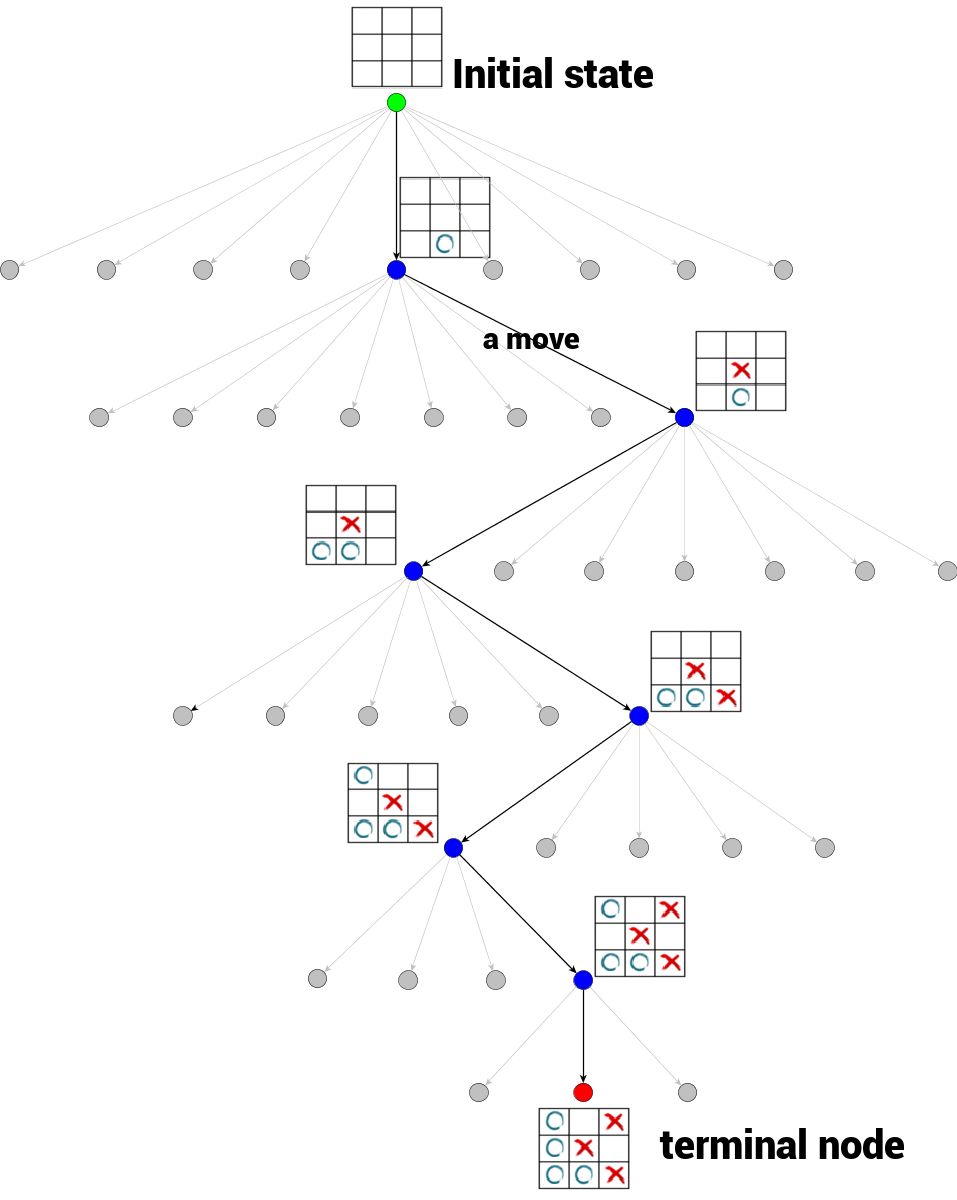
博弈树是一种树结构，其中每个节点都代表博弈的一种确定状态。从一个节点到它的一个子节点（如果存在的话）的过程被视为一个行动（move）。节点的子节点数目称为分支因子（branching factor）。树的根节点表示博弈的初始状态。我们还区分了博弈树的末端节点（terminal nodes）——没有子节点的节点，表示此处博弈无法继续进行。末端节点的状态可以被评估并用以总结博弈结果。

为限制博弈树大小，只有访问过的状态被展开，未展开的节点被标记为灰色。

在图的顶部，我们可以看到树的根节点，它代表井字棋博弈的初始状态，即空白棋盘（我们将其标记为绿色）

任何从一个节点到另一个节点的过程都是一个行动

井字棋博弈的分支因子各不相同——这取决于树的深度

博弈在末端节点结束（我们将其标记为红色）

从根节点到末端节点的树遍历代表了单次博弈的全部过程

博弈树是一种递归数据结构。每次进行最优行动并到达一个子节点后，该子节点都会被视为其子树的根节点。因此，我们可以将博弈看做一个用一系列博弈树所表示的“下一步最优行动”组成的过程序列，当然每次的根节点都是不同的。在实践中，我们不必记住到达当前状态的路径，因为那并不是当前博弈状态中的关注点。

▌1.3 如何选择最优胜率下法？极小化极大算法（Minimax）和剪枝算法（alpha-beta）

不要忘了，我们的最终目标是在给定博弈状态的情况下，利用博弈树找到最优胜率下法。但究竟如何实现呢？

这个问题没有直接的答案。首先，你不可能提前知道对手的策略——对手可能是个围棋国手，也可能只是一个刚学会围棋的菜鸟。就拿国际象棋来说，如果事先知道了对手是一个业余玩家（在数学中，这被称为已知对手的“混合策略”），我们只要选择简单的策略来欺骗他就可以迅速获胜。但很明显，当对手换成一名高手时，同样的策略就会适得其反。

在完全不了解对手的情况下，我们可以使用一种非常激进的策略——极小化极大算（Minimax）。在假设对手会做出最优决策的情况下，该策略可以最大化己方收益。在 A 和 B 之间的双人有限零和回合制博弈中（其中 A 会不断最大化他的收益，而 B 则会不断最小化 A 的收益），极小化极大算法可以用下面的递归公式来描述：

其中：

VA 和 VB 分别是玩家 A 和 B 的效用函数（效用 = 收益）

move 是一个函数，在给定当前状态和该状态的行动的情况下，它可以生成下一个博弈状态（即选择当前节点的其中一个子节点）

eval 是一个函数，用于（在末端节点处）评估最终博弈状态

s_hat 表示任意最终博弈状态（末端节点）

右下角公式中的负号表示该博弈为零和博弈。

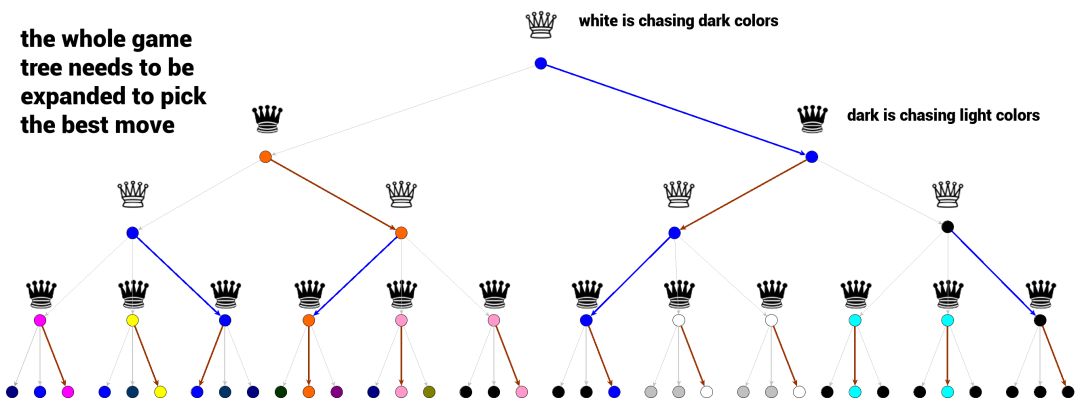
简单来说，给定状态，并假设对手试图最小化我们的收益，该算法希望找到一个可以最大化己方收益的行动。很自然这也是该算法得名极小化极大算法的原因。现在我们需要做的就是展开整个博弈树，并反向传播根据递归公式给出的规则得到的值。

上面的博弈树说明了如何在极小化极大算法中选择最优行动。白皇后要吃掉所有的黑棋，就要选择颜色尽可能深（尽可能黑）的博弈结果（奖励值 = 像素强度），而黑皇后则相反，要选择颜色最浅的路径。每一层上的每个选择都是极小化极大算法判断的最优结果。

我们可以从底部的末端节点开始看，其选择显而易见。黑皇后会颜色最浅的路径，然后白皇后为了得到最大奖励，将并选择颜色最深（最黑）的路径，依此类推......直到路径到达代表当前博弈状态的节点。这就是极小化极大算法的基本工作原理。

极小化极大算法的最大弱点是它需要展开整个博弈树。在面对分支因子高的博弈（如围棋或国际象棋）时，该算法生成的博弈树就会十分巨大，难以计算。

那么有没有补救办法呢？

一种方法是仅在特定的阈值深度 d 内展开我们的博弈树。但是，这种做法不能保证阈值深度 d 内的所有节点都是末端节点，因此我们需要一个评估非最终博弈状态的函数。这对于人类来说非常自然：即使博弈仍在继续，我们也可以通过查看国际象棋或围棋的棋盘预测赢家。比如下面这种棋局我们就可以很容易猜到结局。

另一种克服博弈树过大问题的方法是通过 alpha-beta 剪枝算法修剪博弈树。alpha-beta 剪枝算法可以看作升级版的极小化极大算法。它以极小化极大的方式遍历博弈树，同时避免某些分支的展开。其结果在最好的情况下与极小化极大算法结果相同，但优势在于 alpha-beta 剪枝算法通过减少搜索空间提高了搜索效率。

关于极小化极大算法和 alpha-beta 剪枝算法的更多介绍读者可以参考这里（https://www.youtube.com/watch?v=STjW3eH0Cik）。

总之 Minimax / Alpha-beta 剪枝算法已经是非常成熟的解决方案，现在已经被成功用在了各种的博弈引擎中，比如 Stockfish —— Alpha Zero 的主要竞争对手之一。

02 蒙特卡洛树搜索的基本概念

上面我们介绍了两种基本的搜索策略。但在蒙特卡洛树搜索算法中，最优行动却是以一种非常不同的方式计算出来的。顾名思义，蒙特卡洛树搜索会进行多次模拟博弈，并根据模拟结果尝试预测最优行动。

蒙特卡洛树搜索的主要概念是搜索。搜索是一组沿着博弈树向下的遍历过程。单次遍历的路径会从根节点（当前博弈状态）开始，一直到达未完全展开的节点。未完全展开的节点意味着其子节点至少有一个未被访问。

当遇到未完全展开的节点时，其未访问子节点中的一个会被选为单次模拟的根节点。然后模拟结果会被反向传播会当前的根节点，并更新博弈树节点的统计信息。一旦搜索（受时间或计算能力限制）终止，算法就会根据收集的统计信息选择行动策略。

还有很多地方不清楚？我们可以试着先思考一下这一过程中的几个关键问题：

什么是展开或未完全展开的博弈树节点？

在搜索过程中，“向下遍历”意味着什么？下一个（子）节点如何选择？

什么是模拟？

什么是反向传播？

什么是在展开的博弈树节点中被反向传播和更新的统计数据？

最后的行动策略如何选择？

下面，我们将一步步解决这些问题，帮助大家理解蒙特卡洛树搜索的过程。

▌2.1 模拟

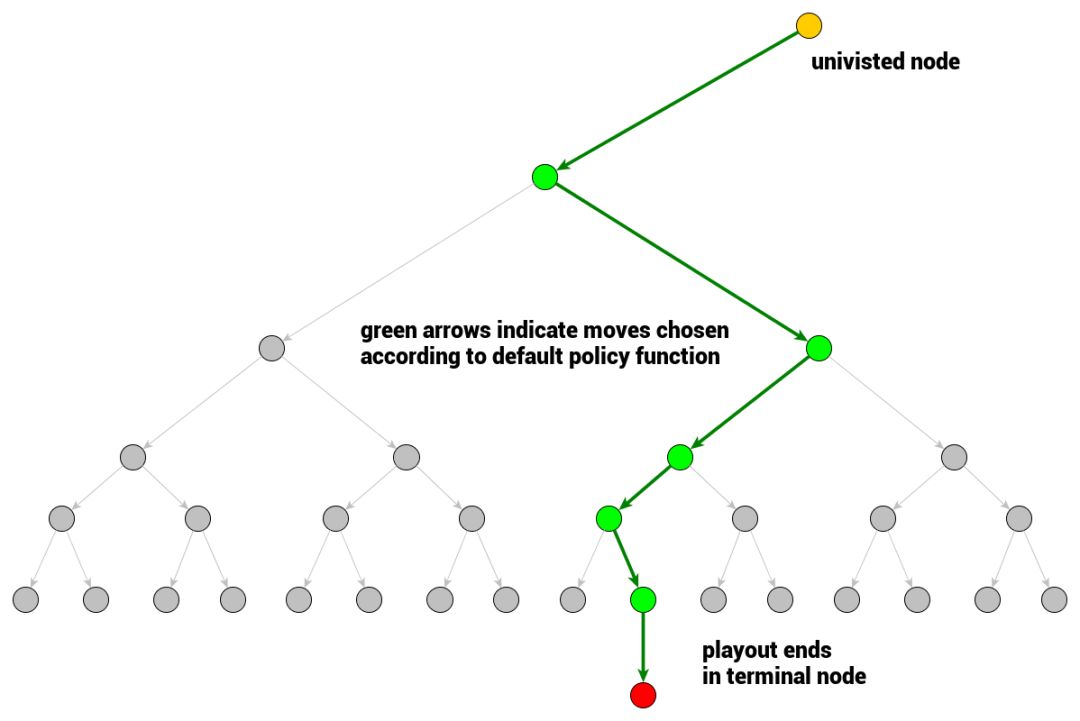
首先我们来看模拟。这一过程的解释不太依赖其他术语的定义。模拟是一种单一的博弈行为——一系列从当前节点（表示博弈状态）开始并终止于可计算博弈结果的末端节点的动作序列。模拟是对博弈树节点评估的近似计算，这一过程会从该节点处开始以某种随机博弈的方式进行。

那么，在模拟过程中我们如何选择动作呢？答案就是 rollout 策略函数：

该函数会根据输入的博弈状态产生下一个“移动/动作”。在实践中，这一函数的计算速度很快，从而可以进行很多次的模拟——默认的 rollout 策略函数会使用服从均匀分布的随机采样。

2.1.1 Alpha Go 和 Alpha Zero 中的模拟

在 Alpha Go Lee 中，叶子 S_L 的评估是以下两部分的加权和：

标准 rollout 评估 z_L ，它采用了自定义快速 rollout 策略，这是一个具有人工特征的浅层 softmax 神经网络
价值网络，它会从 Alpha Go 的自我博弈中抽取 30 万个不同的位置进行训练，通过 13 层卷积神经网络 v_0 给出位置评估

在 Alpha Zero 中， Deepmind 的工程师更进一步，他们根本不执行 playout ，而是直接用19 层 CNN 残留网络评估当前节点。在 Alpha Zero 中，他们有一个网络 f_0，可以马上输出位置评估和移动概率向量。

模拟 / rollout 的最简单形式只是一系列随机的从给定的博弈状态开始并终止的行动。模拟总会产生一个评估，就围棋而言，这个评估结果就是胜利，失败或平局，但通常模拟结果出现值都是可以的。

在蒙特卡罗树搜索模拟中，我们始终都是从先前没有被访问的节点开始。现在我们就来了解一下访问节点的含义。

▌2.2 博弈树节点展开——完全展开节点和访问节点

我们可以想一下人类是如何思考围棋或国际象棋博弈的。

给定一个根节点并加上博弈规则，博弈树的其余部分其实就已经隐含地表示出来了。我们不需要将整个树存储在内存中就可以实现对它的遍历。在初始形式中，博弈树是没有展开的。在最初的博弈状态中，我们处于博弈树的根部，其余节点都还没有被访问。一旦需要选择一个行动，我们就会想象这个行动会带来的结果（即到达哪个节点位置），并分析（评估）这个行动会到达的节点位置。而那些我们从未考虑过的博弈状态则会继续等待我们去发现。

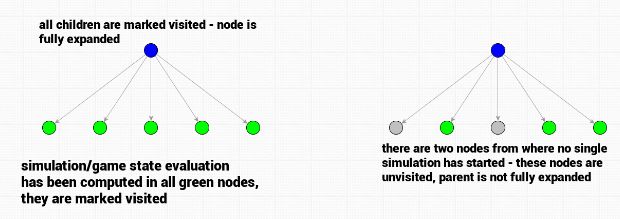
蒙特卡洛树搜索博弈树也具有同样的特性。节点会被分为已访问节点或未访问节点。那么节点被访问代表什么呢？这代表着该节点该节点已经至少进行了一次评估。如果一个节点的所有子节点都被访问了，则该节点即会认为是完全展开的，否则它就是未完全展开节点，并且有可能进一步展开。

在搜索开始时，所有根节点的子节点都是未被访问的。算法会选中一个节点，然后开始第一次模拟（评估）。

请注意，模拟期间由 rollout 策略函数选中的节点仍会被标记为未访问。即使它们通过了 rollout ，也仍然是未访问的，只有模拟开始的那个节点会被标记为已访问。

▌2.3 反向传播——将模拟结果传回去

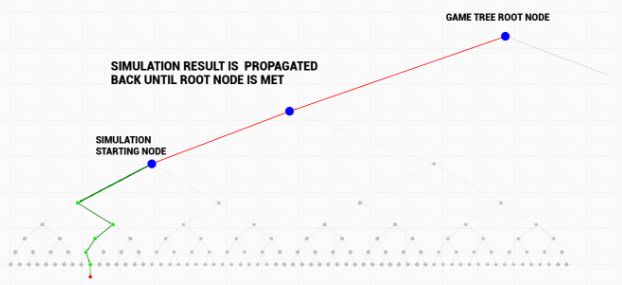
一旦完成了一次新访问节点（有时称为叶节点）的模拟，其结果就将反向传播回当前的博弈树根节点。模拟开始的节点就会被标记为已访问。

反向传播是从叶节点（模拟开始的节点）到根节点的遍历。模拟结果会被传送到根节点，并且反向传播路径上的每个节点的统计数据都会被计算/更新。反向传播了保证每个节点的统计数据将会反映在其所有后代节点所开始的模拟结果中（因为模拟结果会被传送到博弈树根节点）

▌2.4 节点的统计数据

反向传播模拟结果的目的是更新反向传播路径上的所有节点 v（包括模拟开始的节点）的总模拟奖励 Q(v) 和总访问次数 N(v) 。

Q(v) - 总模拟奖励是节点v 的一个属性，最简单的形式是通过考虑的节点的模拟结果的总和。

N(v) - 总访问次数是节点v 的另一个属性，表示一个节点在反向传播路径上的次数（同时是它对总模拟奖励贡献的次数）

每个已访问节点都会保留这两个值，一旦完成了特定次数的模拟，已访问节点就会将这些代表它们如何被展开/探索的信息存储下来。

换句话说，随便查看一个节点的统计数据，这两个值都可以反映该节点的潜在价值（总模拟奖励）以及被探索的程度（总访问次数）。总模拟奖励较高的节点会是很好的候选节点，但访问量较低的节点也可能很值得访问（因为它们还没有被很好地探索）。

现在我们已经知道了访问节点的含义，但还剩一条线没有完成。如何才能从根节点到达未访问节点，然后开始模拟呢？

▌2.5 博弈树遍历

在搜索的一开始，由于我们还没有进行过任何模拟，所以首先要选择未访问的节点。单个模拟会从这些节点开始，结果会被反向传播到根节点，然后根节点就会被认为完全展开。

但接下来我们该怎么做？如何才能从一个完全展开的节点到达未访问的节点呢？我们必须遍历已访问节点的层，但目前还没有很好的方式。

为了在路径上选择下一个节点，以通过完全展开节点 v 开始下一次模拟，我们需要考虑节点 v 本身的信息及其所有子节点 v ：v_1，v_2，…，v_k 的信息。现在让我们来看一下有哪些信息可以用吧。

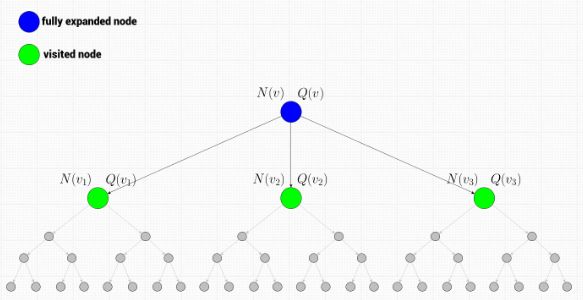
当前节点（蓝色）是完全展开的，因此它肯定已经被访问了，并且存储了节点统计信息：总模拟奖励和总访问次数。其子节点同样也是已访问的，并且存储了节点统计信息。这些值就可以用于树的上限置信区间（ UCT ）计算。

▌2.6 树的上限置信区间

UCT 函数可以让我们在访问节点中选择下一个要遍历的节点，这也是蒙特卡罗树搜索的核心函数：

可以最大化 UCT 函数值的节点就是在蒙特卡洛树搜索树遍历中要选择的节点。让我们来看看这个函数：

首先，该函数是为节点 v 的子节点 v_i 定义的，它同样是两部分的和。

第一部分是

也被称为 exploitation 分量，可以被看作是胜率——用总模拟奖励除以总访问次数，就可以得到在节点v_i中的获胜比例。这一部分看起来很靠谱——因为我们会愿意遍历具有高胜率的节点。

为什么我们不能只使用 exploitation 分量呢？因为这样算法很快就会以对那些在搜索开始就带来一个获胜模拟的节点进行贪婪探索告终。

比方说：假设我们只使用 exploitation 分量开始蒙特卡罗树搜索。从一个根节点开始，我们会为所有子节点运行一次模拟，然后下一步就会只访问那些模拟结果至少有一次胜利的节点。第一次模拟失败的节点则会被立即放弃，而没有任何改进的机会。这样是非常短视的做法，难以实现全局最优。

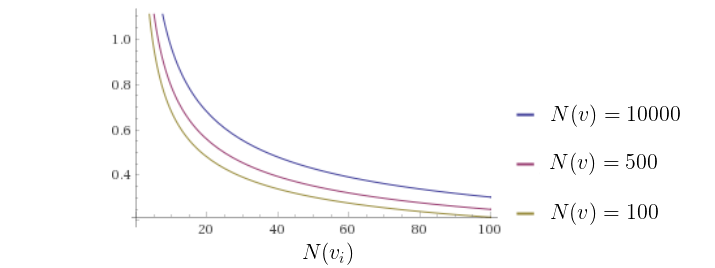
因此我们有 UCT 的第二部分，探索分量（exploration component）。探索分量偏向于那些尚未探索过的节点，即那些相对访问次数较少的节点（即 N(vi) 较低的节点）。我们来看看 UCT 函数的探索分量 ——它会随着节点访问次数的增加而减小，并且将为访问次数较少的节点提供更高的选择可能性，从而引导搜索进行探索。

UCT 公式中的参数 c 是用来在蒙特卡洛树搜索中的 expolitation 与 exploration 之间进行平衡的。

2.6.1 Alpha Go 和Alpha Zero 中的 UCT 算法

在 Alpha Go Lee 和 Alpha Zero 中，博弈树遍历是通过最大化下面这个 UCT 变体进行的：

其中 P(v_i, v) 是行动（从 v 到 v_i ）的先验概率，其值来自被称为策略网络的深度神经网络的输出。策略网络是一种函数，它会根据博弈状态产生可能移动的概率分布（请注意，这一点与快速 rollout 策略不同）。这里的目的是将搜索空间缩小到合理的移动范围内——将其添加到 exploration 分量将有助于 exploration 保持合理的移动范围。

2.6.2 Alpha Go 和 Alpha Zero 的策略网络训练

Alpha Go 有两个策略网络：

SL策略网络 ，基于人类博弈数据集以有监督的方式进行训练。
RL策略网络，增强版SL策略网络。它们有相同的架构，但RL策略网络会通过强化学习（自我博弈）进一步训练，

有趣的是，Deepmind 的蒙特卡洛树搜索变体选择了 SL 策略网络输出来进行先前的移动概率估计（P(v，v_i)），因为这一策略的实际效果更好（作者认为基于人类的数据更适合探索性移动）。那么 RL策略网络的目的是什么呢？更强大的RL策略网络被用来生成价值网络训练（用于博弈状态评估的那个）需要的 30 万个位置数据集，

而在 Alpha Zero 中，则只有一个网络 f_0 ，它既是价值网络，也是策略网络。它是完全从随机初始化开始通过自我博弈进行训练的。它会并行训练很多网络，并且在针对当前最佳神经网络进行评估后会选择最好的网络进行训练数据生成。

关于 UCT 函数的一个重要说明：在竞争博弈中，其 expolitation 分量 Q_i 的计算总是与在节点i 处移动的玩家有关。这意味着在遍历博弈树时，这个值会根据正在遍历的节点变化：对于任何两个连续的节点，这个值是相反的。

▌2.7 终止蒙特卡洛树搜索

我们现在差不多已经知道了成功实施蒙特卡罗树搜索所需的所有部分，但还有几个问题需要解决。首先，什么时候才能真正结束 MCTS ？这个答案是：看情况。在构建一个博弈引擎时，你的“思考时间”可能是有限的，再加上你的计算能力也有其限制。因此，最稳妥的选择是只要在资源允许范围内，就可以运行 MCTS 。

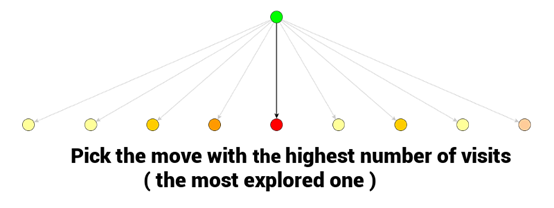
一旦完成 MCTS ，最优的一步通常是总访问次数 N(v_i) 最高的节点，因为它的值是被估计的最好的（节点的自身估计值一定是很高的，并且同是也是被探索次数最多的节点）

在使用蒙特卡洛树搜索选择了下一步之后，我们选择的节点就会成为对手下一步的博弈初始状态。一旦他走出了他那一步，我们就可以从表示对手所选择的博弈状态的节点开始，再次开始蒙特卡罗树搜索。而之前 MCTS 轮次的一些统计数据仍有可能存在于我们正在考虑的新分支中。这就可以重复使用统计数据，而不需要从头开始构建新的树——事实上，这也是 Alpha Go / Alpha Zero 的创造者做的工作。

03 总结

现在，我们终于可以把所有的东西放在一起了。回顾一下蒙特卡洛树搜索的第一个定义，我们可以用伪代码（pseudo-code）把它表示出来：

def monte_carlo_tree_search(root):
    while resources_left(time, computational power):
        leaf = traverse(root) # leaf = unvisited node 
        simulation_result = rollout(leaf)
        backpropagate(leaf, simulation_result)
    return best_child(root)
def traverse(node):
    while fully_expanded(node):
        node = best_uct(node)
    return pick_univisted(node.children) or node # in case no children are present / node is terminal 
def rollout(node):
    while non_terminal(node):
        node = rollout_policy(node)
    return result(node) 
def rollout_policy(node):
    return pick_random(node.children)
def backpropagate(node, result):
   if is_root(node) return 
   node.stats = update_stats(node, result) 
   backpropagate(node.parent)
def best_child(node):
    pick child with highest number of visits