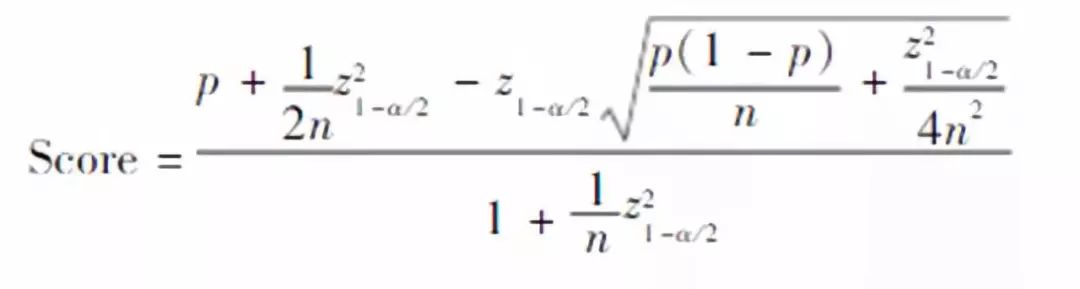基于统计思想下的推荐系统

基于统计思想下的推荐系统是什么样的？文章为你揭开迷雾。

我们先做如下设定：

每个用户的打分都是独立事件。

用户只有两个选择，要么投喜欢’1’，要么投不喜欢’0’。

如果总人数为n，其中喜欢的为k，那么喜欢的比例p就等于k/n。

这是一种统计分布，叫做”二项分布”（binomial distribution）

理论上讲，p越大应该越好，但是n的不同，导致p的可信性有差异。100个人投票，50个人投喜欢;10个人投票，6个人喜欢，我们不能说后者比前者要好。

所以这边同时要考虑（p，n）

刚才说满足二项分布，这里p可以看作”二项分布”中某个事件的发生概率，因此我们可以计算出p的置信区间。

所谓”置信区间”，就是说，以某个概率而言，p会落在的那个区间。

置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信区间给出的是被测量参数的测量值的可信程度，即前面所要求的“一个概率”，也就是结论的可信程度。

二项分布的置信区间有多种计算公式，最常见的是”正态区间”（Normal approximation interval）。但是，它只适用于样本较多的情况（np > 5 且 n（1 − p）> 5），对于小样本，它的准确性很差。

这边，我推荐用t检验来衡量小样本的数据，可以解决数据过少准确率不高的问题。

这样一来，排名算法就比较清晰了：

第一步，计算每个case的p（好评率）。

第二步，计算每个”好评率”的置信区间（参考z Test或者t Test，以95%的概率来处理）。

第三步，根据置信区间的下限值，进行排名。这个值越大，排名就越高。

解释一下，n为评价数，p为好评率，z为对应检验对应概率区间下的统计量

比如t-分布：

可以看到，当n的值足够大时，这个下限值会趋向p，如果n非常小，这个下限值会大大小于p，更加符合实际。

Reddit的评论排名，目前就使用这个算法。国内的化，滴滴也有部分业务涉及，效果也不错。

除此之外，在计算排名的时候，我们通常会考虑三个事情

上文讲到的，次数+好评率的分布，次数越多好评率越可靠，好评率越高该项越值得推荐

时间因素，如果一个项目是10天前推送的，一个项目是昨天推送的，很明显前者的次数远大于后者

影响权重，你这边只考虑了喜欢和不喜欢，其实所有的排序不可能只以1个维度考虑，通常会考虑多个维度，比如浏览次数，搜索次数等，你需要考虑每个的重要性或者说权重大小

1.这里就不讲了，其他方法也有很多，比如贝叶斯平均的优化版本、再比如经典的Hacker公式：

2.时间因素：

时间越久，代表之前的投票结果对当前的影响越小，这边有很多不同的影响方式，举几个例子：

比如艾宾浩斯遗忘规律：

这里的c、k决定下降速度，业务运用过程中，c值一般在[1,2],k值一般在[1.5,2.5]

比如时效衰减：

这里就是比较常见的移动窗口式的，永远只看近期某一段时间，而且时间内呈线性下降，不过可以改变变化方式

3.不同种的属性对于结果的影响自然不同

举个例子，用户主动搜索和用户浏览相比，用户主动搜索的情况下，用户的需求更为强烈。

通常需要判断这些强烈程度都是通过：

相关性：看因变量与自变量之间的相关系数，如：cor函数

importance：看删除或者修改自变量，对应变量的判断影响大小，如：randomForest的重要性

离散程度：看自变量的数据分布是否足够分散，是否具有判断依据，如：变异系数或者pca等等。

End.

作者：沙韬伟

来源：http://www.36dsj.com/archives/89802

识别下图二维码，加“数盟社区”为好友，回复暗号“入群”，加入数盟社区交流群，群内持续有干货分享~~

本周干货内容：内容型产品的数据驱动实践

媒体合作请联系：

邮箱：xiangxiaoqing@stormorai.com