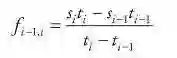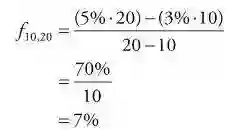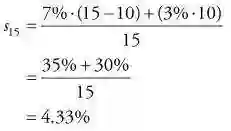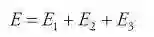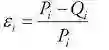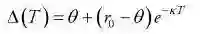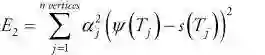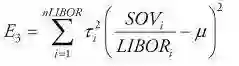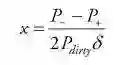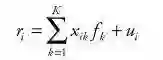Barra利率风险模型

2017 年 7 月 27 日 私募工场

私募工场（ID：Funds-Works，微信：guo5_guoguo）：两万多实名注册会员，三百多家深度尽调私募，历经两年多实盘业绩跟踪，每日净值数据分析，关键点变盘持仓数据解析，上百家精选私募证券投资机构，值得每一位高净值投资者信赖。主要为资金方提供资产配置服务，投顾筛选尽职调查服务，包括定制化私募基金产品设计、私募基金产品分析、私募投资策略分析、基金产品业绩归因、投顾业绩调查等。

私募工场：专业才是匠心

业绩鉴定：guo5_guoguo

投顾\资金：506743560@qq.com

认购咨询：15034081448

前言

准确的利率风险模型取决于利率的期限结构。期限结构是描述发行人对每个期限借入的利率今天必须支付价格。在发达市场，高评分级别或低违约风险债券的收益率与政府债券的收益率密切相关。因此，政府利率的期限结构的变化意味着这种债券的定价的变化。期限结构可以以任何数量的方式变化：所有期限的债券的收益率可以上升或下降，或者到期期限杆一端的债券收益率可以上升或下降，而另一端保持不变。以上的变化是高评分级别债券投资组合风险的主要贡献者。

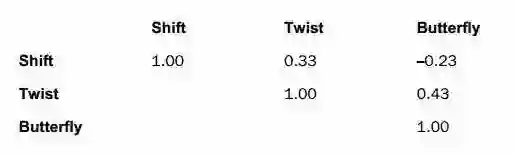
Barra的资产估值模型包含一个利率模型，从债券和其他金融工具的观察价格推断。期限结构估计算法的基本目的是找出使模型和市场价格之间的差异最小的利率。我们使用约束来平滑期限结构和LIBOR（伦敦隔夜拆借利率）驱动规格，以获得较短的利率。我们这样做是为了消除对估计期特有影响的扭曲。接下来，我们将主成分分析应用于从期限结构变化的历史数值估计的关键利率协方差矩阵。三个主要分量或具有最大方差的特征向量是移位，扭曲和蝶形因子。

由于篇幅限制，本文分为上下两篇，上篇简单介绍利率期限结构模型构建的思路与估计过程，以及详细讲解估计利率结构的目标函数的三个组成部分。下篇对因子曝露的计算以及因子相关性做了研究，并对模型的更新与改进提出了看法，最后还会对前文提到的概念加以补充解释。

（一）、估计过程概述

我们从债券超额收益对因子风险的横截面数据回归计算因子回报。主成分分析相当于“旋转”因子和协方差矩阵映射到协方差矩阵对角的表达式子中。通过保持只有前三个因子，我们保留主要风险来源，同时减少虚假相关的可能性。旋转矩阵基础的因子是正交的，是利率变化的加权组合。协方差矩阵的对角线元素是因子的样本内方差。我们用每月移动，扭曲和蝴蝶回报的时间序列生成3X3模型的利率风险矩阵。因子波动率（表示为一个标准差）和相关性确定利率矩阵。

在接下去分析之前，我们回顾一下：模型估计过程

1.数据采集

2.描述符选择和测试

3.描述符标准化

4.风险指数制定

5.行业分配

6.因子回归估计

a.一个协方差矩阵计算

b.指数加权

c.协方差矩阵缩放：DEWIV和GARCH

7.特定风险预测

a.一个平均特定风险估计

b.相对特定风险估计

c .平均和相对预测

8.模型更新

（二）、数据采集

我们获得在29个市场发行的地方政府债券，四个市场发行的通货膨胀保障债券（IPBs），美国发行的AAA级免税市政债券和23个市场的LIBOR/掉期曲线的每日价格数据。

（三）、期限结构说明

由于利率既不是买进也不是卖出，因此期限结构是派生变量。借款人的期限结构不同，并且在一天中可能发生剧烈变化。我们估计每日估值和暴露计算的期限结构。

过程：

我们通过一个数值过程来确定期限结构，在预定义的顶点设置即期汇率以最小化观察债券价格和理论债券价格之间的差异。利率期限结构由一组顶点的即期汇率指定。在短端使用更高密度的顶点以反映更大量的短期可用信息。插值用于计算顶点之间的到期率。内插规则假定前向速率在顶点之间是恒定的。我们约束优化以保持这些远期利率为正。然后，我们继续复利率。ti-1和ti之间的前向速率首先通过下式获得：

其中：

fi-1,I = 周期ti-1到ti的前进速率

si = 到期的即期汇率

ti = 到期前的时间长度

然后通过使用以下公式内插来确定顶点之间的点率：

其中：

si= 顶点i的现货率

fi = 周期ti-1到ti的前进速率

t = 到期前的时间长度

假设10年期现汇率s10为3％，20年期现汇率s20为5％。然后10到20的远期汇率是：

15年的即期汇率为：

估计算法实现：

我们使用由三个部分组成的目标函数来估计利率结构。目标函数表示为：

第一项最小化期限结构中市场价格和拟合价格之间的差异，第二项使结构受到平滑约束；第三项使用LIBOR driven规范来确定没有短期主权问题的市场的期限结构的短端顶点。目标函数中的项包含用于控制不同效应的相对影响的权重。例如，将大权重放置在第二项（E2）上将迫使得到的利率结构非常平滑。

平方相对定价错误的总和（E1）：

目标函数中的第一个和主导项是估计领域中债券的相对定价误差的平方之和。它最小化了期限结构中市场价格和拟合价格之间的差异。定价误差项E1由下式给出：

其中：

ωi= 权重

εi = 相对定价误差

相对定价误差εi由下式给出：

其中：

Pi= 债券市场价格

Qi= 债券i的贴现价格

加权方案（ωi）可以用于减少可回购债券。由于模型价格Qi取决于利率期限结构，利率期限结构的变化引起E1的变化。拟合程序通过移动速率运作，直到找到拟合价格和市场价格之间的最小差值。

（四）、平滑功能（E2）

因为在目标函数中仅由E1产生的利率结构可能由于数据中的噪声或数据与顶点的位置之间的失配而具有特性，所以包括第二项E2。

该项基于充当平滑函数的三参数方程族，函数族表示为：

其中：

θ = 长速率

r0= 短期利率

κ = 衰减常数

T = 项

参数θ，r0和κ与点价一起联合估计。

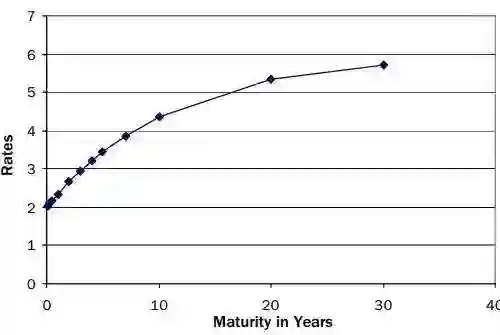
图1.典型平滑曲线

三个参数（即r0 = 2％，θ= 6％，κ= 0.09）以及顶点处的速率是拟合程序的输出。通常，所有参数为正，θ> r0。

平滑函数的离散版本产生目标函数的第二项，表示为：

其中：

αj = 平滑项的权重

ψ = 平滑曲线

Tj= 顶点j的成熟度

s(T) = 点率曲线

在上面的等式中，αj是控制不同期限的平滑项的相对重要性的权重，对于较短的期限更小，因此平滑函数对1年顶点的影响小于30年顶点的影响。

（五）、短端形状校正（E3）

用于确定期限结构的债券总体不包括在一年内有剩余到期期限的债券。这些债券往往相对缺乏流动性，因此它们的价格不反映当前的利率。因此，目标函数中通常没有足够的信息可靠地确定一年内的关键利率。这个问题可以在一些市场通过增加国库券或等价资产来处理。私募工场（ID：Funds-Works，微信：guo5_guoguo）但是，许多重要市场不包括国内短期政府问题。因此，LIBOR利率结构的形状被用作政府期限结构的短端形状的指标。由于LIBOR利率不是默认免费的，它们不直接包括在政府期限结构估计中。相反，我们假设政府和一年期LIBOR利率之间的比率对于期限结构的短期基本上是不变的。这个假设是通过对目标函数添加第三项来实现的，即：

其中：

τi = 第i个短期约束项的权重

μ = LIBOR与主权利率之间的不变比率

常数μ通常在0.7和1.05之间。与点率及平滑参数一起，通过估计方程找到μ，权重τi，可以单独校准到每个市场。E1上的权重大于E3上的权重，因此如果有短的债券，它们将用于确定期限结构的短期。例如，如果国库券信息可用，则所得到的低E1权重将在估计中去强调E3项。

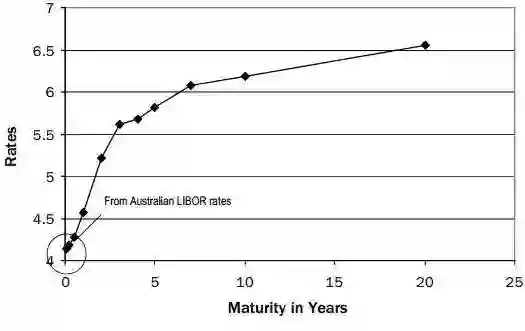
图2.估计的澳大利亚资金期限结构

在这些估计的利率中，短端的形状由LIBOR曲线给出。

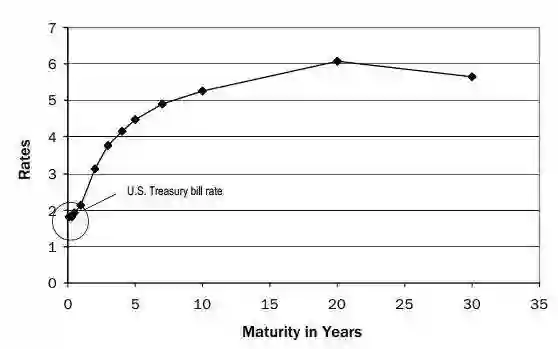
图3.估计的美国财政期限结构

因为国库券信息可用于美国市场，所以目标函数的第三项（E3）中的权重很小。

由于篇幅限制，上篇对利率期限结构模型构建的思路与估计过程的介绍就到此为止。下篇对因子曝露的计算以及因子相关性做了研究，并对模型的更新与改进提出了看法，最后还会对前文提到的概念加以补充解释。

（六）、因子形状确定

现在可以从历史利率期限结构生成点率协方差矩阵。首先为每个标准顶点创建点率的月-月差异的时间序列。从这些时间序列，我们获得密钥速率协方差矩阵。该矩阵的特征向量或主成分对应于利率结构的不相关运动。三个最大的贡献者（移位，扭曲和蝴蝶（STB））通常占经验波动率的约95％。

在具有大量债券代表广泛成熟期的市场（例如名义美国市场）中，这三个因子是显着的。在IPB市场中，较少的因子是相关的。一般来说，IPB市场由一小部分长期成熟的债券组成。简单起见，我们将这些实际市场中的移动因子视为利率期限结构的均匀、平行移动。扭曲因子（如果存在的话）是平行移动的风险残余的主要来源。

（七）、因子暴露计算

期限结构因子风险通过数值微分来计算。债券或投资组合对风险因子的暴露是其价值对因子水平变化的敏感性。例如，有效期是价值对利率平行变动的敏感性。私募工场（ID：Funds-Works，微信：guo5_guoguo）利率结构被STB因子的小标量倍数冲击或上下移动，导致债券被重估。换句话说，我们计算债券的价格如何随收益率曲线的给定变化而变化，即“向上”和“向下”值之间的差值除以移位大小的两倍。数学公式如下：

其中：

x = 因子暴露

P+、P-= 通过冲击利率结构获得的债券现值

Pdirty= 债券的脏价（指债券包括应计利息的现金流现值）

δ = 冲击大小（通常为25 bps）

（八）、估计因子回报

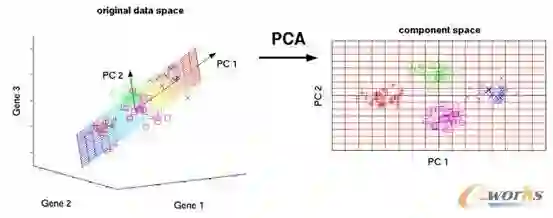
首先，我们确定解释资产回报的因子，并计算这些因子的风险敞口。然后，我们通过回归计算风险暴露与实现债券回报来估计因子回报。

其中：

rj= 超额收益向量

xi= 因子暴露矩阵

f = 因子回报的向量

ui= 具体回报的向量

回归范围包括在月初开始和结束时在既定市场指数中的债券集。

（九）、构造利率结构协方差矩阵

我们使用STB因子回报的时间序列来生成协方差矩阵。

图4.STB协方差矩阵（2000年11月30日）

对角线显示了波动率，即年回报的标准偏差。偏对角线显示因子之间的相关性。其中，STB（2000年11月30日）以每年的基点报告波动率。年化数字是从每月时间序列乘以每月估计得到的。在发达市场，典型的转移波动率为每年65-100个bps（每月约20-30个bps）。

（十）、相关协方差矩阵

原则上，可以从利率结构的变化到因子的回归来估计因子回报。这种简单的方法导致样本中的对角协方差矩阵。但它没有考虑债券沿着成熟度谱的不均匀分布。因此，我们拒绝了这种方法。私募工场（ID：Funds-Works，微信：guo5_guoguo）另一方面，基于债券收益的回归不仅考虑了不均匀分布，而且考虑了随着分布动态变化。用这种回归，风险的部分由债券特定因子占据的比例下降20％，而共同因子解释的部分相应地增加。

然而，基于债券收益的回归结果导致可以高达0.5的非平凡因子相关。用于估计因子回报的债券回归，应用于因子的初始平滑过程，以及样本外因子回报有助于增强其相关性。

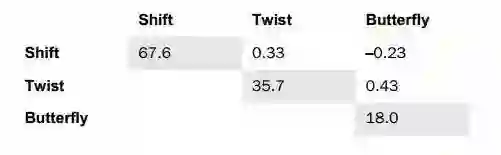
图5.英国STB之间的相关性

截至2000年11月30日的回归来自用于估计因子回报的债券回报回归，应用于因子的初始平滑过程，以及样本外回报率。这些相关性携带了对风险预测重要的信息。只要相关性不完整，模型的解释能力就不会受到影响。

对于美国城市债券市场，我们使用基于关键利率的期限-结构因子模型，从国家AAA级的一般债务债券的收益率曲线得出结论。

（十一）、更新模型

将最近的基本数据和市场数据用于计算债券风险暴露的因子和估计最近一个月的要素收益率。利率结构是每天估计的，但是风险因子的协方差是每月估计的。私募工场（ID：Funds-Works，微信：guo5_guoguo）我们对上个月的资产收益进行横截面回归。这产生了我们用于更新协方差矩阵的因子回报。STB因子的精确基础形式取决于估计期、平滑技术、体重指数，和其他细节。由于密钥速率矩阵演变缓慢，因子需要偶尔地重新估计，而不是频繁的回顾和重新估计。

附件1.关于通货膨胀保护债券

通货膨胀保障债券（IPB）是一种固定收入证券，其本金定期调整以提供固定回报率超过通货膨胀率。由发行人确定时间量，调整滞后于预先规定的通货膨胀量。息票是应用于调整后的本金的固定利率。指的是在美国财政部通货膨胀保障债券的情况下，财政部支付固定的通货膨胀率（根据所有城市消费者的非季节性调整的美国城市平均所有项目消费者价格指数或CPI）。调整滞后于CPI释放两个月，以消除下一个票面的名义金额的模糊性。对于IPB包括投资组合的显著部分的程度，准确可靠地区分实际收益率曲线的移动的风险模型（这些证券直接依赖于）与标准对称曲线的相关性。

barra风险预测

为了预测每月IPB名义回报的风险，其收益以实际或经通货膨胀调整的货币表示。IPB可以被看作是普通的固定主债券。IPB价格，在每个市场都有实际价格，但用于估计实际收益率曲线的是英国报价。然后通过应用标准主成分分析来确定真实风险因子和实际回报的风险预测，这是与名义市场使用的方法。最后，实际收益率通过rN= rR + rI近似与名义收益相关，其中rN是IPB的名义收益，rR是实际收益，rI是由于通货膨胀调整因子的收益。由于通货膨胀指数和债券的通货膨胀调整之间的滞后，rI事先已知一个月以上。因此，对于相应的风险预测，σN=σR，其中σN是名义回报风险，σR是实际回报风险。

附件2.关于美国城市债券

市政债券是国家、县、市和其他地方发行的债务，是政府实体支持政府日常需要或为公共利益进行特别项目。市场债券市场受到与应税债券市场主要驱动力不同的金融因子的影响。除了税务处理，市政债券或市政债券的明显差异外，还包括：

①大量（大约两百万）相对较小，流动性不足的问题。

②其他选项功能，例如预退款。

Barra的美国市政债券模型是基于AAA（无保险），AA，A和BBB的国家一般债务（GO）由债券的四个收益率曲线的历史数据得出的。这些收益的历史可以追溯到1994年，可以用于构建模型。风险模型结构类似于应税美国模型。与应税模型的投资级部分一样，风险的主要贡献来自于市场范围的利率水平。这些在市政债券模型中由八个关键的利率因子捕获：1，2，3，5，7，10，20和30年。而不是遵循通过“自举”这一计算即期汇率的通常做法。通过我们的标准即期汇率估计机制的修改版本，计算最小化债券全域的均方根定价误差的当前水平。这是因为到期日超过10年的市场收益率是以收益率报价的可回购债券的形式呈现的。均方根最小化方法允许我们正确处理较长期限结构收益率的可调性。如果我们进行标准自举，然后使用结果即期汇率曲线来重估可赎回债券，我们将无法重现我们开始的市场收益率。

除了不可税利率因子外，模型还包括三个信用扩散因子——AA级，A级和BBB级债券各一个，是一般债务AAA曲线上相应的点差率曲线的平均扩展。因此，市政债券风险模型总共包含11个共同因子：八个关键利率和三个评级价差。除了共同因子风险之外，市政债券模型还纳入了应税发行人信用风险模型的修改版本。发行人信用风险模型使用有关信用转移率的历史信息以及当前价差水平来预测升级或降级和违约时的风险。

附件3 .关于基准收益率曲线

利率是基于主权发行人的国内债券在全球建模的。对于欧元区，除了估计每个“传统”主权发行人的利率因子之外，我们还从以GDP计值的所有欧元政府债券的总和估算欧元主权利率结构的利率和因子系数。因为利率风险是投资级证券的日常价格变动的主要来源，所以安全价格传统上是相对于全市基准收益率曲线来引用的。直到最近，在大多数市场，这个曲线是基于政府债券的收益率，通常是本国货币中信用质量最高的发行者。

这种情况已经改变，原因有几个。首先，在欧元区，没有自然的政府债券收益率曲线。法国和德国债券通常以最低收益率交易，其他发行人的收益率相当或更高。由于缺乏明显的标准，导致LIBOR /掉期曲线作为估值基准的出现。第二，美国和其他政府债券市场经历了一些技术，供给相关的扭曲，特别是自1998年以来。这些是在俄罗斯违约和LTCM崩溃时全球质量飞行的结果，债务回购2000年和2001年初，以及不断变化的发行模式，如30年期债券发行的终止。这些市场扭曲导致美国国债市场与抵押支持证券（MBS），资产支持证券（ABS）和债券市场脱钩。在不同程度上，交易者已经转移到掉期曲线作为美国的基准。

最后，互换曲线的流动性和透明度日益增长，导致人们越来越接受这些财务利率作为更广泛债务市场的参考。然而，这种接受不是普遍的。例如，英国和日本市场主要依据政府基准进行交易。因此，Barra设计了一个混合方案，允许替代观点创造利率风险的因子结构。

附件4.期限结构估计的诊断

估计算法能识别具有大定价误差的债券并消除它们。这是通过迭代过程完成的。首先，估计包括所有债券的期限结构，丢弃具有高于阈值的定价误差的债券。然后再次进行估计。私募工场（ID：Funds-Works，微信：guo5_guoguo）重复此过程，直到没有更多具有大定价错误的债券。我们使用一组自动诊断来识别利率结构估计的潜在问题。这些测量中最简单地显示了新估计的期限结构与前一天的估计期限结构之间的偏差。调查大的每日或每月更改。

此外，还需要计算均方根定价误差。在美国财政期限结构估计中，例如，存在大约110个债券，并且均方根误差范围在30至50个基点之间。虽然数字本身没有确定的解释，其值的突然变化对于标记估计中的问题是有用的。

附件5.归一化利率结构因子

密钥速率协方差矩阵的主成分分析产生STB因子，确定在关键期限的因子的相对权重。不确定因子的绝对大小。如果一个因子由常数c定标，则投资组合对该因子的暴露也由c来定标。系数的返回值按1 / c进行缩放，以便缩放比例因子抵消风险计算。移动因子大致是利率的平行变化。因此，对于不可赎回债券，转移的敞口应是与有效期相当的数字。移位曝光的幅度可以通过改变移位因子的大小来控制。按照惯例，因子被归一化，使得它们的均方值是顶点的数量（真实的平行移动在常数1被归一化），并且使得它们在长期到期时是正的。基准偏移被归一化，使得偏移曝光与可用的持续时间相当。基本扭曲和蝶形因子被归一化为具有与移位相同的幅度。这种归一化在STB因子的变换中不被保留。然而，由于变换的幅度相对较小，修正的移位曝光仍然相当于有效期。

来源：私募云通

·END·

私募工场

扫码立即关注私募工场