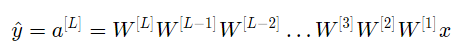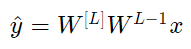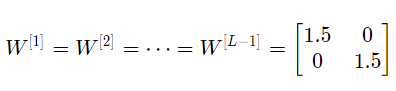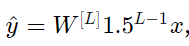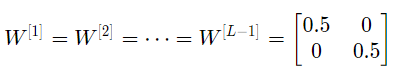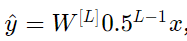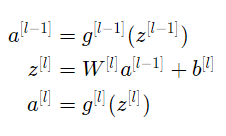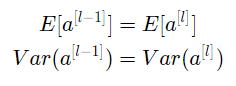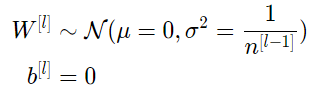一文读懂神经网络初始化！吴恩达Deeplearning.ai最新干货

来源：新智元

本文约3000字，建议阅读5分钟。

本文是deeplearning.ai的一篇技术博客，对初始化值的大小选取不当，可能造成梯度爆炸或梯度消失等问题，并提出了针对性的解决方法。

神经网络的初始化是训练流程的重要基础环节，会对模型的性能、收敛性、收敛速度等产生重要的影响。本文是deeplearning.ai的一篇技术博客，文章指出，对初始化值的大小选取不当，  可能造成梯度爆炸或梯度消失等问题，并提出了针对性的解决方法。

初始化会对深度神经网络模型的训练时间和收敛性产生重大影响。简单的初始化方法可以加速训练，但使用这些方法需要注意小心常见的陷阱。本文将解释如何有效地对神经网络参数进行初始化。

有效的初始化对构建模型至关重要

要构建机器学习算法，通常要定义一个体系结构（例如逻辑回归，支持向量机，神经网络）并对其进行训练来学习参数。下面是训练神经网络的一些常见流程：

 

初始化参数

选择优化算法

然后重复以下步骤：

1、向前传播输入

2、计算成本函数

3、使用反向传播计算与参数相关的成本梯度

4、根据优化算法，利用梯度更新每个参数

然后，给定一个新的数据点，使用模型来预测其类型。

初始化值太大\太小会导致梯度爆炸或梯度消失

初始化这一步对于模型的最终性能至关重要，需要采用正确的方法。比如对于下面的三层神经网络。可以尝试使用不同的方法初始化此网络，并观察对学习的影响。

在优化循环的每次迭代（前向，成本，后向，更新）中，我们观察到当从输出层向输入层移动时，反向传播的梯度要么被放大，要么被最小化。

假设所有激活函数都是线性的（恒等函数）。 则输出激活为：

其中 L=10 ，且W[1]、W[2]…W[L-1]都是2*2矩阵，因为从第1层到L-1层都是2个神经元，接收2个输入。为了方便分析，如果假设W[1]=W[2]=…=W[L-1]=W，那么输出预测为

如果初始化值太大或太小会造成什么结果？

情况1：初始化值过大会导致梯度爆炸

如果每个权重的初始化值都比单位矩阵稍大，即：

可简化表示为

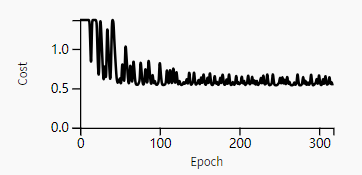
且a[l]的值随l值呈指数级增长。当这些激活用于向后传播时，会导致梯度爆炸。也就是说，与参数相关的成本梯度太大。 这导致成本围绕其最小值振荡。

初始化值太大导致成本围绕其最小值震荡

情况2：初始化值过小会导致梯度消失

类似地，如果每个权重的初始化值都比单位矩阵稍小，即：

可简化表示为

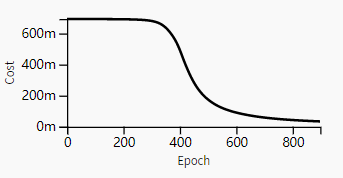
且a[l]的值随l值减少呈指数级下降。当这些激活用于后向传播时，可能会导致梯度消失。也就是说，与参数相关的成本梯度太小。这会导致成本在达到最小值之前收敛。

初始化值太小导致模型过早收敛

总而言之，使用大小不合适的值对权重进行将导致神经网络的发散或训练速度下降。 虽然我们用的是简单的对称权重矩阵来说明梯度爆炸/消失的问题，但这一现象可以推广到任何不合适的初始化值。

如何确定合适的初始化值

为了防止以上问题的出现，我们可以坚持以下经验原则：

1.激活的平均值应为零。

2.激活的方差应该在每一层保持不变。

在这两个假设下，反向传播的梯度信号不应该在任何层中乘以太小或太大的值。梯度应该可以移动到输入层，而不会爆炸或消失。

更具体地说，对于层l，其前向传播是：

我们想让下式成立:

确保均值为零，并保持每层输入方差值不变，可以保证信号不会爆炸或消失。该方法既适用于前向传播（用于激活），也适用于向后传播（用于关于激活的成本梯度）。

这里建议使用Xavier初始化（或其派生初始化方法），对于每个层l，有：

层l中的所有权重均自正态分布中随机挑选，其中均值 μ=0 ，方差E= 1/( n[l−1])，其中n[l−1] 是第l-1层网络中的神经元数量，偏差已初始化为零。

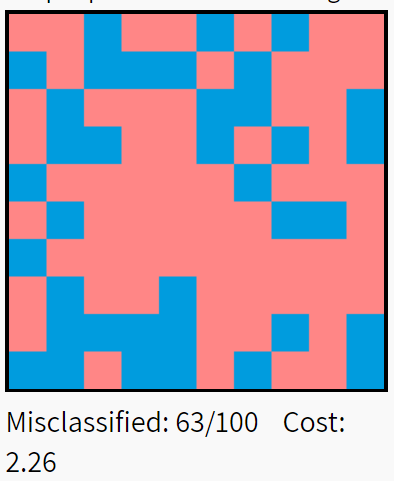
下图说明了Xavier初始化对五层全连接神经网络的影响。数据集为MNIST中选取的10000个手写数字，分类结果的红色方框表示错误分类，蓝色表示正确分类。

结果显示，Xavier初始化的模型性能显著高于uniform和标准正态分布（从上至下分别为uniform、标准正态分布、Xavier）。

结论

在实践中，使用Xavier初始化的机器学习工程师会将权重初始化为N（0，1/( n[l−1])）或N（0，2/（n[l-1]+n[1]））,其中后一个分布的方差是n[l-1]和n[1]的调和平均。

Xavier初始化可以与tanh激活一起使用。此外，还有大量其他初始化方法。 例如，如果你正在使用ReLU，则通常的初始化是He初始化，其初始化权重通过乘以Xavier初始化的方差2来初始化。 虽然这种初始化证明稍微复杂一些，但其思路与tanh是相同的。

参考链接：

https://www.deeplearning.ai/ai-notes/initialization/

编辑：王菁

校对：王欣