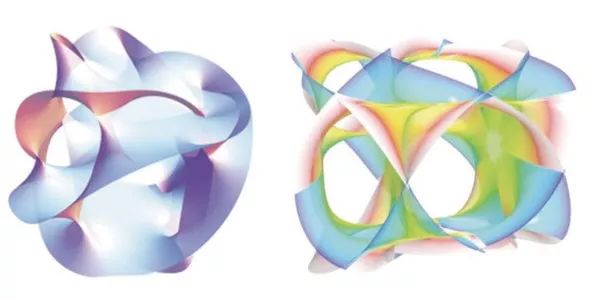丘成桐:我们真的活在十维时空吗?
作者简介: 丘成桐为美国哈佛大学数学与物理教授,美国科学院院士,中国科学院外籍院士,菲尔兹奖、克拉福德奖、沃尔夫奖得主。发展了强有力的偏微分方程技巧,使得微分几何学产生了深刻的变革,解决了卡拉比(Calabi)猜想、正质量猜想等众多难题,影响遍及理论物理和几乎所有核心数学分支。筹资成立浙江大学数学科学研究中心、香港中文大学数学研究所、北京晨兴数学中心和清华大学丘成桐数学科学中心等学术机构,并担任主任;1998 年创立世界华人数学家大会(ICCM),毎三年举办一次。由于对中国数学发展的突出贡献,获得 2003 年度中华人民共和国科学技术合作奖。科普著作有《大宇之形》(2012)、《从万里长城到巨型对撞机》(2016)、《简史:哈佛数学150年》(即将出版),主编科普杂志《数理人文》和丛书《数学与人文》。
译者简介:夏木青为香港专业数学科普译者。
本文翻译并整理自丘成桐推广《大宇之形》之各场英文演讲稿,刊登于《数理人文》杂志第2期(2014/6/15),欢迎读者朋友分享、评论和反馈建议。媒体或机构如需转载,请联系波士顿国际出版社或《数理人文》。
重点摘要
● 丘成桐因证明卡拉比猜想获得菲尔兹奖。由此确立的卡拉比-丘空间,在爱因斯坦的广义相对论里,相当于竟然存在重力非零的真空宇宙!
● 弦论是统一四种作用力最成熟的物理理论,它断言宇宙是十维的时空,除了日常的四维时空,另外卷缩的六维微小空间正是卡拉比-丘空间。
● 弦论高度整合物理和数学的深刻洞识,反过来促进了数学的新进展,镜对称预言了数学家无法想像的公式,震惊数学界。
今天要讲的,是数学和物理如何互动互利,这种关系在卡拉比-丘空间(Calabi-Yau space)和弦论的研究中尤为突出。这个题目非出偶然,它正是我和纳迪斯(Steve Nadis)的新书《大宇之形》的主旨。书中描述了这些空间背后的故事,个人的经历和几何的历史。
我写这本书,是希望读者透过它,了解数学家是如何看这世界的。数学并非一门不食人间烟火的抽象学问,相反地,它是我们认识物理世界不可或缺的工具。现在,就让我们沿着时间,或更确切地,沿着时空从头说起。
站在巨人的肩上——黎曼几何学
1969 年,我到了美国加州大学柏克莱分校念研究所。在那里我了解到,19 世纪几何学在高斯和黎曼的手上经历了一场翻天覆地的变化。黎曼的创见,颠覆了前人对空间的看法,给数学开辟了崭新的途径。
几何的对象,从此不再局限于平坦而线性的欧几里得空间内的物体。黎曼引进了更抽象的、具有任何维数的空间。在这些空间了,距离和曲率都具意义。此外,在它们上面还可以建立一套适用的微积分,作为研究与分析的工具。
大约五十年后,爱因斯坦发觉包含弯曲空间的这种几何学,刚好可用来统一牛顿的重力理论和狭义相对论,沿着新路迈进,他终于完成了著名的广义相对论。在研究所的第一年,我念了黎曼几何学。它与我在香港时学的古典几何不一样,过去我们只会讨论在线性空间里的曲线和曲面。在柏克莱,我修了史帕尼尔(Edwin Spanier)的代数拓朴、劳森(Blaine Lawson)的黎曼几何、莫瑞(Charles Morrey)的偏微分方程。此外,我还旁听了包括广义相对论在内的几门课,我如饥似渴地尽力去吸收知识。
当时柏克莱数学系大约有 500 名研究生,地狭人众,大家都没有研究室。课余的时间我都呆在数学图书馆,它简直成了我的辨公室。我孜孜不倦地找寻有兴趣的材料来看。圣诞节到了,别人都回去和家人团聚。我却在读《微分几何期刊》(Journal of Differential Geometry)上米尔诺(John Milnor)的一篇论文 , 它阐述了空间里曲率与基本群(fundamental group)的关系。我既惊且喜,因为它用到了我刚刚学过的东西。
米尔诺的文笔是如此流畅,我通读此文毫不费力。他文中提及普莱斯曼(Alexandre Preissman)的另一论文,我也极感兴趣。从这些文章中可以见到,负曲率空间的基本群受到曲率强烈的约束,必须具备某些特定的性质。
基本群是拓朴上的概念,基本上考虑的是从定点出发的所有回圈,并将可互相形变的回圈视为等价。普莱斯曼定理说,负曲率流形的基本群中,任两个可交换的元素,皆能写成某元素的自乘。这个结果很引人入胜,我试着推广普莱斯曼的结果,想看看如果空间曲率非正,结果又是如何?这是我平生第一次将空间的曲率(精确的几何描述)和比较粗糙、只留意形态特征的数学理论(称为拓朴学)联系起来。
图中每一列的形体,在拓朴学中都被视为相同,虽然几何性质显然不同。第一列是 2 维的球面;第二列是 2 维的环面。
虽然,拓朴也是一种研究空间的学问,但它不涉及距离。从这角度来看,拓朴所描绘的空间并没有几何所描绘的那样精细。几何要量度两点间的距离,对空间的属性要知道更多。这些属性可以由每一点的曲率表达出来,这便是几何了。
举例而言,甜甜圈和咖啡杯具有截然不同的几何,但它们的拓朴却无二样。同样,球面和椭球面的几何迥异但拓朴相同。作为拓朴空间,球面的基本群是无聊的,在它上面的任何闭曲线,都可以透过连续的变动而缩成一点。但环面(torus)则否,在它上面可以找到某些闭曲线,无论如何连续地变动都不会缩成一点。由此可见,球面和环面具有不同的拓朴。
球面上所有的回圈都可以缩到一个点,但环面上有些回圈,却没有这样的性质。这表示球面和环面的拓朴不一样。
普莱斯曼定理讨论了几何(曲率)如何影响拓朴(基本群),我做了点推广。在影印这些札记时,一位数学物理的博士后费雪(Arthur Fisher)嚷着要知道我干了什么。他看了那些札记后,说任何把曲率与拓朴扯上关系的结果,都会在物理学中用上。这句话在我心中留下烙印,至今不忘。
弯曲就是重力——广义相对论
狭义相对论告诉我们,时间和空间浑为一体,形成时空,不可分割。爱因斯坦进一步探究重力的本质,他的友人格罗斯曼(Marcel Grossmann)是数学家,爱氏透过他认识到黎曼和黎奇(Ricci)的工作。黎曼引进了抽象空间的概念,并且讨论了其上的距离和曲率。爱因斯坦利用这种空间,作为他研究重力的舞台。
爱因斯坦也引用了黎奇的工作,以他创造的曲率来描述物质在时空的分布。黎奇曲率乃是曲率张量的迹(trace),是曲率的某种平均值。它满足的毕安奇恒等式(Bianchi identity),奇妙地可以看成一条守恒律。爱因斯坦利用了这条守恒律来把重力几何化,从此我们不再视重力为物体之间的吸引力。新的观点是物体的存在使空间产生了曲率,重力应当看作是这种曲率的表现。
对历史有兴趣的读者,爱因斯坦的自家说辞更具说服力。他说:
这套理论指出重力场由物质的分布决定,并随之而演化,正如黎曼所猜测的那样,空间并不是绝对的,它的结构与物理不能分割。我们宇宙的几何绝不像欧氏几何那样孤立自足。
当然,爱因斯坦建立这个理论的过程绝非坦途。一开始,他想将重力理论和狭义相对论结合却遭遇失败。后来,他意识到这是非线性理论,并以重力定律在所有坐标系皆相同的等效原理(equivalence principle)作为指导原则。1912 年,他领略到必须以带劳仑兹符征(Lorentzian signature)的黎曼度量来作为重力势。另外,它还必须解决两个问题,首先是如何将狭义相对论的场方程转换到有黎曼度量的情况,然后还需要厘清决定黎曼度量的法则。1912 年到 1914 年之间,他和格罗斯曼合作,发现第一个问题要使用黎曼几何上的黎奇与李维奇威塔(LeviCivita)所发展的微分计算法,第二个问题的解答,则要应用黎曼建立的二阶微分不变量。
球面上的“直线” 就是大圆,经线都是大圆,但纬线除了赤道之外都不是大圆。想像有两个人如图从赤道开始往北方走,明明是“平行”开始的,却不自觉愈走愈近,好像有力在牵引着彼此。究其原因在于球面的曲率是正的,不像平面的曲率等于零。这说明曲率为何可解释为力。
爱因斯坦一直奋斗到 1915 年才找到正确的数学形式,建立了广义相对论,并找到能测试这个理论的天文实验方法。大概在同时,知名数学家希尔伯特(David Hilbert)也独立找到场方程的正确形式,但他没能更近一步和实验结合。
讲到自己的成就时,爱因斯坦写道:
就学问本身而言,这些理论的推导是如此行云流水,一气呵成,聪明的人花点力气就能掌握它。然而,多年来的探索,苦心孤诣,时而得意,时而气馁,到事竟成,其中甘苦,实在不足为外人道。
爱因斯坦研究重力的经历,固然令人神往,他的创获更是惊天动地。但是黎曼几何学在其中发挥的根本作用,也是昭昭然不可抹杀的。
半个多世纪后,我研习爱因斯坦方程组时,发现物质只能决定时空的部分曲率,为此心生困惑,自问能否找到一个真空,即没有物质的时空,但其曲率并不平凡,即其重力非零。当然,著名爱因斯坦方程的史瓦兹柴德(Schwarzschild)解具有这些性质。它描述的乃是非旋转的黑洞,这是个真空,但奇怪地,极端的重力产生了质量。然而这个解具有一个奇点(singularity),在那里所有物理的定律都不适用。
我要找的时空不似史瓦兹柴德解所描绘的那样是开放无垠的,反之,它是光滑不带奇点,并且是紧致(compact)而封闭的。即是说,有没有一个紧致而不含物质的空间,即封闭的真空宇宙,但其上的重力却不等于零?这问题在我心中挥之不去,我认为这种空间并不存在。如果能从数学上加以论证,这会是几何学上的一条美妙的定理。
柳暗花明又一村——卡拉比猜想
从上世纪 70 年代开始,我便在考虑这个问题。当时,我并不知道几何学家卡拉比(Eugenio Calabi)早已提出差不多同样的问题。他的提问透过颇为复杂的数学语言来表述,其中牵涉及凯勒流形(Kähler manifold)、黎奇曲率、陈氏类(Chern class)等等,看起来跟物理沾不上边。但事实上,卡拉比抽象的猜想也可以翻过来,变为广义相对论里的一个问题。
卡拉比和丘成桐摄于哈佛科学中心。
新的内容乃是要求要找的时空具有某种内在的对称性,这种对称物理学家称之为超对称(supersymmetry,用数学语言来说,在这个情况指的就是凯勒流形)。于是上述的问题便变成这样:能否找到一个紧致而不带物质的超对称空间,其中的曲率非零(即具有重力)?
卡拉比猜想不仅指出封闭而具重力的真空的存在性,而且还给出系统地大量构造这类空间的途径,大家都认为世间那有这样便宜的东西可捡。可是,纵然不乏怀疑卡拉比猜想的理由,但没人能够反证它。我与其他人一起试图证明卡拉比猜想所描述的空间并不存在,花了差不多三年。
1973 年我出席了在斯坦福大学举行的国际几何会议。这会议是由奥瑟曼(Robert Osserman)和陈省身老师组织的。也许是由于我与两人的关系,我有幸作出两次演讲。在会议期间,我告诉了一些相识的朋友,说已经找到了卡拉比猜想的反例。消息一下子传开了,徇众要求,当天晚上另作报告。那晚 30 多位几何工作者聚集在数学大楼的三楼,其中包括卡拉比、陈师和其他知名学者。我把如何构造反例说了一遍,大家似乎都非常满意。
陈省身和丘成桐。1992 年摄于台湾中央研究院。
卡拉比还为我的构造给出一个解释。大会闭幕时,陈师说我这个反例或可视为整个大会最好的成果,我听后既感意外,又兴奋不已。
可是,真理总是现实的。两个月后我收到卡拉比的信,希望我厘清反例中一些他搞不清楚的细节。看见他的信,我马上就知道我犯了错。接着的两个礼拜,我不眠不休,希望重新构造反例,身心差不多要垮掉。每次以为找到一个反例,瞬即有微妙的理由把它打掉。
经过多次失败后,我转而相信这猜想是对的。于是我便改变了方向,把全副精力放在猜想的证明上。花了几年工夫,终于在 1976 年证明了这个重要的猜想。好消息是,证明卡拉比猜想,也让我之前构造的许多“反例”变成重要的定理。
另外,在斯坦福那个会议上,物理学家葛洛克(Robert Geroch)在报告中谈到广义相对论中的一个重要课题——正质量猜想(positive mass conjecture)。这猜想指出,在任何封闭的物理系统中,总质量(能量)必须是正数。我和孙理察(Richard Schoen)埋头苦干,利用了最小曲面(minimal surface),证明了正质量猜想。
这段日子的工作把我引到广义相对论,我们证明了几条有关黑洞的定理。与相对论学者交流的愉快经验,使我更能开放怀抱与物理学家合作。几年之后,更参与了弦论的发展。
在证明卡拉比猜想时,我引进了一个方案,用以寻找满足卡拉比方程的空间,这些空间现在通称为卡拉比-丘空间。我深深地感到,我无心插柳,已经进入了一界数学高地。它必定与物理有关,并能揭开自然界深深埋藏的隐祕。然而,我并不知道这些想法在那里会大派用场,事实上,当时我懂得的物理也不多。
抚弦轻拨十维琴——弦论
1984 年,我接到物理学家赫罗维兹(Gary Horowitz)和史聪闵格(Andy Strominger)的电话。他们兴冲冲的谈到有关宇宙真空状态的一个模型,这模型是建基于一套叫弦论的崭新理论。
弦论的基本假设是,所有最基本的粒子都是由不断振动的弦线所组成的,这些弦线非常非常细小。某些弦论要跟量子力学相容不排斥,时空必须容许某种超对称性,同时时空还必须是十维的。
我在解决卡拉比猜想时证明存在的空间,得到赫罗维兹和史聪闵格的喜爱。他们相信这些空间会在弦论中担当重要的角色,原因是它们具有弦论所需的那种超对称性。他们希望知道这种看法对不对,我告诉他们,那是对的,他们听到后十分高兴。
不久,威腾(Edward Witten)打电话给我,我们是上一年在普林斯顿相识的。他认为就像当年量子力学刚刚面世那样,理论物理学最激动人心的时刻来临了。他说每一位对早期量子力学有贡献的人,都在物理学史上留名。爱因斯坦在他的后半生花了三十年致力于统一理论,但至死也未竟全功。早期弦学家如葛林(Michael Green)和史瓦兹(John Schwarz)等人的重要发现,有可能终究把所有自然力统一起来。
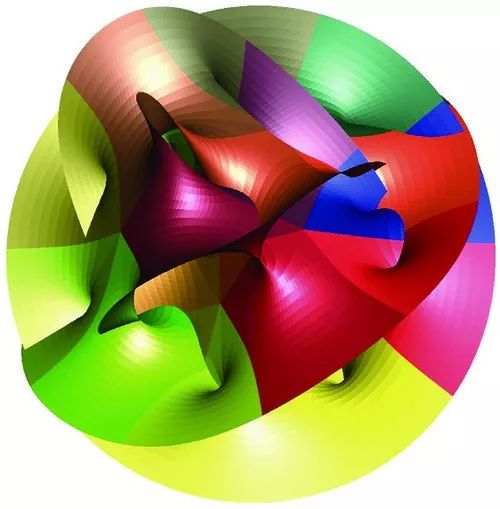
六维卡拉比-丘空间的二维“切片”。印第安那大学 Andrew J. Hanson 提供。
当时威腾正与坎德拉斯(Philip Candelas)、赫罗维兹和史聪闵格一起,希望搞清楚弦论中那多出来的六维空间的几何形状。他们认为这六维卷缩成极小的空间,并称此空间为卡拉比-丘空间,因为它源于卡拉比的猜想,并由我证明其存在。
弦论认为时空的总维数为十。我们熟悉的空间是三维,加上时间,那便是爱因斯坦理论中的四维时空。此外的六维属于卡拉比-丘空间,它独立的暗藏于四维时空的每一点里。我们看不见它,但弦论说它是存在的。
这个添了六个维度的空间够神奇了,但弦论并不止于此,它进一步指出卡拉比-丘空间的几何,决定了这个宇宙的性质和物理定律。哪种粒子能够存在,质量是多少,它们如何相互作用,甚至自然界的一些常数,都取决于卡拉比-丘空间或本书所谓“内空间”的形状。
理论物理学家利用狄拉克算子(Dirac operator)来研究粒子的属性。透过分析这个算子的谱(spectrum),可以估计能看到粒子的种类。十个维数的时空可以想成是四维时空和六维卡拉比-丘空间的乘积。因此,当我们运用分离变数法求解算子谱时,它肯定会受卡拉比-丘空间所左右。卡拉比-丘空间的直径非常小,因此非零谱所对应的粒子质量变得异常大。这类粒子很难观测到,因为它们只会在极度高能量的状态下才会出现。
另一方面,具有零谱的粒子是可能观测到的,它们取决于卡拉比-丘空间的拓朴。由此可见,这细小的六维空间,其拓朴在物理中是如何举足轻重。爱因斯坦过去指出,重力不过是时空几何的反映。弦学家更进一步,大胆地说这个宇宙的规律,都可以由卡拉比-丘空间的几何推演出来。这个六维空间究竟具有怎样的形状,显然就很重要了。弦学家正就此问题废寝忘餐,竭尽心力地研究。
威腾很想多知道一点卡拉比-丘空间。他从普林斯顿飞来圣地亚哥,与我讨论如何构造这些空间。他还希望知道究竟有多少个卡拉比-丘空间可供物理学家拣选。原先,他们认为只有少数几个拓朴类可作考虑,是以决定宇宙“内空间”的任务不难完成。可是,我们不久便发现,卡拉比-丘空间比原来估计的来得多。1980 年初,我想它只有数万个,然而,其后这数目不断增加,迄今未止。于是,决定内空间的任务一下子变得无比困难,假如稍后发现有无数卡拉比-丘空间的话,就更遥不可及了。当然,后者是真是假还有待验证,我一直相信,任何维度卡拉比-丘空间的拓朴类型都是有限的。
把四维的时空简化成无穷延伸的直线,虽然数学的直线没有厚度,但弦论说如果用威力强大的放大镜来看时空,就会发现它其实有一个隐微的厚度,任意切开,截面都是六维的卡拉比-丘空间。
于无声处听惊雷——镜对称
卡拉比-丘空间的热潮,始于 1984 年,当时的物理学家,开始了解到这些复空间或会用于新兴的理论上。热情持续了几年,便开始减退了。可是到了上世纪 80 年代末期,格林恩(Brian Greene)、普列瑟(Ronen Plesser)、坎德拉斯等人开始研究镜对称(mirror symmetry)时,卡拉比-丘空间又重新成为人们的焦点。
镜对称乃是两个具有不同拓朴的卡拉比-丘空间,看起来没有什么共通点,但却拥有相同的物理定律。具有这样关系的两个卡拉比-丘空间称为“镜伴”(mirror partner)。
1995 年,史聪闵格、札斯洛(Eric Zaslow)和我提出一个猜想,对卡拉比-丘空间的子结构提供洞识,为镜对称给出解释。根据这个 SYZ 猜想的理论,六维卡拉比-丘空间本质上可以分成两个三维空间,其中之一是三维环面。如果模仿把半径 r 变成 1/r 的操作,把这些三维环面“翻转”,并与另一个三维空间结合起来,就会得到原卡拉比-丘空间的镜伴。这个猜想提供了镜对称的几何图象,尽管目前只在一些特殊情况下被证明成立。
数学家把物理学家发现的镜关系搬过来,成为数学上强而有力的工具。在某个卡拉比-丘空间上要解决的难题,可以放到它的镜伴上去考虑,这种做法往往奏效。例如有一个求解曲线数目的问题,悬空了差不多一个世纪,就是这样破解的。它使枚举几何学(enumerative geometry)这一数学分支,重新焕发了青春。这些进展令数学家对物理学家及弦论刮目相看。
镜对称是对偶性的一个重要例子。它就像一面窗,让我们窥见卡拉比-丘空间的隐祕。利用它,我们确定了在五次三维形(一种卡拉比-丘空间)上给定阶数的有理曲线的总数,这是一个非常困难的问题。
这类问题称为舒伯特问题。它源于 19 世纪,德国数学家舒伯特(Hermann Schubert)首先证明,在五次三维形上共有 2,875 条一阶有理曲线。到了 1986 年,卡兹(Sheldon Katz)证明了有 609,250 条二阶曲线。1989 年前后,两位挪威数学家艾林斯路得(Geir Ellingsrud)和司聪默(Stein Strømme)利用代数几何的技巧,一下子找到了 2,682,549,425 条三阶曲线。
可是另一方面,以坎德拉斯为首的一组物理学家,却利用弦论找到 317,206,375 条三阶曲线。他们在寻找的过程中,用了一条并非由数学推导出来却适用于任意阶数曲线的公式。这公式的真确与否,还有待数学家验证。
1990 年 1 月,在辛格(Isadore Singer)的敦促下,我组织了弦学家和数学家首次的主要会议。大会在柏克莱的数理科学研究院(MSRI)举行。会议上拥艾林斯路得-司聪默结果的人和拥坎德拉斯团队的人分成两派,壁垒分明,各不相让。这局面维持了几个月,直到数学家在他们写的程式中发现错误,经修正后,结果竟与物理学家找到的数目完全吻合。经此一役,数学家对弦学家深刻的洞察力,不由得肃然起敬。
物理学家发现两个卡拉比-丘空间,虽然拓朴很不同,却可能对应到同一物理理论。这个性质称为镜对称,彼此对称的双方称为镜伴。
这一幕还说明了镜对称自有其深厚的数学基础。人们花了好几年,到了 1990 年代中后期,镜对称的严格数学证明,包括坎德拉斯等人的公式,才由吉文塔(Alexander Givental)以及连文豪-刘克锋-丘成桐各自独立完成。
不知有吾身 此乐最为甚
话说回来,我们必须紧记,弦“论”毕竟是一套理论而已,它还未给实验所验证。事实上,有关的实验还没有设计出来。弦论是否真的与原来设想的那样描述自然,还是言之过早。
欧洲核子研究组织(CERN) 日内瓦实验室的大型强子对撞机,或许可以找到余维空间或者超对称粒子存在的线索。这些发现可以和弦论相容,但不足以证明其正确性。
如果要给弦论打分的话,从好的方面来说,弦论启发了某些极之精妙而有力的数学理论,从中获得的数学式子已经有了严格的证明,弦论的对错与否,都不能改变其真确性。弦论纵使还没有为实验所证实,它始终是现存的唯一能够统一各种自然力的完整理论,而且它非常漂亮。试图统一各种自然力的尝试,竟然导致不同数学领域的融合,这是从来没有想过的。
当然,现在要作总结还不是时候,过去两千年间,几何学屡经更替,最终形成今天的模样。而每次重要的转变,都基于人类对大自然的崭新了解,这应当归功于物理学的最新进展。我们或将亲眼看到 21 世纪的重要发展,即量子几何的面世,这门几何未来将把细小的量子物理和大范围的广义相对论结合起来。
抽象的数学为何能够揭露大自然如许讯息,实在不可思议,令人惊叹不已,《大宇之形》一书的主旨乃在于此。不仅如此,我们还希望透过本书,使读者知道数学家是如何进行研究的。他们不必是奇奇怪怪的人,就像在电影《心灵捕手》(Good Will Hunting)中的清洁工般,一面在打扫地板,另一面却破解了悬空百年的数学难题。杰出的数学家也不必如另一部电影和小说《美丽心灵》(A Beautiful Mind)描述的那样,是个精神异常、行为古怪的人。
数学家和做实验的学者同样研究自然,但他们采用的观点不同,前者更为抽象。然而,无论数学家或物理学家,他们的工作都以大自然的真和美为依归。数学和物理互动时迸发的火花,重要的想法如何相互渗透,伟大的新学说如何诞生,如此种种,我们都在书中娓娓道来。
就弦论而言,我们看到几何和物理如何走在一起,催生了美妙的数学与精深的物理。这些数学是如此的美妙,影响了不同的领域,使人们相信它在物理中必有用武之地。可以肯定的是,故事还会继续下去。本人能在其中担当一角色,与有荣焉。今后并将倾尽心血,继续努力。
本文转载自微信公众号数理人文(ID math_hmat)。版权归原作者所有。
推荐阅读
微分几何入门与广义相对论(第二版)上中下册
《上册》:共10章。前5章讲授微分几何入门知识,第6章以此为工具剖析狭义相对论,第7~10章介绍广义相对论的基本内容。本书强调低起点(大学物理系本科2~3年级水平),力求化难为易,深入浅出,为降低难度采取了多种措施。本书适用于物理系高年级本科生、研究生和物理工作者,特别是相对论研究者。不关心相对论而想学习近代微分几何的读者也可把本书前5章作为入门阶梯。
《中册》:包含4章(第11-14章)和6个附录(附录B~G)。第11~13章依次介绍时空的整体因果结构、渐近平直时空和Kerr-Newman黑洞,第14章详细讲述与参考系有关的各种问题,包括时空的3+1分解。附录B和C分别简介量子力学的数学基础和几何相,附录D和E分别介绍能量条件和奇性定理,附录F讲述微分几何很重要的Frobenius定理,附录G则用微分几何语言比较详细地讨论了李群和李代数的知识,并专辟一节介绍对物理学特别重要的洛伦兹群和洛伦兹代数。本册仍然贯彻上册深入浅出的写作风格,为降低读者阅读难度采取了多种措施。
《下册》:包含两章(第15及16章)和三个附录(附录H,I,J)第15章讲授拉氏和哈氏理论,第16章介绍黑洞(热)力学,包括传统(稳态)黑洞热力学及其后续发展,特别是比较详细地讲解了(弱)孤立视界和动力学视界等重要概念,并对近代有关文献的许多公式给出了详细的推证,附录H讲授Noether定理的证明(包括用几何语言和坐标语言的证明)以及有关问题(例如正则能动张量),附录I讲授对理论物理工作者非常有用的主纤维丛和伴纤维丛,并着意于这些数学知识与物理应用之间的“架桥”工作。附录介绍德西特时空和反德西特时空本册仍然贯彻上册深入浅出的写作风格,为降低难度采取了多种措施。
(本期编辑:安 静)
一起阅读科学!
科学出版社│微信ID:sciencepress-cspm
专业品质 学术价值
原创好读 科学品味