打破Batch Size的玄学！有关 batch size 的设置范围，其实不必那么拘谨

会员服务 ·

打破Batch Size的玄学！有关 batch size 的设置范围，其实不必那么拘谨

2022 年 7 月 14 日 极市平台

↑ 点击蓝字关注极市平台

作者丨机器之心

来源丨机器之心

编辑丨极市平台

极市导读

GPU 对 2 的幂次的 batch 可以发挥更好性能？今天来打破这个认知！著名机器学习博主用理论推导和实验结果证明：选择批大小作为 2 的幂或 8 的倍数在实践中会并不会产生明显的差异。 >>加入极市CV技术交流群，走在计算机视觉的最前沿

我们知道，batch size 决定了深度学习训练过程中，完成每个 epoch 所需的时间和每次迭代（iteration）之间梯度的平滑程度。batch size 越大，训练速度则越快，内存占用更大，但收敛变慢。

又有一些理论说，GPU 对 2 的幂次的 batch 可以发挥更好性能，因此设置成 16、32、64、128 … 时，往往要比设置为其他倍数时表现更优。

后者是否是一种玄学？似乎很少有人验证过。最近， 威斯康星大学麦迪逊分校助理教授，著名机器学习博主 Sebastian Raschka 对此进行了一番认真的讨论。

前言

关于神经网络训练，我认为我们都犯了这样的错误：我们选择批量大小为 2 的幂，即 64、128、256、512、1024 等等。（这里，batch size 是指当我们通过基于随机梯度下降的优化算法训练具有反向传播的神经网络时，每个 minibatch 中的训练示例数。）

据称，我们这样做是出于习惯，因为这是一个标准惯例。这是因为我们曾经被告知，将批量大小选择为 2 的幂有助于从计算角度提高训练效率。

这有一些有效的理论依据，但它在实践中是如何实现的呢？在过去的几天里，我们对此进行了一些讨论，在这里我想写下一些要点，以便将来参考。我希望你也会发现这很有帮助！

理论背景

在看实际基准测试结果之前，让我们简要回顾一下将批大小选择为 2 的幂的主要思想。以下两个小节将简要强调两个主要论点： 内存对齐和浮点效率。

内存对齐

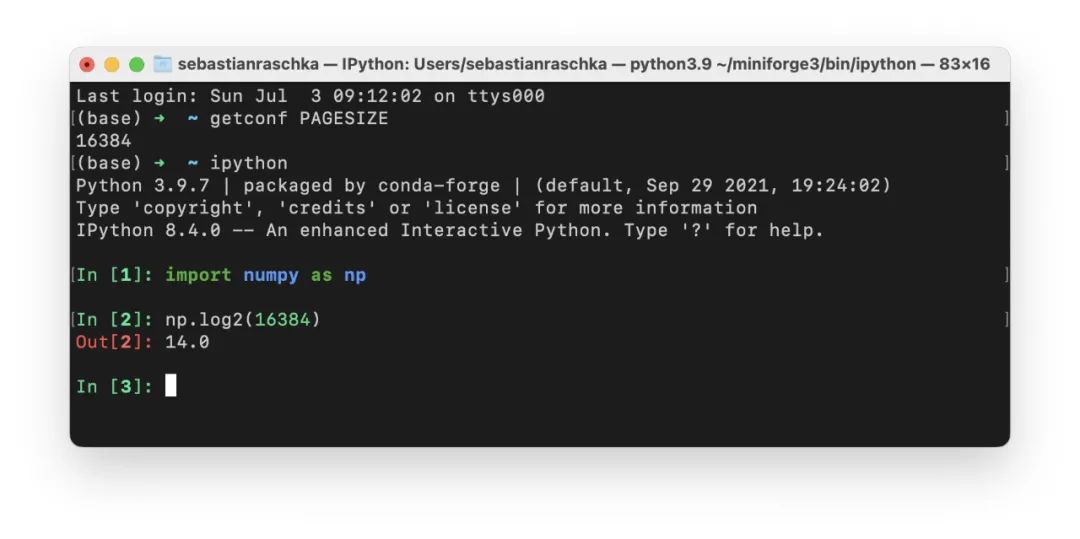
选择批大小为 2 的幂的主要论据之一是 CPU 和 GPU 内存架构是以 2 的幂进行组织的。或者更准确地说，存在内存页的概念，它本质上是一个连续的内存块。如果你使用的是 macOS 或 Linux，就可以通过在终端中执行 getconf PAGESIZE 来检查页面大小，它应该会返回一个 2 的幂的数字。

这个想法是将一个或多个批次整齐地放在一个页面上，以帮助 GPU 并行处理。或者换句话说，我们选择批大小为 2 以获得更好的内存对齐。这与在视频游戏开发和图形设计中使用 OpenGL 和 DirectX 时选择二次幂纹理类似。

矩阵乘法和 Tensor Core

再详细一点，英伟达有一个矩阵乘法背景用户指南，解释了矩阵尺寸和图形处理单元 GPU 计算效率之间的关系。因此，本文建议不要将矩阵维度选择为 2 的幂，而是将矩阵维度选择为 8 的倍数，以便在具有 Tensor Core 的 GPU 上进行混合精度训练。不过，当然这两者之间存在重叠：

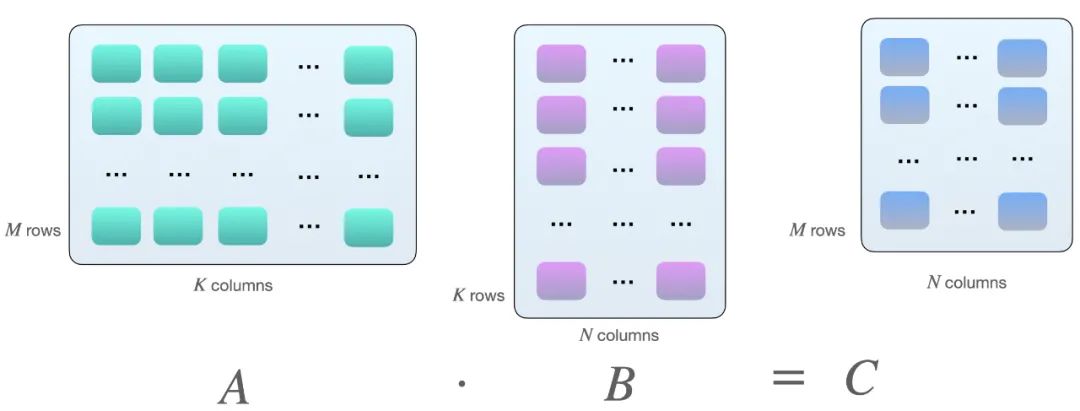
为什么会是 8 的倍数？这与矩阵乘法有关。假设我们在矩阵 A 和 B 之间有以下矩阵乘法：

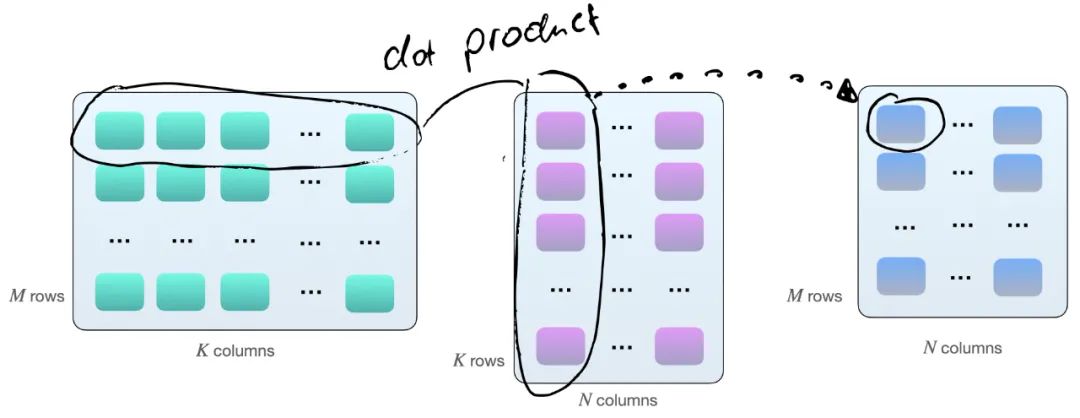
将两个矩阵 A 和 B 相乘的一种方法，是计算矩阵 A 的行向量和矩阵 B 的列向量之间的点积。如下所示，这些是 k 元素向量对的点积：

每个点积由一个「加」和一个「乘」操作组成，我们有 M×N 个这样的点积。因此，共有 2×M×N×K 次浮点运算（FLOPS）。不过需要知道的是：现在矩阵在 GPU 上的乘法并不完全如此，GPU 上的矩阵乘法涉及平铺。

如果我们使用带有 Tensor Cores 的 GPU，例如英伟达 V100，当矩阵维度 (M、N 和 K）与 16 字节的倍数对齐（根据 Nvidia 的本指南）后，在 FP16 混合精度训练的情况下，8 的倍数对于效率来说是最佳的。

通常，维度 K 和 N 由神经网络架构决定（尽管如果我们自己设计还会有一些回旋余地），但批大小（此处为 M）通常是我们可以完全控制的。

因此，假设批大小为 8 的倍数在理论上对于具有 Tensor Core 和 FP16 混合精度训练的 GPU 来说是最有效的，让我们研究一下在实践中可见的差异有多大。

简单的 Benchmark

为了解不同的批大小如何影响实践中的训练，我运行了一个简单的基准测试，在 CIFAR-10 上训练 MobileNetV3 模型 10 个 epoch—— 图像大小调整为 224×224 以达到适当的 GPU 利用率。在这里，我使用 16 位原生自动混合精度训练在英伟达 V100 卡上运行训练，它更有效地使用了 GPU 的张量核心。

如果想自己运行它，代码可在此 GitHub 存储库中找到：https://github.com/rasbt/b3-basic-batchsize-benchmark

小 Batch Size 基准

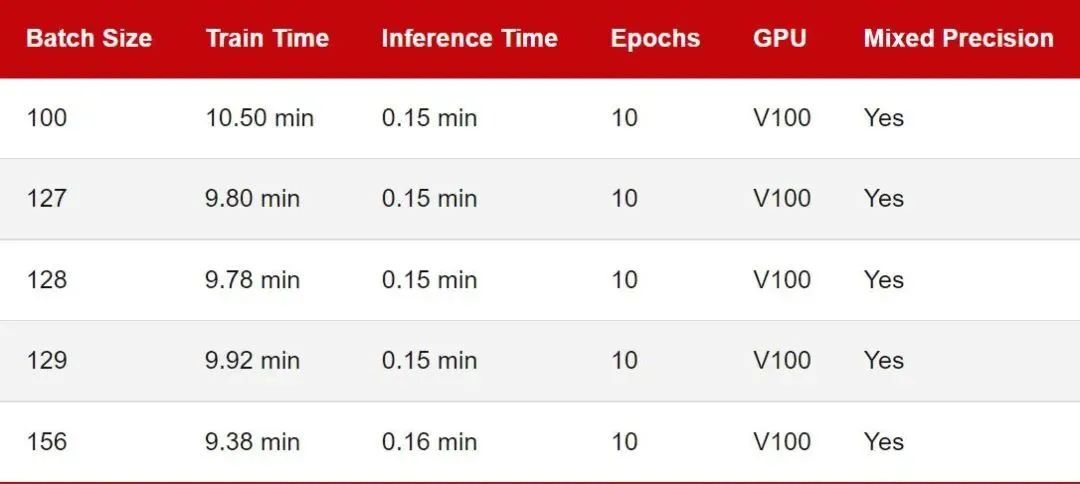
我们从批大小为 128 的小基准开始。「训练时间」对应于在 CIFAR-10 上训练 MobileNetV3 的 10 个 epoch。推理时间意味着在测试集中的 10k 图像上评估模型。

查看上表，让我们将批大小 128 作为参考点。似乎将批量大小减少一 (127) 或将批量大小增加一 (129) 确实会导致训练性能减慢。但这里的差异看来很小，我认为可以忽略不计。

将批大小减少 28 (100) 会导致性能明显下降。这可能是因为模型现在需要处理比以前更多的批次（50,000 / 100 = 500 对比 50,000 / 100 = 390）。可能出于类似的原因，当我们将批大小增加 28 (156) 时就可以观察到更快的训练时间。

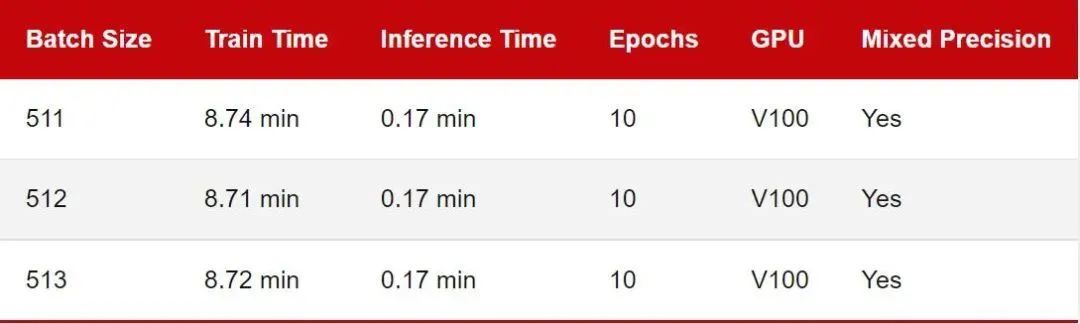
最大 Batch Size 基准

鉴于 MobileNetV3 架构和输入图像大小，上一节中的批尺寸相对较小，因此 GPU 利用率约为 70%。为了研究 GPU 满负荷时的训练时间差异，我将批量大小增加到 512，以使 GPU 显示出接近 100% 的计算利用率：

由于 GPU 内存限制，批大小不可能超过 515。

同样，正如我们之前看到的，作为 2 的幂（或 8 的倍数）的批大小确实会产生很小但几乎不明显的差异。

多GPU训练

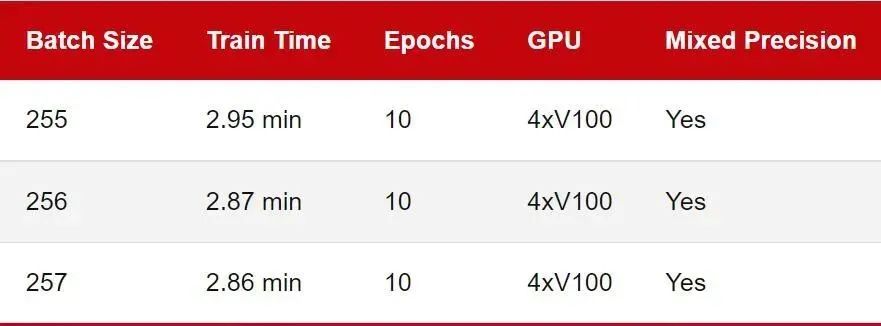
之前的基准测试评估了单块 GPU 上的训练性能。不过如今在多 GPU 上训练深度神经网络更为常见。所以让我们看看下面的多 GPU 训练的数字比较：

请注意，推理速度被省略了，因为在实践中我们通常仍会使用单个 GPU 进行推理。此外，由于 GPU 的内存限制，我无法运行批处理大小为 512 的基准测试，因此在这里降低到 256。

正如我们所看到的，这一次 2 的幂和 8 的倍数批量大小 (256) 并不比 257 快。在这里，我使用 DistributedDataParallel (DDP) 作为默认的多 GPU 训练策略。你也可以使用不同的多 GPU 训练策略重复实验。GitHub 上的代码支持 —strategy ddp_sharded (fairscale)、ddp_spawn、deepspeed 等。

基准测试注意事项

这里需要强调的是上述所有基准测试都有注意事项。例如我只运行每个配置一次。理想情况下，我们希望多次重复这些运行并报告平均值和标准偏差。（但这可能不会影响我们的结论，即性能没有实质性差异）

此外，虽然我在同一台机器上运行了所有基准测试，但我以连续的顺序运行它们，运行之间没有很长的等待时间。因此这可能意味着基本 GPU 温度在运行之间可能有所不同，并且可能会对计时产生轻微影响。

我运行基准测试来模仿真实世界的用例，即在 PyTorch 中训练具有相对常见设置的现成架构。然而，正如 Piotr Bialecki 正确指出的那样，通过设置 torch.backends.cudnn.benchmark = True 可以稍微提高训练速度。

其他资源和讨论

正如 Ross Wightman 所提到的，他也不认为选择批量大小作为 2 的幂会产生明显的差异。但选择 8 的倍数对于某些矩阵维度可能很重要。此外 Wightman 指出，在使用 TPU 时批量大小至关重要。（不幸的是，我无法轻松访问 TPU，也没有任何基准比较）

如果你对其他 GPU 基准测试感兴趣，请在此处查看 Thomas Bierhance 的优秀文章：https://wandb.ai/datenzauberai/Batch-Size-Testing/reports/Do-Batch-Sizes-Actually-Need-to-be-Powers-of-2---VmlldzoyMDkwNDQx

特别是你想要比较：

显卡是否有 Tensor Core；
显卡是否支持混合精度训练；
在像 DeiT 这样的无卷积视觉转换器。

Rémi Coulom-Kayufu 的一个有趣的实验表明，2 次方的批大小实际上很糟糕。看来对于卷积神经网络，可以通过以下方式计算出较好的批大小：

Batch Size=int ((n×(1<<14)×SM)/(H×W×C))。

其中，n 是整数，SM 是 GPU 内核的数量（例如，V100 为 80，RTX 2080 Ti 为 68）。

结论

根据本文中共享的基准测试结果， 我不认为选择批大小作为 2 的幂或 8 的倍数在实践中会产生明显的差异。

然而，在任何给定的项目中，无论是研究基准还是机器学习的实际应用上，都已经有很多旋钮需要调整。因此，将批大小选择为 2 的幂（即 64、128、256、512、1024 等）有助于使事情变得更加简单和易于管理。此外，如果你对发表学术研究论文感兴趣，将批大小选择为 2 的幂将使结果看起来不像是刻意挑选好结果。

虽然坚持批大小为 2 的幂有助于限制超参数搜索空间，但重要的是要强调批大小仍然是一个超参数。一些人认为较小的批尺寸有助于泛化性能，而另一些人则建议尽可能增加批大小。

个人而言，我发现最佳批大小在很大程度上取决于神经网络架构和损失函数。例如，在最近一个使用相同 ResNet 架构的研究项目中，我发现最佳批大小可以在 16 到 256 之间，具体取决于损失函数。

因此，我建议始终考虑调整批大小作为超参数优化搜索的一部分。但是，如果因为内存限制而不能使用 512 的批大小，则不必降到 256。有限考虑 500 的批大小是完全可行的。

原文链接

https://sebastianraschka.com/blog/2022/batch-size-2.html

公众号后台回复“目标检测综述”获取目标检测（2001-2021）综述PDF～

△点击卡片关注极市平台，获取最新CV干货

极市干货

最新数据集资源：医学图像开源数据集汇总（二）

技术解读：一文打尽NMS技术的种种｜这是一篇对YOLOv7的详细解读和剖析

极视角动态：青岛日报专访｜极视角陈振杰：创业的每一个决定都要经得起逻辑推演｜启动报名｜2022GCVC全球人工智能视觉产业与技术大会，7月22日青岛见！