基于信息传递框架的图自编码范式

2020 年 12 月 7 日 图与推荐

本系列首先会介绍王翔老师^[1]和何向南老师^[2]在WSDM 2020/CIKM 2019上的Tutorial^[3]：「Learning and Reasoning on Graph for Recommendation」中所涉及的“基于「信息传递框架」的图自编码范式”，即：基于信息传递框架来做结点的图表征。这个范式能够将GNN各组件拆解开来，并各自迭代和优化，对于模型优化迭代和编程实践有非常好的启发。

后续我会基于这样的范式，重新梳理图表示学习在推荐系统中常见的用户-物品交互数据上的建模方法。我们可以将用户-物品的交互数据看做是关于user-item的二分图(Bipartite Graph)，这样可以基于GNN的方法进行user和item嵌入的学习。我将重点探讨如何基于「信息传递框架」来拆解目前主流的二分图表示学习方法，不同的方法是如何针对不同的组件做改进和迭代，我会对8篇顶会文章的改进脉络做一个系统性地梳理。

本篇文章将主要介绍基于信息传递框架的图自编码范式。

1. Message-Passing信息传递框架

在之前的文章万字长文 | 图表示学习中的Encoder-Decoder框架中，我们介绍了一种应用于图表示学习的Encoder-Decoder框架。该框架是对所有「图表示学习的方法」的「所有过程」的抽象，即：编码，解码，相似性度量和损失函数。而其中最重要的步骤是「Encoder」，实际上，「大部分方法主要的差异只体现在Encoder上」，其它三种都大同小异，比如GraphSAGE和GATs。因此，如何对Encoder进一步做抽象就显得很重要了。

信息传递框架就是为Encoder的进一步抽象所服务的，也是近年来大部分GNN工作所采用的设计范式。信息传递框架最早是在ICML 2017，Neural Message Passing for Quantum Chemistry^[8]中被提出来，作者在这篇论文将现有神经网络模型抽象出其共性并提出一种信息传递神经网络框架(Message Passing Neural Networks, MPNN)，同时利用 MPNN 框架在分子分类预测中取得了一个不错的成绩。MPNN包括了两个阶段：「信息传递阶段(Message Passing)」 和 「读出阶段(Readout)」。其中，信息传递阶段可以细分为信息构建、信息汇聚和信息更新，得到每个结点的表征。读出阶段是指系统更新多次达到某个状态后，从图中的所有结点状态映射得到Graph-Level的表征(原文是做分子分类预测，因此需要得到Graph表征)。

我们这里讨论的是Node-Level的表征，因此可以借鉴「信息传递阶段」。图神经网络GNN在设计Encoder的时候，会做基于邻域汇聚的卷积操作，涉及到的卷积操作会有很多步骤，可以采用Message-Passing信息传递框架来组织和提炼其中的核心步骤，并封装成各个组件，每个组件都能够「单独进行设计和改进」。这些组件包括：「信息构建组件」，「邻域汇聚组件」和「表征更新组件」。

信息构建组件：负责构建从邻域结点到目标结点「要传递」的信息；
邻域汇聚组件：负责「汇聚」从邻域结点集合传递到目标结点的信息；
表征更新组件：负责将从邻域结点集合中收集到的信息和本身的信息做一个「融合和更新」。

上述3个步骤构成了一个完整的迭代步。第一步迭代结束后，每个结点都融合了一阶的邻域结点的信息；依次类推，多次迭代，就能够融合多阶的邻域结点信息。值得一提的是，著名的图学习框架DGL^[7]就是基于消息传递框架来组织和设计代码，下面依次介绍各个组件。

1.1 信息构建组件

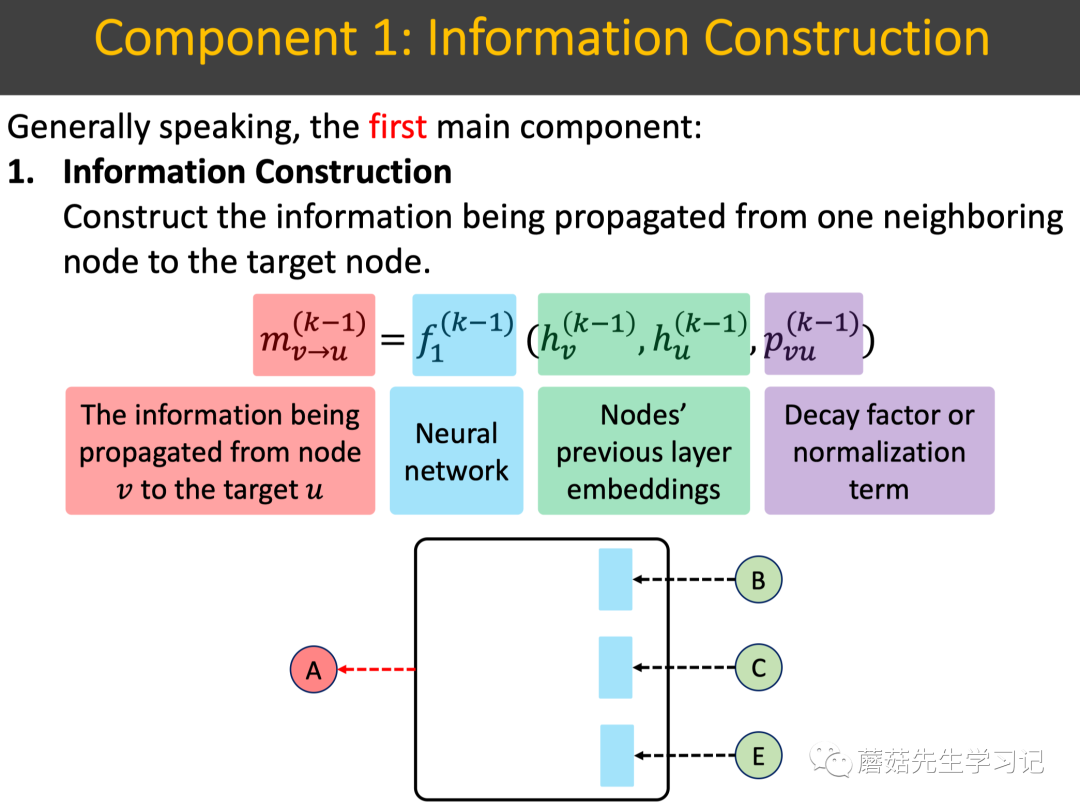
「Information Construction」 信息构建组件：构建从「1个邻域结点」到「目标结点」要「传递的信息」。

如下图所示，信息构建组件使用「信息构建网络」，「输入数据」是前一层的目标结点和邻域结点的表征，还有个decay系数/正则化项，表示信息传递过程中的「衰减系数」，「输出数据」是从邻域结点到目标结点要传递的信息。总结起来，这里头核心的组成元素包括：

「输入数据」：前一层的目标结点和邻域结点的表征。
「输出数据」：从1个邻域结点到目标结点要传递的信息。
「decay系数/正则化项」：信息传递过程中的衰减系数。这个系数在基于二分图的推荐系统中非常重要，例如可以用结点的度的倒数来表示物品的流行度衰减因子或者用户的活跃度衰减因子。
「信息构建网络」：基于输入数据和decay系数，来构建要传递的信息。最简单，信息构建网络为，即：传递的信息为邻域结点表征，衰减系数为1。

信息构建组件

1.2 邻域汇聚组件

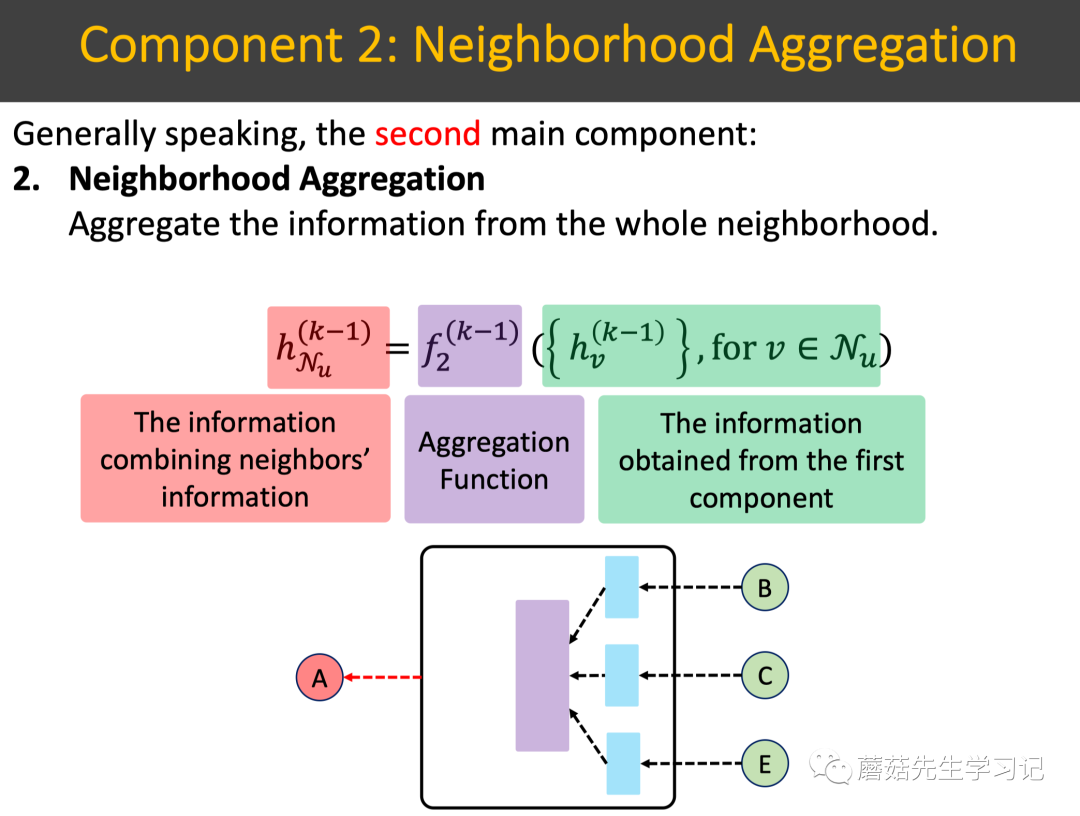
「Neighborhood Aggregation」 邻域汇聚组件：基于上述构建好的每个邻域结点要传递的信息，来「汇聚所有」的邻域结点的信息。

如下图所示，邻域汇聚使用「汇聚函数」，其输入是上述构建好的信息；输出是「汇聚好的所有邻域的信息」。总结下核心的组成元素：

「输入数据」：目标结点的邻域集合中的结点从1.1信息构建组件中构建好的信息。
「输出数据」：汇聚好的邻域信息，或者说从邻域结点集合传递到目标结点的信息。
「汇聚函数」：汇聚函数实际上也可以用汇聚网络来表示，即：既可以设计简单的汇聚函数，如mean pooling，sum pooling，attention等，也可以设计复杂的汇聚网络，如attention网络。

邻域汇聚组件

1.3 表征更新组件

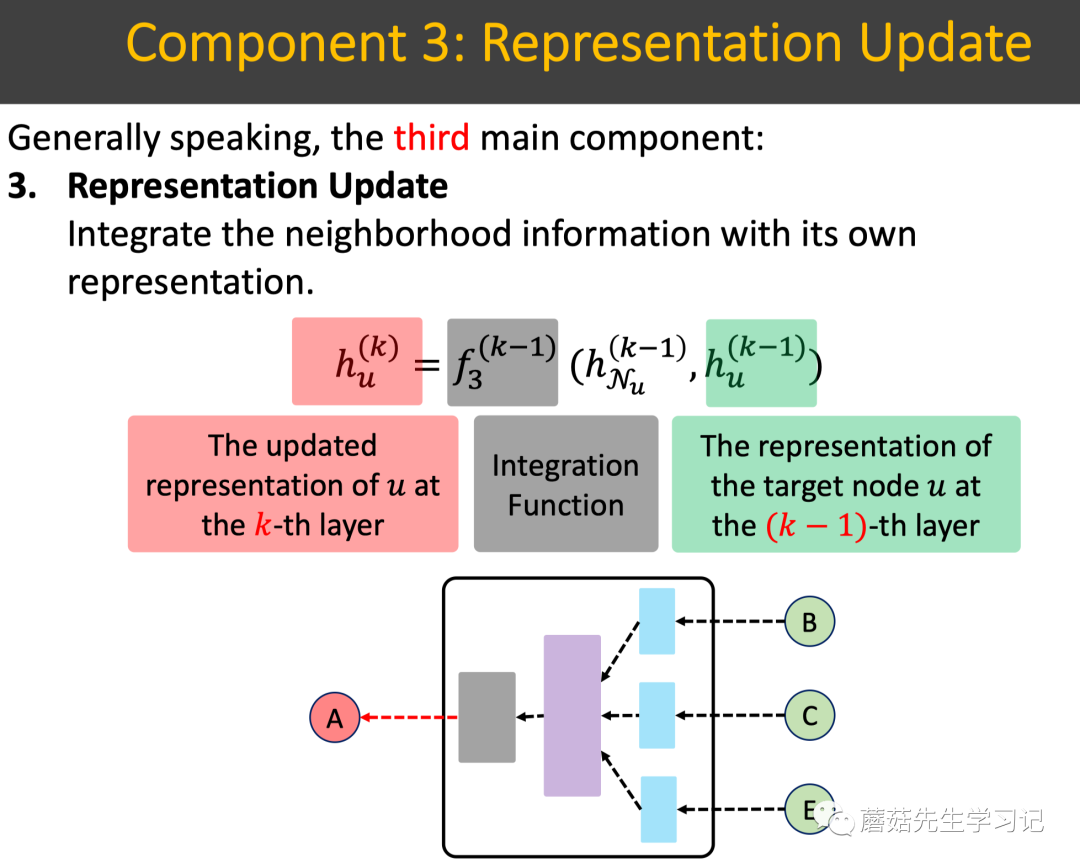
「Representation Update」：表征更新组件：融合从「邻域集合汇聚到的信息」和「自己本身的信息」，来做自我表征的更新。

如下图所示，表征更新使用融合函数，输入是步骤1.2中汇聚到的邻域信息以及结点本身的信息，输出是结点新的表征。比如：融合函数可以使用sum操作或者concat+非线性变换操作。总结下核心组成元素：

「输入数据」：步骤1.2中汇聚到的邻域集合信息，结点本身的信息，
「输出数据」：目标结点更新后的表征，此时表征所代表的阶数提高了一阶。
「融合函数」：融合函数既可以使用简单的sum操作或者concat+非线性变换操作，也可以使用复杂的融合网络来融合。

表征更新组件

2. 信息传递框架范式案例

下面以GraphSAGE[4]和GATs[5]为例，来介绍这两个主流的GNN模型中Encoder结构拆解示例。

2.1 GraphSAGE

2.1.1 信息构建组件

即：传递的信息为邻域结点表征。

2.1.2 邻域汇聚组件

其中Agg汇聚函数在GraphSAGE中有多种形式。

「Mean Aggregator」: ，即：element-wise mean of the vectors.
「GCN Aggregator」: 这个是GCN中矩阵形式乘法的等价形式。细节推导可参见：万字长文 | 图表示学习中的Encoder-Decoder框架中的GraphSAGE一节。
「LSTM aggregator」: 直接对邻域节点随机扰动permutation，然后将扰动后的序列使用LSTM来聚合。感觉有点简单粗暴了。
「Pooling aggregator」：

即：每个邻居节点的表示先经过一个MLP，然后进行sigmoid激活；最后应用element-wise max pooling策略，此处的max pooling，作者提到用mean pooling也是可以的。内部的MLP也可以改成多层的MLP。

2.1.3 表征更新组件

即：2.1.2邻域汇聚得到的信息做一个线性变换；目标结点在前一层的表征做一个线性变换；二者拼接起来，过一个激活函数，得到更新后的第阶表征。

上述核心的邻域汇聚组件和表征更新组件总结下来如下图所示：

GraphSAGE信息传递框架示例

2.2 GATs

2.2.1 信息构建组件

同GraphSAGE。即：传递的信息为邻域结点表征。

2.2.2 邻域汇聚组件

基于注意力框架的邻域汇聚组件。引入了self-attention机制，每个节点attend到自身的邻域节点上。不同于GraphSAGE采用Mean/Pooling Aggregator，GATs采用了基于self-attention机制的Aggregator。也就是说，把目标节点的表示和邻域节点的表示通过一个注意力网络，计算注意力值，再依据该注意力值来汇聚邻域节点。对于节点 $u$ 及其邻域节点 $v$ 。我们要计算 $u$ 节点attend到 $v$ 的注意力值，attention score计算如下：

先对和的前一层的表征做一个线性变换 (即multi-head attention的特例，1-head attention)，。
再把变换后的表示送到attention网络并进行softmax得到注意力值，

这个attention网络结构如下：

即：二者拼接到一起后，经过一个线性变换 (attention网络的参数)，再LeakyReLU激活。

则Aggregator直接依注意力值对线性变换后的向量加权并激活即可：

2.2.3 邻域汇聚组件

实际上，GATs中的邻域汇聚组件和表征更新组件是可以合在一起实现的。即：对于节点和自身的attention score，作者提到直接代入即可。这样，统一公式：

另外，作者提到，可以采用multi-head attention来拓展，即：2.2.2中attention score计算的第一步中，将node feature变换到不同的语义子空间，再进行attention score计算并汇聚。每个head输出一个，将所有的输出拼接到一起；或者做mean pooling，作为节点更新后的表征。

上述核心的邻域汇聚组件和表征更新组件总结下来如下图所示：

GATs信息传递框架示例

总结

本文讨论了WSDM 2020/CIKM 2019上王翔老师分享的关于「信息传递框架的图自编码器范式」，并介绍了如何基于这种范式，对GraphSAGE和GATs中的Encoder进行重新提炼和组织。

后续我会基于这样的范式，重新梳理「图表示学习在推荐系统」中常见的用户-物品交互数据上的建模。我将重点探讨如何基于「信息传递框架」来拆解目前主流的「二分图表示学习」方法，即：不同的方法是如何针对不同的组件做改进和迭代以及不同的方法间有什么区别和联系，我将在以后的文章中分享的8篇顶会工作如下，「敬请期待」。