一文掌握深度学习卷积结构

来源：卷积大全

这篇文章，对三种不同卷积的优缺点进行了详细的介绍。

▍卷积

首先，定义一下卷积层的参数。

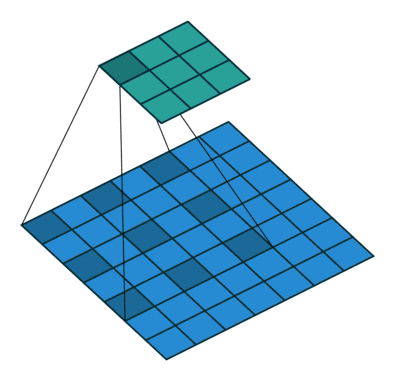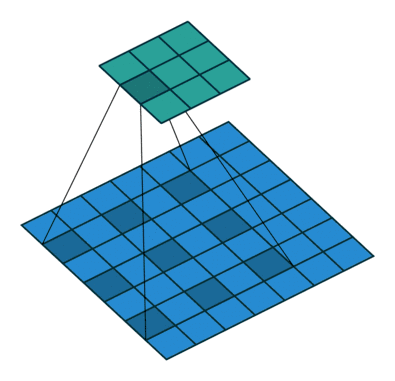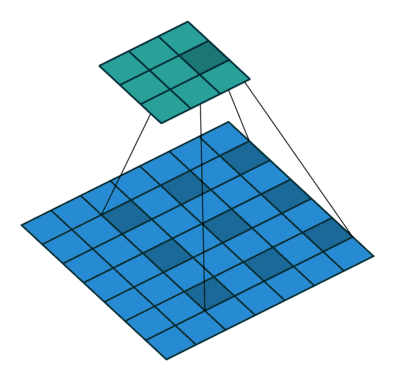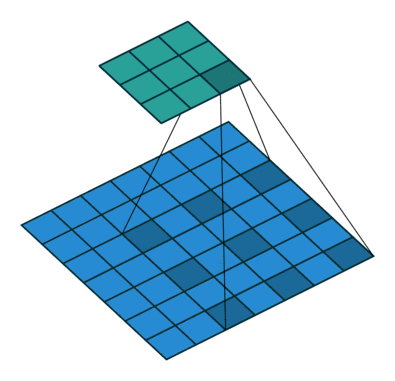
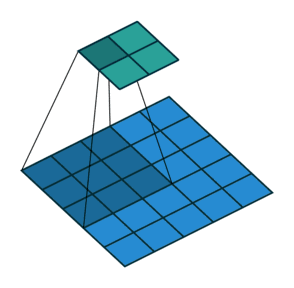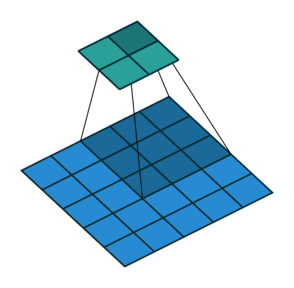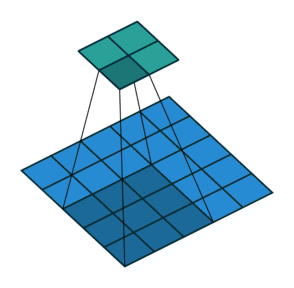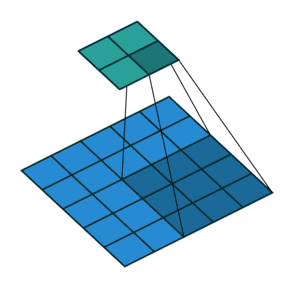
△kernel 为 3、stride 为 1，利用 padding 的 2D 卷积

• 卷积核大小：卷积核决定了卷积的视野。在2D卷积中，常见卷积核为 3，即 3x3 像素

• stride：stride 决定卷积核遍历图像时的步幅大小。默认值通常为 1，我们可以将 stride 设置成 2，对图像进行类似最大池化的下采样

• Padding：padding 决定处理样本时的边界。（半）填充的卷积使输出空间维度等于输入，而未填充的卷积会裁剪部分边界，如果卷积核大于 1 的话。

• 输入&输出通道：卷积层通常需要一定数量的输入通道 (I)，计算一定数量的输出通道 (O)。所需参数可以通过 IOK 来计算，K 就是卷积核的值。

▍空洞卷积

△kernel 为 3、扩张率为 2、无边界扩充的 2D 卷积

扩张卷积向卷积层引入另一个参数扩张率，它决定了卷积核中值之间的空间。3x3 卷积核、扩张率为 2 的卷积视野和 5x5 卷积核的视野相同，并且前者仅使用了 9 个参数。想象一个 5x5 的卷积核，每个都删去第二行和第二列。

这种卷积用同样的计算成本生成了更大的视野。扩张卷积在实时分隔领域中尤为流行。如果你需要一个宽阔视野，但无力使用多个卷积或更大的卷积核，那么你可以使用这种卷积。

▍转置卷积

解卷积（deconvolution）这种叫法不太合适，因为这并不是解卷积。解卷积确实存在，但在深度学习领域中并不常见。真正的解卷积是卷积过程的逆转。

想象一下将一个图像输入到单个卷积层上。再把输出放到黑箱中，然后再次输出的是原始输入图像。这个黑箱就叫作解卷积。这是卷积层执行的数学逆运算。

转置卷积与解卷积有一些相似，因为它所输出的空间分辨率反卷积层也能够输出。但是，在这些值上真正进行的数学运算是不一样的。转置卷积层使用的是常规的卷积，但仍然能够进行空间分辨率转换。

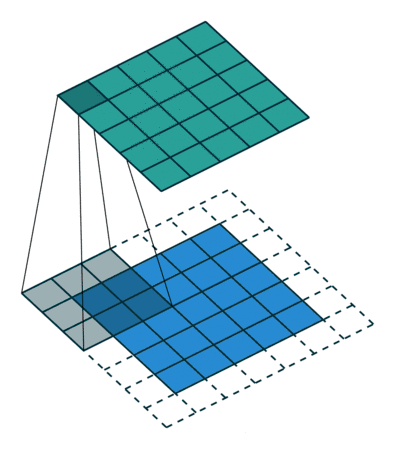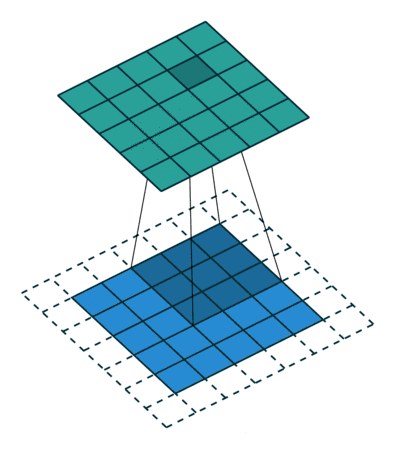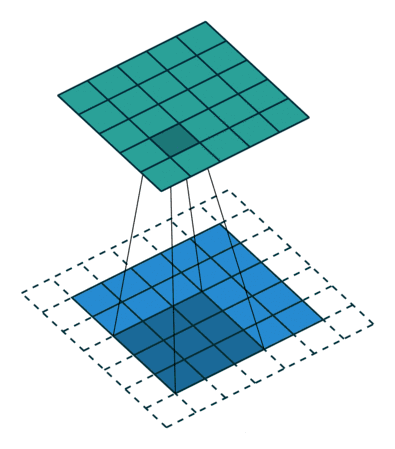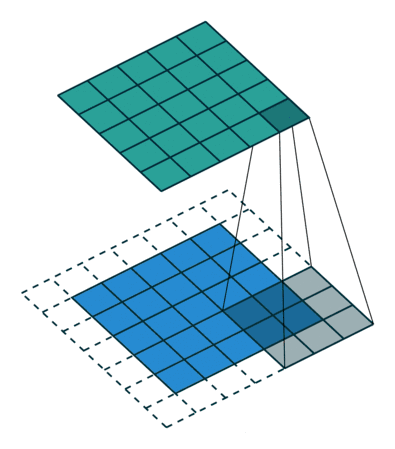
△stride 为 2、卷积核为 3 的 2D 卷积和无边界扩充卷积

一个 5x5 的图像输入到卷积层中，stride 设置为 2，没有 padding，卷积核为 3x3。输出的是 2x2 的图像。

如果我们想逆转该过程，则我们需要进行数学逆运算，以使我们输入的每个像素都能够生成 9 个值。之后，我们用值为 2 的 stride 遍历输出图像。这就是解卷积。

转置卷积并不这么做。二者唯一的共同点是输出的都是 5x5 的图像，虽然它执行的仍旧是常规的卷积运算。为了做到这一点，我们需要在输入上执行某种 padding。

如同你能想象的，这一步不会从顶部逆转该流程，至少在数值方面不会实现逆转。

它只不过是从前面重建了空间分辨率，且完成一个卷积。这可能不是数学意义上的逆转，但对编码器-解码器架构而言，它仍旧非常有帮助。通过这种方式，我们可以将卷积和图像的 upscaling 结合起来，而不是执行两个独立的流程。

▍可分离卷积

在可分离卷积中，我们能把卷积核运算分离到多个步骤中。

例如，我们可以把一种卷积表达为 y = conv(x, k)，其中 y 是输出图像，x 是输入图像，k 是卷积核。下面，假设 k 按 k = k1.dot(k2) 进行计算。这样可使其成为可分离卷积，因为我们不再使用 k 做 2D 卷积，而是通过用 k1 和 k2 做两个 1D 卷积得到同样的结果。

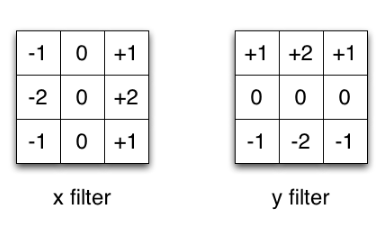
△X 与 Y 滤波器

以经常用于图像处理的 Sobel 核为例。你可以通过乘以向量 [1, 0, -1] 和 [1,2,1] 的转置向量获得相同的核。在进行相同操作时，这只需要 6 个参数，而无需 9 个。

上述实例展示了空间可分离卷积，据我所知它并不用于深度学习。我只是想让大家在看到这个术语时不会感到困惑。在神经网络中，我们通常使用深度可分离卷积（depthwise separable convolution）。

这种卷积将执行空间卷积，同时保持通道分离，接着跟从深度卷积。为了便于理解，我们来看一个实例。

假设我们在 16 个输入通道和 32 个输出通道上有一个 3x3 卷积层。每一个输入通道都由 32 个 3x3 内核遍历，产生 512（16x32）个特征图。下一步，我们通过叠加每一个输入通道中的特征图，合并形成一个特征图。由于我们这样做了 32 次，我们得到了 32 个想要的输出通道。

对于相同实例上的深度可分离卷积，我们遍历了 16 个通道（每个带有一个 3x3 内核），得到了 16 个特征图。

现在，在合并之前，我们遍历了这 16 个特征图（每个带有 32 个 1x1 卷积），然后再把它们叠加在一起。相比于上述的 4608（16x32x3x3）个参数，这产生了 656（16x3x3 + 16x32x1x1）个参数。

该实例是深度可分离卷积的特定实现，深度乘数是 1，这是目前这类卷积层的最常见设置。

这么做是因为假设空间和深度信息可被解耦。看 Xception 模型的表现，该方法似乎是有效的。因其对参数的高效使用，深度可分离卷积也可被用于移动设备。

更多卷积：https://github.com/vdumoulin/conv_arithmetic

点击下方“阅读原文”下载同声译
↓↓↓