秒懂“线性回归预测”
线性回归是机器学习中的概念,线性回归预测算法一般用以解决“使用已知样本对未知公式参数的估计”类问题。
举个栗子:
商家卖鞋,可利用历史上每个季度鞋的定价x与销量y,来预估“定价与销量的关系”(y=ax+b),以辅助对鞋子进行最佳定价。
一、几个基本概念
回归(regression):用已知样本对未知公式参数的估计。Y=f(X1, X2, X3),这里回归函数f(X1, X2, X3)可能是任意函数。
线性回归(linear regression):回归的一种,回归函数是一次函数,例如:
Y=f(X1, X2, X3)=aX1 + bX2 + cX3 + d
其中X1,X2,X3是训练样本集中样本的各个维度(feature),a,b,c,d是模型的未知参数。
逻辑回归(logistic regression):将Y归一化到[0, 1]区间。
总而言之,逻辑回归是线性回归的一种,线性回归是回归的一种。
二、线性回归模型经常是有效的
线性回归有什么用?
答:线性回归的预测模型虽然是一元线性方程,但现实中很多应用场景符合这个模型。
例如例子中商品的定价x与商品的销量y之间的关系。一般来说价格越贵则销量越低,价格越便宜则销量越高,于是就能够用y=ax+b这个评估模型来最大化商家的收益:收益=定价*销量=x*y=x*(ax+b)
什么场景适用于线性回归?
答:很多应用场景不能够使用线性回归模型来进行预测,例如,月份和平均气温,平均气温并不随着月份的增长呈线性增长或下降的趋势。它常用于:
(1)预测或分类,用于分类问题时,需要设定阈值区间,并提前知晓阈值区间与类别的对应关系
(2)线性问题,可以有多个维度(feature)
三、如何求解线性回归中的维度参数?
在已知样本集set的时候,如果根据样本集得到Y=f(X1,X2,X3,…)=aX1+bX2+cX3+…中的未知参数a,b,c呢?
这得先介绍最小二乘法,以及梯度下降法。
什么是最小二乘法?
答:最小二乘法适用于任意多维度的线性回归参数求解,它可求解出一组最优a,b,c解,使得对于样本集set中的每一个样本data,用Y=f(X1,X2,X3,…)来预测样本,预测值与实际值的方差最小。
画外音:方差是我们常见的估值函数(cost function),用来评估回归出来的预测函数效果。
什么是梯度下降法?
答:最小二乘法实际上只定义了估值函数是方差,真正求解a,b,c的方法是梯度下降法,这是一个枚举型的求解算法,其算法步骤如下:
(1)使用随机的a0, b0, c0作为初始值
(2)分别求解最优a, b, c…,对于每个维度参数的求解,步骤为(以a为例):
2.1)设定a范围的最大值与最小值
2.2)设定a计算的梯度步长(这就是它叫梯度下降法的原因)
2.3)固定其他维度参数
2.4)计算a的所有取值中,使得估值函数最小的那个a即为所求
数学上可以证明:
(1)上述算法是可以收敛的(显而易见)
(2)分别求出a,b,c的最优值,组合起来就是整体的最优值(没这么明显了),这个结论是很重要的,假设样本个数为n,计算a,b,c的算法复杂度都是线性的O(m),这个结论让算法的整体复杂度是n*O(m) +n*O(m) + n*O(m),而不是[n*O(m) ]*[n*O(m)]*[n*O(m)]的关系。
画外音:计算机非常适合干这个事情,确定范围和梯度后,这是一个线性复杂度的算法。
四、再来个栗子说明
已知过去4个季度销量与价格的数据样本集为:
价格x为10时,销量y为80
价格x为20时,销量y为70
价格x为30时,销量y为60
价格x为40时,销量y为65
假设销量y与价格x是线性关系:
y=ax +b
假设a的范围为[-2, 2],a的梯度为1
假设b的范围为[80, 120],b的梯度为10
画外音:计算机计算的时候,范围会很大,梯度精度会很细。
求解最优a和b的过程为:
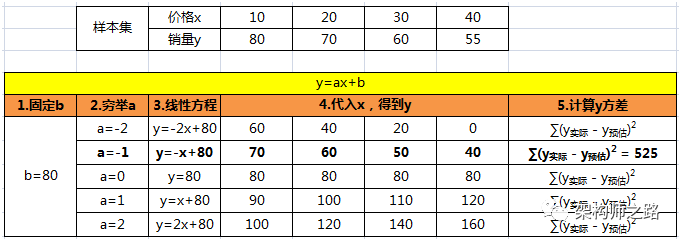
(1)设a0=-2,b0=80,从最边缘开始求解
(2.1)先求最优a,固定b=80不动,a从-2到2梯度递增,求最优a的解
可以看到,a=-1时方差最小,故a=-1是最优解。
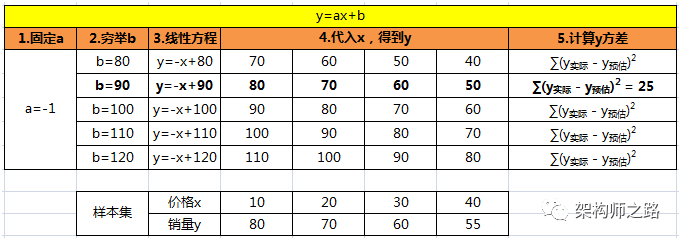
(2.2)再求最优b,固定2.1求出的最优a=-1,b从80到120梯度递增,求最优b的解
可以看到,b=90时方差最小,故b=90是最优解。
(3)得到最优解a=-1,b=90,于是得到定价与销量的关系是:y=-x+90
(4)最终得到
收益=定价*销量=x*y=x*(-x+90)
于是,当价格定在45元时,整体收益能够最大化。
五、总结
逻辑回归是线性回归的一种,线性回归是回归的一种
线性回归可以用在预测或分类,多维度(feature)线性问题求解上
可以用最小二乘法,梯度下降法求解线性预测函数的系数
梯度下降法的核心步骤是:设置系数范围,设定系数梯度,固定其他系数,对某一个系数穷举求方差最小最优解
希望这一分钟,对线性回归预测有了一点点了解。
相关内容: