【人工智能】2019计算与系统神经科学大会Cosyne 前沿研究汇总

2019 年 5 月 3 日 产业智能官

作者：许铁来源：混沌巡洋舰

0 背景

计算神经科学是一门超级跨学科的新兴学科，几乎综合信息科学，物理学，数学，生物学，认知心理学等众多领域的最新成果。关注的是神经系统的可塑性与记忆，抑制神经元与兴奋神经元的平衡。计算神经科学在做的事情是先主动设计这个一个系统，看看如何做到需要的功能（自上而下），然后拿着这个东西回到生物的世界里去比较（由下而上）。人工智能和计算神经科学具有某种内在的同质性，唯一的区别可能是人工智能可以不必拘泥生物的限制，或者也是为什么他最终或许会比生物网络表现更好。

今年的计算与系统神经科学大会 - Cosyne 在葡萄牙结束。这个会议和nips都是神经网络与计算方面的最重要盛会，而方向上一个更偏深度学习，一个更偏和生物有关的计算。而近两年的趋势是，两个会议的交叉主题越来越多。对于会议涵盖的几个方面，做一个小的总结，也算涵盖了计算神经科学的主要方面。

1：前馈网络：如何让深度学习工作更像人脑

在这个session， Yann Lecun 作为邀请演讲人，总结了CNN受生物神经网络启发的历史，并提出他最近的核心方向 - learning predictive model of world（学习建立预测性的模型）。指出深度学习的未来在于以建立预测性模型为核心的半监督学习，这样可以弥补普通的监督学习或model free reinforcement learning（无模型强化学习）的巨大缺陷-缺乏稳定的先验模型。比如你要做一个视频有关的处理，让他看完youtube上的视频并不停的预测视频下一帧的状态，这样预训练后再去进行任何任务都会更方便。 yann认为这是dl的未来方向。

一个目前突出的成就是大量预训练产生的NLP模型Bert在各大任务上都破了记录。关于如何进行半监督学习， auto-encoder和对抗学习都是方向。在此处无监督，监督，和强化学习的界限已经接近。强化学习不再只是蛋糕上的樱桃，无监督学习也不再是难以操作的暗物质。预测性学习用的是监督学习的方法，干的是无监督学习的事情，而最后被用于强化学习。不难看出，这个方法论和计算神经科学领域的predictive coding间的联系，和好奇心的联系。整个工作都符合Karl Friston 关于自由能最小的理论框架。

有关前馈网络和计算神经科学的交叉，另外几个speaker 着重在于研究生物系统如何实现类似反向传播算法的过程。反馈的神经信号和local的Hebbian rule等的结合，可以实现类似于反向传播的修正，也就是说大家在寻找反向传播的生物基础，而且还非常有希望。

当然比较CNN不同层次的representation 和生物视神经的表示已经是老课题，目前imagenent上预训练的网络经常被用来和生物神经网络的活动比较，逐步被作为一种衡量生物神经网络表达复杂度的标尺，也是一个有意思的方法。

2，多巴胺（Dopamine）在学习回路中的作用（Ilan Witten， Princeton）

多巴胺神经元和回路是计算神经科学和强化学习的热点问题，它与我们的一切行为有关，影响我们的喜乐哀愁。 dopamine的经典理论被认为传递对未来奖励的预期信息和真实奖励的差距，这恰好对应强化学习理论的TD误差。后来人们发现这个想法太简单了。一些新的结果指出dopamine神经元作为一个数量巨大的群体，编码的信息不仅包括奖励信号，还有和奖励有关的的信号特征，比如颜色，物体的运动方向。生物系统为什么这样选择自己的强化学习算法，非常值得探讨。

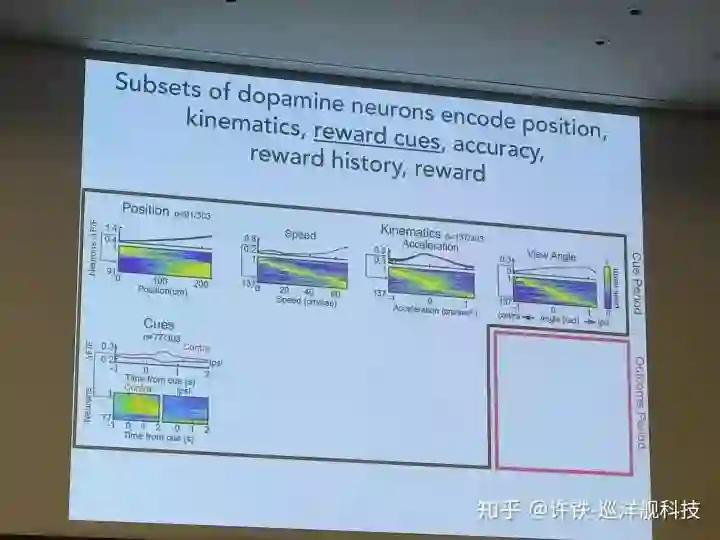
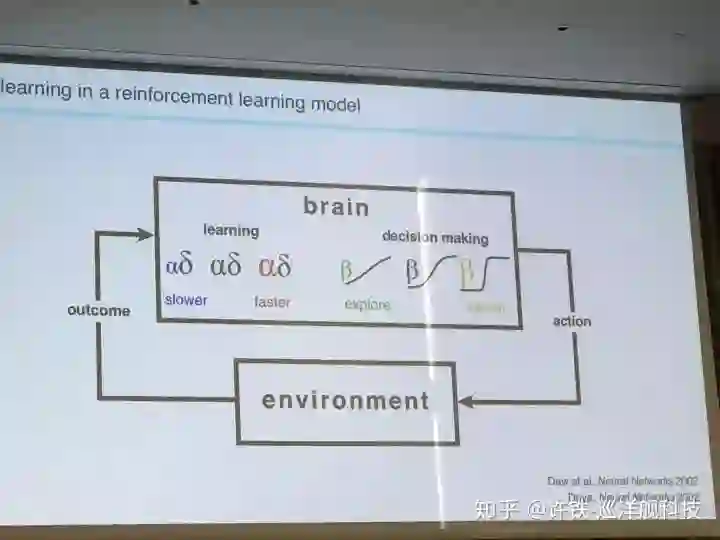
另一些工作围绕dopamine和强化学习的研究通过实验验证dopamine的数学理论，模型结合实验的方法可以很好的test这方面的idea。人们一直在争论dopamine对应value function本身还是TD误差，你能不能设计一个研究的方法很好的区分了前者和后者？事实上真实情况永远比理论模型复杂的多。

3. 神经编码的本质：高维vs低维（Kenneth Harris， UCL）

大家都知道人脑有1000亿个神经元，近似于我们说的无穷多，为什么？为什么要这么多？

神经编码的本质属性是维度，大部分时候，当我们对世界的理解抽离到最后，就只剩下维度。首先神经编码必须是高维的，这对应我们的大千世界信息是丰富的。同时我们又不希望神经编码的维度太高，我们们希望在能够表达现实世界的丰富信息的时候，这个表征流行的维度越低越好，反过来说，就是我们希望在某种限制条件下尽可能充分的表达真实世界的信息。其背后的合理性是什么？

这组实验让小鼠不停的观测从自然环境中随机抽取的图像样本（nature image），然后我们记录视皮层的神经活动，并通过PCA等降维手段来观测神经表征里的维度。首先，我们最终得到的结果是我们的生物神经网络确实具有无穷多（和图像的总数一样多）的维度（所以需要无穷多神经元表达）, 这是由于自然环境中的物体太丰富了，自然信息的维度可以是接近正无穷，这也是为什么我们的脑内需要这么多的神经细胞。

然后，我们发现并非每个维度都是均衡的，每个PC维度所刻画的信息量均匀的下降，而且这个下降呈现的衰减符合一个幂律分布。而这个幂律的数值非常关大。我们知道这个数值越小，衰减就越慢，幂律就越接近肥尾，这背后对应的是什么呢？如果我们用流型的思维看，这个指数大小正对应流行曲面的形状（你可以想象一下极限情况，如果我们只有两个PC，后面的数值均是0，我们的流型是一个平面）。越小的指数，代表高维的成分越显著，流型维度大到一定程度，就会出现分型结构（连续但不可导）。一个高维的分型结构意味着，每个样例可能都占据着一个高峰，而稍微一离开，就是波谷。

从低维流型到高维分型

这在机器学习里，恰恰意味着泛化能力很差，如果你稍微移动一下这个曲面，分类就可能变化。如果指数比较大呢？指数比较大，意味着高维成分衰减很快，这个时候，我们会得到更为平滑的流行曲面，从而得到更好的泛化能力。那么指数可不可以尽量高呢？答案是不行，因为那样导致的表征维度过低，刚刚已经说了很多遍，那样我们就失去了对丰富世界的表达能力（维度越高越好做分类，可以容纳更多互相正交的分类，模型容量高）。

总结一下这个幂律的指数值有两个关键点，当指数比较小的时候流形都是刚刚讲的分型结构，第一个关键点是从分型到平滑，而第二个关键点是神经全息成像，当衰减速度快到一定程度（低维到一定程度），我们就会得到类似全息成像的现象，此时神经信息处处是冗余，你随便找一组神经元都可以得到整个外部世界的信息。

自然界用高维冗余的非线性系统表达低维的表征，来对现实世界降维。这是神经科学和深度学习恒久不变的主题。一般情况下高维会增加分类的效率和模型的容量(正交性)，而低维则有利于泛化（平滑性，把相关类别的编码放到一起）。而在当下的深度学习里，我们恰恰缺乏这种能力，用同样的指数实验测量CNN的信息压缩特性，我们发现，它的指数衰减明显的慢于小鼠，也就是依然保留了更多高维成分，这使得它对高维信息（往往在空间上意味着高频）极为敏感。当你在已经识别很好的图像加一点噪声（高频信息）它就认错了。

这个讲话解释了很多困扰我的谜团，比如为什么需要那么多神经元，深度学习的泛化问题等等，同时把学习算法和幂律巧妙的联系在了一起。

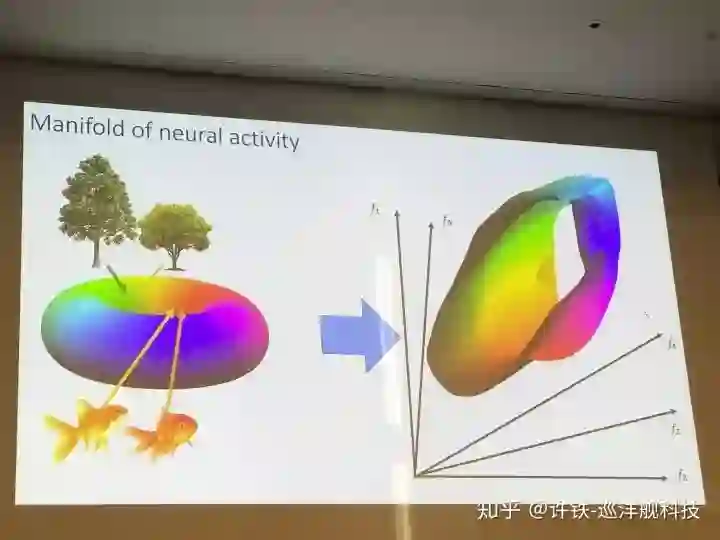
4，寻找RNN的动力学维度（Eric Shea-Brown， Univesity of Washington）

另一个研究指出用RNN解决任务时候自身动力学维度与任务维度的匹配关系。如何预测RNN所表征的系统维度？首先维度取决于背后的动力学，然后网络的动力学取决于结构，我们可以用一套启发于物理学的方法来从结构推出动力学维度。这个方法通过定位神经网络里的motif来预测其维度，可以说和费曼的场论异曲同工。

然后这个维度有什么意义？我们说这个维度与我们要执行任务本身的复杂度高度相关。如果换一个在平面上的简单分类，我们不需要实用自身动力学维度很高的系统做，而如果这个分类就是高维的，那么具有高维动力学的系统往往优于低维的。这揭示了网络动力学与真实世界动力学的内在联系。 而事实上，一般在混沌状态的网络动力学维度更高，这无形中揭示了，混沌没有看上去混乱，它可能恰恰是我们强大认知能力的基础。

5，生物导航Navigation （Edward Moser， Kavli institute, grid cell诺贝尔奖得主）

导航与空间运动相关的问题一直是计算神经科学的热点主题。 grid cell实现所谓的物体位置编码，可以把空间里的核心物体位置编码成一组向量。这种能力是如何一点点随学习和发育产生的? 这是一个非常大的主题，也是无数计算神经科学家的目标。

Navigation的一个核心主题是cognitive map 的理论。它说的是在大脑中存在一个空间表示的神经载体。你我都存在在这个认知空间里，它独立于你我而存在。根据Okeefe的理论，这个空间是hippocampus的grid cells 和place cell 作为基础提供的。 grid cell类似于一个巨大的坐标系统，而place cell 可以在每个不同的空间里重新编码（remapping）。这个十分有魅力的理论至今其实很多问题依然是悬案。

在这次的会议上， grid cell 理论的创始人Moser给了key speech，他主要描述了这种空间的神经编码应该以对空间的物体进行向量编码为基础，每个物体对应一个向量编码。同时，他讲解了提供这种空间结构的基础网络是如何从发育阶段一点点形成的。从发育阶段理解一个复杂问题通常可以把这个问题简化。

围绕这一主题的其它讲话里有几个来自以色列的研究特色鲜明。维兹曼研究所的 Alon Rubin 揭示出我们所认为的认知地图即使对应同一个环境也不仅有一个，在同一个房间运动的小鼠可以解码若干地图，这一点让我们不仅思考这些地图到底是干什么的，显然它们与不只对应我们所认识的绝对空间，因为绝对空间只有一个。

另一个来自以色列的Gily吗Ginosar 则展示了如何寻找蝙蝠头脑里的grid cell，并揭示出它符合一个三维空间的密堆积周期结构。因为蝙蝠的生活空间是三维的，所以显然它的空间表征也要是这个维度。这点让我们不禁想象，如果存在4维和5维的空间，这个表示是什么样的？到底是我们的认知确定了我们的世界，还是我们的世界决定了我们的认知？

另外一个核心问题是我们头脑里的认知地图是egocentric(自我中心) 还是allocentric（外部环境中心），所谓以自我为中心（以上下左右表达整个世界，自我就是坐标原点），还是以一个外界的坐标系（如不同的地标）为中心。经典的认知地图模型是allocentric的外部坐标表示，然而事实上很多研究指出，自我为中心可以找到很多实验证据。因此两个派别进行了激烈的辩论。

当然也有些会议上的报告讨论了place cell的真实性“它们可能仅仅是一些依照时间序列依次发放的神经集团” 来自MIT的Buffalo指出。

最后，这个方向的讨论还包含了这种能力是否能够提供空间之外的推理能力？来自马普所的教授进行了很好的开拓性发言，它认为空间的grid cell 可以作为我们的其它推理能力的一种基础形式。（更多内容参考空间简史-人类认识空间的旅程与其对强化学习的启示）

蝙蝠的三维grid cell

6 对不确定性的神经编码（Maneesh Sahani, Gatesby Unit UCL）

神经系统如何通过大量的神经元编码周边信号的不确定性是一个很重要的课题，一个有意思的主题是集群编码（population coding）。这方面的研究和机器学习里variational auto-encoder （VAE）密切相关。因为你要决策，不仅要依靠确定性的信息，还要靠不确定的信息，比如distribution。神经网络被认为具有这种编码不确定性的能力。同时这也是机器学习的核心主题，贝叶斯学习基础的神经网络-深度贝叶斯学习正在占据越来越大的研究空间。

7 贝叶斯学习(Weiji Ma, New york University)

贝叶斯学习和上面的不确定性密切相关。贝叶斯相关的模型可以迅速的建立同时包含数据和假设的模型。贝叶斯概率是非常基础的统计知识，有的人只把它当成统计，而它在神经科学的巨大潜力在于，它可以非常好的解释行为，以及大量之前模棱两可的现象。把实验数据和理论做一个极好的结合。因为通过贝叶斯方法，你可以把现有的实验数据迅速的通过似然性转化为一个预测性模型，验证你的假设。

贝叶斯模型有别其它更基础的模型，可以直接在行为上建模。你只要有先验，有似然性，就可以建立一个贝叶斯模型。比如你有两个截然不同的假设解释一种心理现象，贝叶斯方法让你直接把先验和似然性（可以通过数据检测或者直接推理得到）组合在一起解决一个问题。同时，贝叶斯方法和自编码器有很多灵活的结合，不少新的工作围绕如何在高斯假设之外实现变分自编码器。

8 强化学习

强化学习相关的主题（如果包含多巴胺）几乎占据了会议的半壁江山，这些理论可以揭示动物的行为和决策后面的大量算法基础。神经科学方面，大家围绕stratum, amygdala, basal ganglia是如何配合实现这一算法展开了大量研究。算法方面，一些研究把小鼠海马在空间导航学习中的预演“（preplay）和"回放“（replay）进行了对比。预演很像有模型学习中的计划和模拟部分，而回放可以对应到TD lambda算法的值函数回传，这些算法，都可以很好的对应到现代的深度强化学习里，但并不是每一个AI里的强化学习算法都有很好的神经对应，比如策略梯度。或许未来我们会发现两者是一致，或许不一致的部分正好可以指导我们改进AI。

最后，一个有趣的研究（David Reddish）把强化学习和神经经济学（neural economics）联系起来，让小鼠在不同的选择中权衡，我们可以很轻易的控制每个奖赏的属性（如时间，获取难度），看它怎么选择。有趣的是，从小鼠中得到的现象居然可以直接和人类进行对比。

这让我想到，目前的大量心理学理论，甚至经济学理论，可以通过强化学习，与计算神经科学和AI联系起来。

9， data inference & latent dynamics

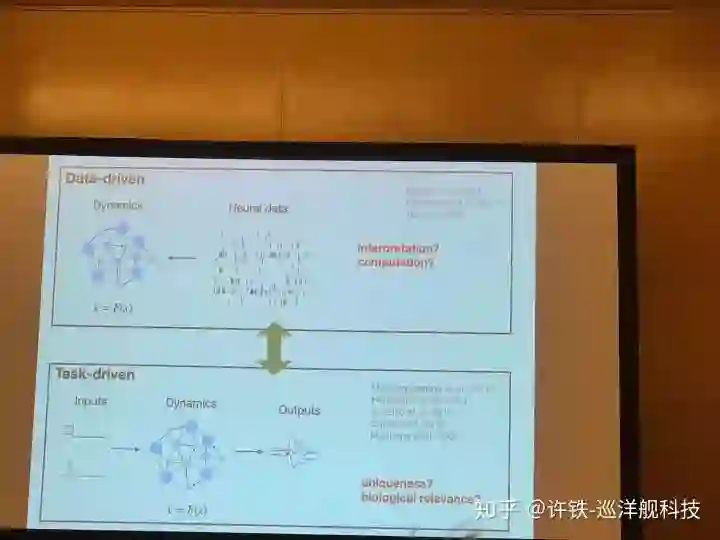
模型分成两种，一种叫做机理模型，一种叫做数据模型。所谓机理模型的核心是用第一型原理推出现象，理解现象，比如神经细胞放电的Hodykin-Hukly模型，平衡神经网络模型，这些往往是传统的计算神经科学模型。而数据现象模型，是力图用最少的参数解决复杂的现象，似乎理解了现象，然而实际只是拟合而已，但是这样的模型有时候具有泛化能力，它就是好的预测模型，几乎所有的机器学习模型都可以进入这一类。

然而对于想理解大脑的人第二类模型是不靠谱的，因为你又不是做股票，你是想理解现象。而你确实希望让第一种模型具有第二个的能力，因为如果一个机理模型可以预测现象或数据，你就更加确定它是合理的，甚至可以给出更靠谱的预测。而现在，有一些方法可以把两个模型合成成一种。其中的一大类方法基于贝叶斯推理，因为贝叶斯可以把一个”生成模型“通过贝叶斯公式，和观测数据结合起来，得到一个模型参数的后验概率，事实上相当于你用数据而不是其它的拟合了你的机理模型。然后我们可以把这个机理模型带去预测新的现象，验证它靠不靠谱。

而贝叶斯方法经常面临的问题是先验不好给出，似然性不好求解。一个更加fancy的方法是直接上机器学习里的神经网络来做参数估计。首先我们用我们”不靠谱“的机理模型通过模拟，得到大量的结果。每个模型参数，都得到一大类模拟结果。这些模拟结果和参数，就称为了神经网络的输入和labels，不过可能和你想的反过来，模拟的结果是输入，而参数是输出，这个神经网络所做的正是贝叶斯里的推测后验概率，只不过先验和似然性被包含在了模型里。由此训练好的模型，我要输入给它最终测量到的真实数据，它就会得到一组最后我想要的模型参数了。你也可以理解为它很像一个GAN的结构，机理模型在这里扮演了生成器的角色，而神经网络是一个判别器。最终生成器生成的数据要和真实数据完全一致，一个拟合就完成了。由此你就得到了最具有预测力的机理模型。

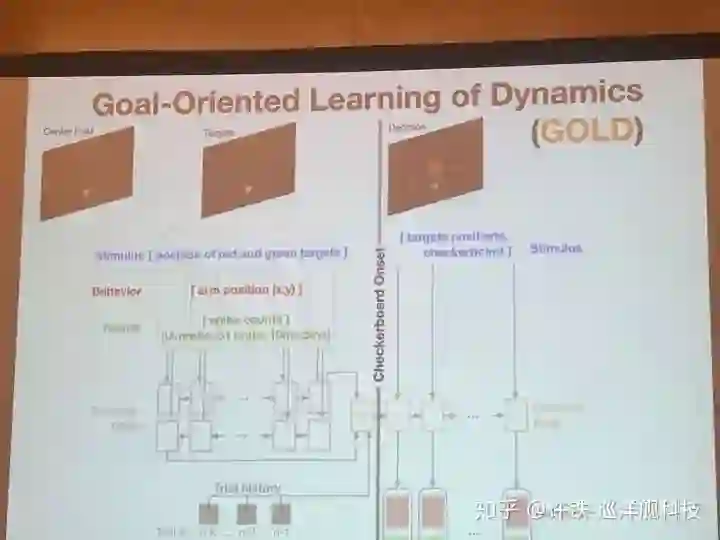
另一些讨论围绕RNN，本次会议提到了一个GOLD模型 (Daniel O'shea Stanford)。用RNN可以学习执行一个任务，比如决策，但是以往我们不知道RNN的神经元活动和真实的关系。现在，执行任务的同时我们用类似刚刚的方法让它拟合真实的实验数据（神经元活动），由此我们认为，得到的RNN就是我们脑网络的缩影，可以分析出大脑信息流动的基本原理。这类工作应该对构建大规模脑网络非常有帮助。

Gold 模型实际用到的结构类似一个自编码器，一个编码RNN把和任务有关的信息，初始条件都压缩成神经编码，而另一个解码RNN，则在所有这些信息基础上做出最后的决策，并拟合真实数据。这一类数据反推得来的模型，可以帮助我们寻找数据背后的神经活动本质，这一类认为又称为Inference of latent dynamics.

10，寻找真实神经网络模型的神经连接

一些好的计算模型，可以帮助我们找到两个真实脑网络模块之间的连接，让我们知道它们是怎么被连在一起的。这也是计算和实验非常紧密在联系在一起的一块。比如这次的会议一个talk讲了初级视皮层V1区和V2区之间的功能连接可以如何通过数据推理出来。

总结：

这次会议展示了计算神经科学的巨大魅力和潜力，以及研究的挑战。我们看到，火爆发展的机器学习的思想和方法，已经渗入了计算神经科学的所有角度，而对计算神经科学的理解，也在帮助我们制定发展通用人工智能的潜在方法。当然，计算神经科学的作用远不止这些，它和所有的心理学，认知科学，生物神经科学的关系犹如理论物理和物理的关系一样紧密。我经常惊叹某个计算理论可以如何让我们联想到一些心理现象，这个学科的发展与神经医学的联系也是不言而喻的。

然而进入这个学科的难度还是很大的，真正要在这个领域做好研究，需要精通数学里的高等代数和微积分，机器学习和深度学习的所有理论，物理里的非线性动力学和一部分统计物理知识，要求不可谓不高。

最重要的，还要有极好的思辨能力。因为这个学科不同于机器学习的是，你不是光得到一个benchmark分数很高的模型预测性能就可以了，而是要真正理解一个机理的，本质性的东西。你的模型永远来源于真实，又远远抽象于真实，如何知道你的东西不是一个toy model，而是包含了这种本质的东西？这种思辨力可能才是这个学科最有门槛的东西，也是最有魅力之处吧。

工业互联网

产业智能官 AI-CPS

加入知识星球“产业智能研究院”：先进产业OT（工艺+自动化+机器人+新能源+精益）技术和新一代信息IT技术（云计算+大数据+物联网+区块链+人工智能）深度融合，在场景中构建状态感知-实时分析-自主决策-精准执行-学习提升的机器智能认知计算系统；实现产业转型升级、DT驱动业务、价值创新创造的产业互联生态链。