会员服务 ·

财运和桃花运的数学配方

2018 年 11 月 26 日 行业研究报告

提示：点击上方"行业研究报告"，关注本号。

行研君说

导语

“生活的不确定性正是我们希望的来源。”——阿尔弗雷德·阿德勒

PS：我们运营的备用号行研资本（ID：report18）为很多老朋友提供了另一处空间，欢迎大家同时关注！

来源：老喻在加孤独大脑（ID：lonelybrain）

运气是靠设计，

还是设计的残余物质？

运气可以设计吗？

众所周知，运气的特点就是不确定性，无法预测，难以把握。如果运气可以设计，那还叫运气吗？

但有个人说可以。他在给儿子的信中说：

运气靠策划。

在那封信的开始，他提及了老麦考密克先生，说该人长着一颗能制造运气的脑袋，知道如何将收割机变成收割钞票的镰刀，他用收割机解放了美国农民，同时也把自己送入全美最富有者的行列。

老麦考密克先生说过一句深奥的名言：“运气是设计的残余物质。”

这句话听起来的确让人颇费脑筋，它是指运气是策划和策略的结果，还是指运气是策划之后剩余的东西呢？

我的经验告诉我，这两种意义都存在，换句话说，我们创造自己的运气，我们任何行动都不可能把运气完全消除，运气是策划过程中难以摆脱的福音。

写信的人是约翰·戴维森·洛克菲勒，1870年创立标准石油，1914年巅峰时，其财富总值达到美国GDP的2.4%(9亿美元，美国GDP365亿美元)，折合今日值4000亿美元以上，被视为西方世界史上首富。

神秘的运气，

不可言说。

特别幸运的人，和特别不幸的人，都显得很相信命运。

运气好的人，在发表获胜感言的时候，都是先赞美运气。

例如美团的王兴在公司上市时，感谢乔布斯开创的智能手机时代，盖茨总是强调我们很幸运，出生在人类有史以来最好的时代；巴菲特则说自己中了子宫彩票。

运气不好的人，哀叹自己喝杯水都塞牙缝，感觉全世界都和自己对着干，身边每个人都是敌人派来的，好运气来到手边都不相信是真的，拿到手上都要往地上摔一下加以验证：你看，我说的吧，假的运气！

运气是如此重要，人们对运气如此迷恋，运气又是那么不可言说。

我们看到的运气方面的解释，要么陷入社会学的陈词滥调，要么陷入用数学和物理来为伪科学胡说八道。

由此倒是催生了庞大的“运气产业”。包括：风水、星相、（某些）心理学、成功学，旺夫班。

还有很多人，自己本来就是运气的“偶然样本”，作为“幸存者偏差”，到处去传播“偏见”。

以此开篇冒着巨大的风险，一方面我表现出雄心壮志，另一方面如果我以下的思考“不甚了了”，你不妨把本文也扔进上面的筐里。

一碗鸡汤，

幸运的配方。

Dr. Richard Wiseman写过一本叫《幸运的配方》的书，来分析幸运和超能力到底有没有关系。我从不相信超能力，作者既然觉得这个还值得讨论，他给出的配方也是比较鸡汤、但尚可入口的：

配方一：运气好的人会创造、注意机会，并在好运来临时采行动。

作者提及三种性格：

a、外向。更多朋友，更多机会；

b、情绪紧张。Wiseman做了个实验，约轻松型和焦虑型的人去咖啡馆访谈，结果轻松的人更容易发现故意放在地上的钞票；

c、开放度。别局限自己，不限制自己，就会发现更多机会。

配方二：靠直觉和第六感作出“成功”的决定。

这一点不赞成不反对不评论。但是作者举的某个例子还可以，说是遭遇过烂人的女性们，起初大多有不太好的感觉，但又说服自己是不是想太多了，结果就是不好。

这是不是“事后归因”姑且不说，但别把感觉不爽的人纳入“核心圈”，这个我也深有同感。但是按照配方一，你又要有“开放度”，这咋办呀？

鸡汤从来不对自相矛盾负责。

配方三：就是相信自己有好运，心安理得地期待着。

相信自己有好运的人，容易相信别人是好人，就容易遇到好人，或者唤醒别人潜意识里的“好人”，对他表现得比较好；

认为自己倒霉的人，对身边的人充满了怀疑，令人厌倦，结果终至“一语成谶”。

此乃“皮格马利翁效应”。

配方四：将厄运转为好运。

丢了十块钱，安慰自己幸好丢的不是一百块。将好事或者坏事视为机会的“触发点”。

成功与运气，

随机和感恩。

在另外一本更加高大上的《成功与运气》一书中，罗伯特·弗兰克总结了运气的三条规律：

规律一，运气是可以放大的。

越是人生早期的关键节点，运气的放大作用越明显。加拿大青少年冰球运动员选拔系统在每年 12月 31日这天给年龄划线， 1月出生的球员就比 12月出生的更有可能获得那份年薪 3 100万美元的职业合同。

这个原理反过来，也正在摧残着中国的孩子和家长们。为了赢在起跑线上，升入名校，人们不断向前“偷跑”。

结果，大家就像站着看电影，所有的人都踮起脚来看，都累，都占不到便宜，运气的放大，也就无从谈起了。

规律二，运气是可以累加的。

比尔·盖茨当然有天赋也有努力，可是他如果不是正好出生在个人电脑第一波浪潮时代，正好进入全美唯一一所允许学生无限制访问具有“及时反馈”功能的计算机终端的私立学校，以及后面的一系列“正好”，个人电脑的主宰公司就不会叫“微软”。

这个话题正好呼应了乔布斯那个著名的演讲，你要主动地将人生的某些事情串起来，就像你怎么知道你的手机上好看的字体，来自一个嬉皮士大学生的一门字体设计旁听课。

规律三，竞争越激烈，运气越重要。

我们今天面对的市场是一个赢家通吃的市场。水平相当的两个人，运气上的差距若为 5%，收入上的差距可能高达 500%；同一类型的两个产品，性价比上的差距若为 5%，则可能直接导致差的那种被淘汰。

该书核心主题是，那些看似微小的随机事件对我们生活的影响，远远超出了大多数人的想象。

研究结果显示，感恩能带来很多好处。它会让人们更快乐，更健康，拥有更好的人际关系，进而收获更多的尊重。

所谓感恩，就是运气好的时候感谢运气如此厚待，运气不好的时候感谢运气不杀之恩。

双罐模型，

实力与运气的计算。

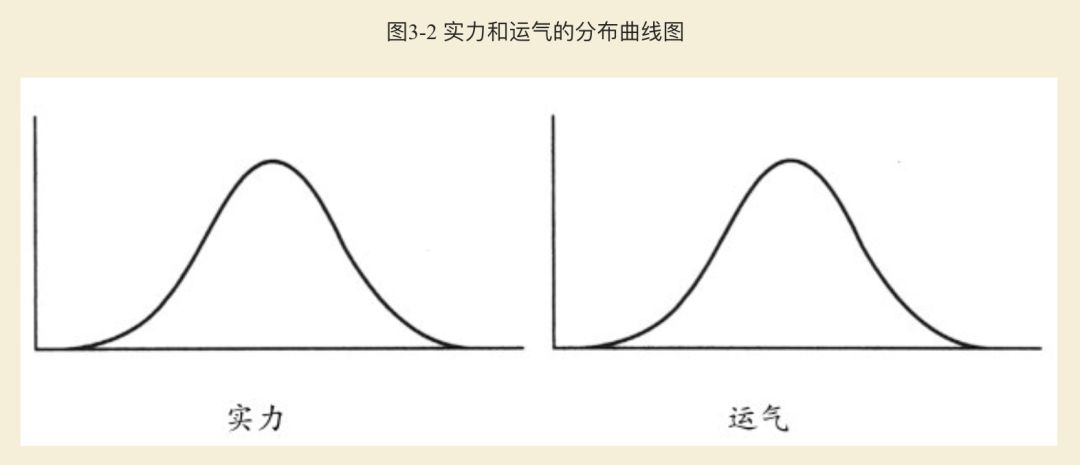
《成功与运气》一书，给出了运气的测算方法：双罐模型。

假设你有两个罐子，里面装满了小球，每个小球都有数字标号。一个罐子中的小球代表实力，另一个罐子中的代表运气，球上的数字越大越好。

然后你从两个罐子中分别取出一个球，将球上的数字相加。

下图显示的是，两个小球之和正好呈钟形曲线分布。这个模型能有助于我们更好地理解事件的本质。

赢家通常都是因为两个罐子里的球都是最大数字。

葛拉威尔说，无数的成功故事告诉我们“人群中的异类之所以能够到达成功的金字塔，靠的不仅仅是实力，更是机遇和完全随机的有利条件”。

这正是双罐模型所揭示的道理。两个罐子里都是最大数。

当游戏被不断重复，运气那部分会逐渐稳定下来。

这只是一个简单化的模型。两个罐子并非是对称的。比如看看是不是有回归现象，回归越明显，说明运气作用更大。保尔森的业绩回归，说明投资领域“运气”很重要。

以上5节，都是从偏文的角度来谈“运气”，下面试一下偏理。

我们顺着双罐模型，往数学里稍微走远一点儿，里面还有一点点儿力学的东西。

概率模型，

运气降临+你的反馈。

运气的最大特点，是不确定性。

而概率模型是对不确定现象的数学描述。

如前所述，运气本质上等于“运气降临+你的反馈”。

运气是不确定性的，与概率相关；
而你的反馈，也是在条件不充分的情况下作出的，所以，几乎每一个你有意识地作出的决定都与概率相关。

概率，旧称几率，又称机率、机会率或或然率，是数学概率论的基本概念，是一个在0到1之间的实数，是对随机事件发生之可能性的度量。

概率常用来量化对于某些不确定命题的想法，命题一般会是以下的形式：“某个特定事件会发生吗？”，对应的想法则是：“我们可以多确定这个事件会发生？”。

确定的程度可以用0到1之间的数值来表示，这个数值就是概率。因此若事件发生的概率越高，表示我们越认为这个事件可能发生。

像丢铜板就是一个简单的例子，正面朝上及背面朝上的两种结果看来概率相同，每个的概率都是1/2，也就是正面朝上及背面朝上的概率各有50%。

这些概念可以形成概率论中的数学公理（参考概率公理），在像数学、统计学、金融、博弈论、科学（特别是物理）、人工智能/机器学习、计算机科学及哲学等学科中都会用到。

概率论也可以描述复杂系统中的内在机制及规律性。

（以上来自维基百科）

概率好玩儿的地方是，一方面它是如此强大，另一方面是我们只需了解最基本的两个基本概念，就足以应付这个现实世界了。

先来点儿概率常识：

第一个基本概念：相互排斥事件

如果两个事件不可能同时发生，则这两个事件就是排斥事件。

例如上图的转盘游戏，指针落在红色或者紫色上，这两件事就是排斥的，你转动一次，不可能同时落在两种颜色上（不考虑临界点）。

如果事件A和B是排斥的，那么“事件A或B发生”的概率就是A发生概率和B发生的概率相加。

在上图中，落在红色上的概率是1/5，落在紫色上的概率是1/5，所以落在红色或者紫色上的概率就是2/5。

第二个基本概念：相互独立事件

相互独立事件: 事件A（或B）是否发生对事件B（A）发生的概率没有影响，这样的两个事件叫做相互独立事件。

严格来说，如果两个事件A和B同时发生的概率等于A发生的概率和B发生的概率的乘积，则这两个事件是独立事件。

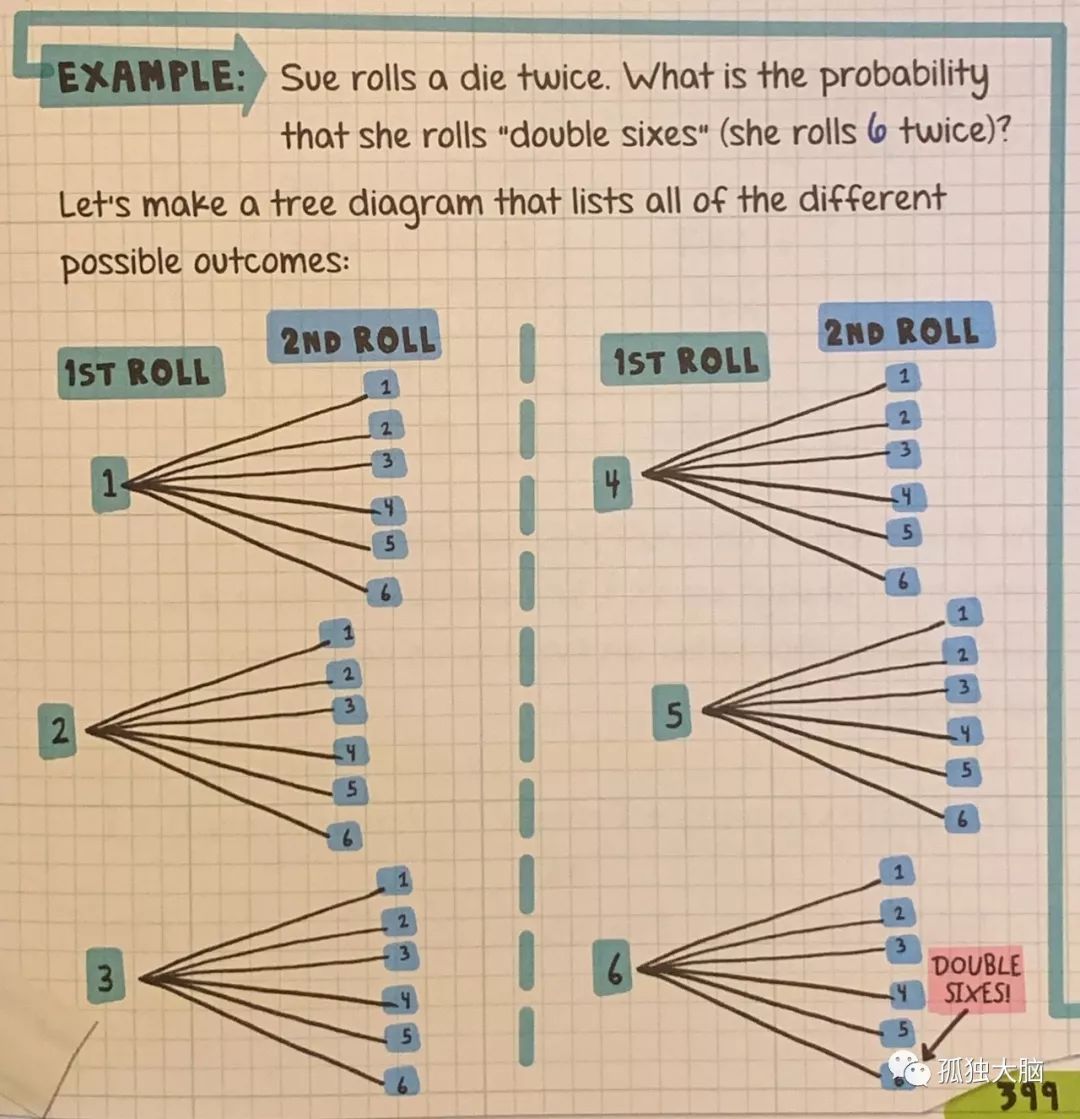
如上图，常见的扔骰子游戏：如果你连续扔两次骰子，你有多大概率连续得到两个六？

上面的解答，是我从加拿大这边的一本中学数学辅导书里拿来的。这是一种“穷尽法”，也就是说，把所有可能发生的情况全部罗列出来，既直观又清晰，有利于我们理解概念的本质，如果仅仅记一下公式，其实毫无意义。

我们看到，绿色是指第一次扔骰子时，会有六种可能性。那么，对应第一次的每一种可能性，第二次扔骰子又分别有六次可能性，即蓝色的部分。
算下来，一共有36种可能性，两个全是6的可能性是1次，所以是1/36。
用公式来表达，就是1/6*1/6=1/36。

有人可能会说，天哪，你是在帮我复习中学数学吗？

事实情况是，就是这么简单的两个基本概念，现实生活中能够弄明白的，也许只有1/1000；能够以此作为决策依据的，更是万里挑一。

否则，谷歌就不会出下面这道题来挑选“天才”员工了，如下：

谷歌面试题——汽车经过的概率：

假设在一段高速公路上，30分钟之内见到汽车经过的概率是0.95。

那么，在10分钟内见到汽车经过的概率是多少？

这道题看起来简单，想明白不容易。最后做起来，又只需要上面两个最基本的概念即可。

（为了避免让本文有太多计算，这里不做解答。想知道答案？请在公众号对话框回复：汽车）

控制运气的运气，

从执行层到配置层。

拉普拉斯说：概率是用计算概括的常识。

让我们回到我在《混合算法》里提及的案例：

泰德•威廉姆斯在他的《击球的科学》一书中这样描述道：对于一个攻击手来说最重要的事情就是等待最佳时机的出现。

巴菲特认为这句话准确道出了他投资的哲学，等待最佳时机，等待最划算的生意，它一定会出现，这对投资来说很关键。

泰德•威廉姆斯是过去70年来唯一一个单个赛季打出400次安打的棒球运动员。他的技巧如下：

第一步：把击打区划分为77个棒球那么大的格子。

第二步：给格子打分儿。

第三步：只有当球落在他的最佳“格子”时，他才会挥棒，即使他有可能因此而三振出局，因为挥棒去打那些“最差”格子会大大降低他的成功率。

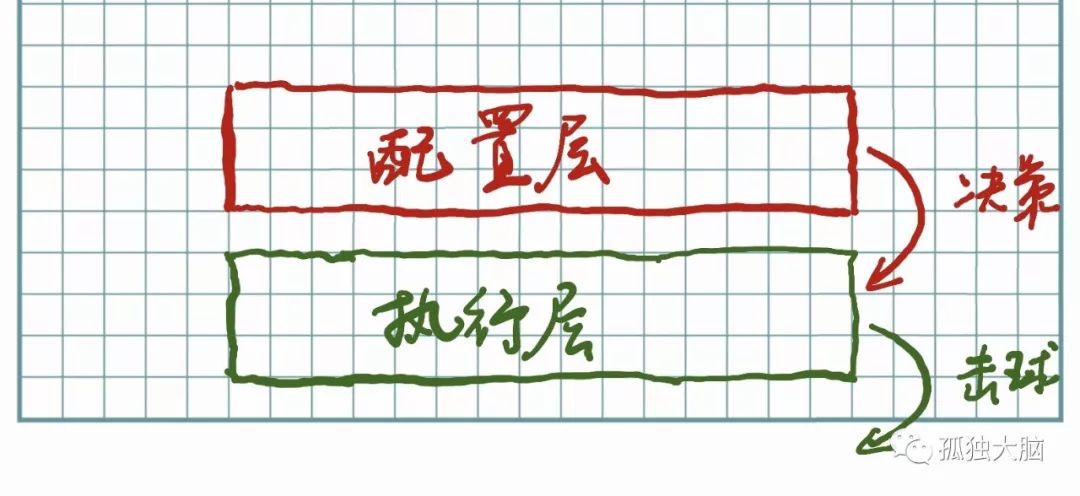
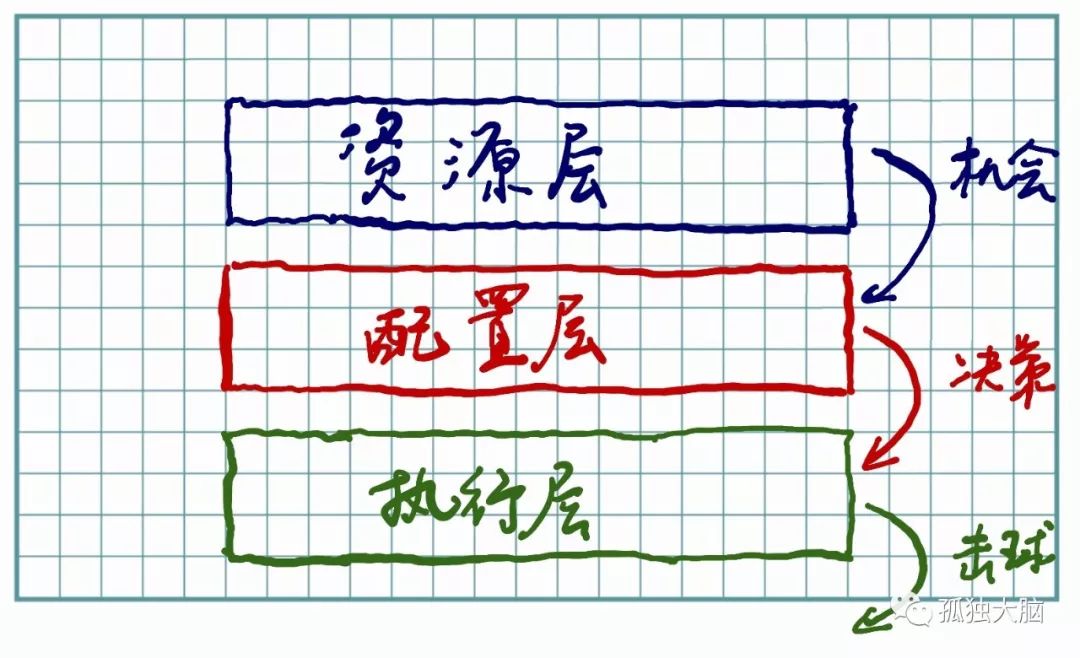
如上图，泰德•威廉姆斯的秘密在于，将自己的“概率世界”变成了两层。

一层是执行层：也就是他击球这个层面。

在这个层面，无论他多么有天赋，多么苦练，他的击球成功概率达到一定数值之后，就基本稳定下来了，再想提升一点点，都要付出巨大的努力。而且还要面临新人的不断挑战。

一层是配置层：也就是他做选择的这个层面。

他在配置什么呢？

挥棒击球的决心。

让我们继续用概率模型来分析。

如上图：

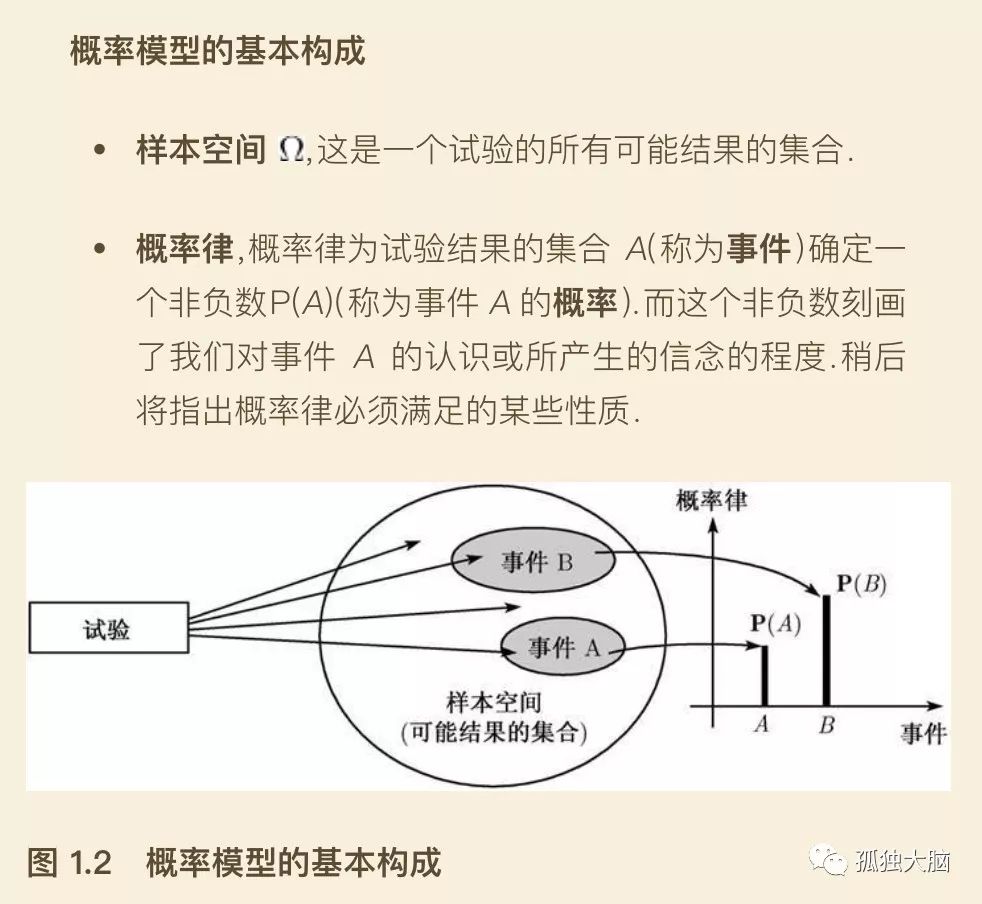
a、“试验”可以视为对手，他是所有飞来的球的“发生器”；

b、“样本空间”里，包含了所有飞来的球，事件A就是球A，事件B就是球B；

c、“概率律”，在这个特定的隐喻里，我们是指A类球飞来的时候，假如泰德•威廉姆斯挥棒的话，他的成功率。

（请注意，这里面有两个需要用概率来描述的指标，一个是飞来的球，一个是击球成功率，在此我简化了。）

如上图，假如所有的球只有A和B两种，A的成功概率较低，B的成功概率较高。

所以，在“样本空间”这个环节，我们可以对事件进行筛选：

当事件A发生时，我们什么都不做；
当事件B发生时，我们全神贯注地挥棒击球。

我们悄悄地将此前的双罐模型，变成了双层模型：

我们把原来的“运气罐子”，变成了配置层。“实力罐子”，称之为“执行层”。

如此一来，我们发现，伟大的球员是由杰出的决策能力（设计自己的运气）和强大的运动实力（实现自己的运气）共同造就的。

的确，我们并非完全被运气所操纵。

很多时候，我们无法改变运气，但可以改变运气的运气。

红色球蓝色球，

对随机性的配置。

配置层只是“对坏球说不”吗？

远远不是。

为了论证这一点，我们来看一道有趣的微软面试题：

微软面试题——两个罐子：

有100个红色球和100个蓝色球，请你任选组合将全部球放入2个罐中。放好后随机取一个罐子，再从此罐中随机取出一个球，如果取到红球赢100元钱，问如何组合放球能最大化赢钱机会？

看起来拿到红球的概率只有50%，在配置层你又不能对蓝球说不，该怎么办呢？

答案是：

在一个罐子里面只放一个红球，而把其它所有球全部放进另外一个。

解题思路：

这里面的秘密是罐子的随机性和球的随机性。每个罐子都有50%的被选可能性。
所以干脆令其中的一个罐子最大化，全部放红球，放一个就够了。
其它99个红球放去另外一个罐子，和100个蓝球“战斗”。
这样的话，你赚钱的概率是74.87%，远高于表面上应得的50%。

稍微跳跃一点儿，我们还可以想起田忌赛马，或者下面这个段子：

三层模型，

好运气的三个旋钮。

让我们回头，将开篇所提的运气的其它因素也放进来，包括机会，开放度，人脉等等，如此一来，我们得到一个“三层模型”：

如此以来，各路学家乱七八糟的理论和建议，就有了一个（看起来）清晰的架构了，而且，为概率分析搭建了可计算的框架。

第一层关键词：获取资源，讲故事，为自己制造运势，正向的马太效应，保持开放性，交友的“开放度”，等等。

第二层关键词：分配资源，理性，远见，计算，在球将要去的地方。两个字：将，要。本质上，也是分配概率。

第三层关键词：做一个职业化的执行者，发挥个人独特优势。只要稳定在某个水准即可。例如你有52%的胜率，你稳稳地去实现即可。不管好坏，打出去，只管自己的正常发挥，以及不断提升。赢了开心，死了认命。

以我们开篇到此半句都没说的桃花运为例吧：

1、资源层

你要多交朋友，扩大交际圈，增加样本量，保持潜在对象的多样性与丰富度。

2、配置层

别见一个就All in，这哪里是相信缘分相信爱情，压根儿就是和概率对着干。在足够的样本量（不是鼓励花心哈，从普通朋友开始）基础上，作出相对理性的、尽量正确的决策。

3、执行层

这时候就是你大显身手、发光放电、死缠烂打的时候了。

有了这个框架，你会发现，桃花运的难题，90%出现在“三层模型”的战略层面，而非“击球”的技术环节。

例如：

圈子太小，样本量匮乏；
混淆资源层和配置层，爱一次伤一次；
该出手时含蓄扭捏。

简而言之，运气由三层构建，好运气取决于三个旋钮。最终结果决定于三层的整体完成度，而不是某一层的强大。

但是三层模型又不是一个简单的叠加的、递进的关系，它还有系统动力学的反馈、自我强化等特点。

例如执行层较强，可以带来更多资源。

以上三层，又都在一个巨大的运气之船上。因为我们在每一层的计算，都难免有些主观，有所偏差。

三层模型，

好运气的三个旋钮。

回到开始的那封信。洛克菲勒给儿子写道：

在我们这个世界上，很难找到像麦考密克先生那样善于策划运气的人，也很难找到不相信运气的人，和不误解运气的人。

在凡夫俗子眼里，运气永远是与生俱来的，只要发现有人在职务上得升迁、在商海中势如破竹，或在某一领域取得成功，他们就会很随便、甚至用轻蔑的口气说：“这个人的运气真好，是好运帮了他！”这种人永远不能窥见一个让自己赖以成功的伟大真理：

每个人都是他自己命运的设计师和建筑师。

洛克菲勒用自己的亲身经历来阐释他的“伟大真理”：对石油产业的整合，以及最终实现垄断。

背景：炼油商们各自为战，绝大多数都亏本。

机会：驯服这个行业，让大家理性行事。

计划：将大本营科利佛兰作为发动统治石油工业战争的第一战场，待征服在那里的二十几家竞争对手之后，再迅速行动，开辟第二战场，直至将那些对手全部征服，建立石油业和新秩序。

难题：没钱。

解决：组建股份公司，把行业外的投资者拉进来。

开局：企业就如战场，战略目标的意义就是要造成对己方最有利的状态。出于战略上考虑，选择的第一个征服目标不是不堪一击的小公司，而是最强劲的对手克拉克-佩恩公司。

进攻：接下来，二十二家竞争对手归于标准石油公司的麾下。

结局：在此后三年时间里，连续征服了费城、匹兹堡、巴尔的摩的炼油商，成为了全美炼油业的惟一主人。

如何策划运气呢？洛克菲勒就认为，在构思好的设计时，要首先考虑两个基本的先决条件：

第一个条件：知道自己的目标，譬如你要做什么，甚至你要成为什么样的人；

第二个条件：知道自己拥有什么资源，譬如地位、金钱、人际关系，乃至能力。

这个案例好玩儿的地方在于，一场资源领域的商战，最后起到决定性作用的，竟然不是资源本身的优势。

回到我们的“三层理论”框架，洛克菲勒在“资源层”没有领先对手的地方，在“专业层”也谈不上有什么“别人赚不到钱但我能”的独到之处。

他唯一有优势的是第二层。

洛克菲勒如此揭示他的秘密：

你可能先有一个构想、一个目标，才开始寻找适于这些资源的目标。

还可以把它们混合一处，形成第三和第四种方法，例如拥有某种目标和某种资源，为实现目标，你必须选择性地创造一些资源，也可能拥有一些资源和某个目标，你必须根据这些资源，提高或降低目标。

你根据资源调整目标或根据目标调整资源之后，就有了一个基础——可以据以构思设计的结构，剩下的东西就是用手段与时间去填充，和等待运气的来临了。

在洛克菲勒看来：设计运气，就是设计人生。

最后

洛克菲勒给我们四点启示：

1、大多数石油商只是把自己当作一个球手，而他着眼全局。

他能从更高维度去洞察整个行业，发现机会，并从“资源层”和“配置层”发力，最终令“执行层”（炼油业务）本身能够赚钱。

2、即使是资源行业，核心优势也不是靠资源本身。

地产行业看起来也主要靠土地，但是中国领先的几家开发商，起初都没什么土地资源优势。

丝绸之路，远比丝绸更有价值。

互联网行业更不消说了。

所以，别用“没资源”当作运气不好的借口。

3、只有数字作数。

洛克菲勒遵循母亲的教导，勤快、节俭、朴实，幼年的他已开始以帮父母做家事，卖马铃薯，火鸡，甚至贷款给邻居收息等方法赚钱。

学生时代，他喜欢并擅长于算术，但别科成绩平平。他并不属于才华洋溢耀眼型的人物，但永远严格系统化，理性不带感情地处理问题。

设计运气，就是对不确定性的计算，越难以计算，该其计算也越有价值。

4、为运气感恩。

谈及慈善，巴菲特和盖茨都是洛克菲勒的追随者。洛克菲勒回报地球的善举不胜枚举，其中最大的海外项目是中国的协和医院，累计捐助数额达4465万美元，相当于今天的近10亿美元。

鲜为人知的是，周口店“北京人”的挖掘和考古工作，洛克菲勒基金会从一开始就参与其中。

洛克菲勒在86岁时，写下一首短诗总结自己的一生：

我从小就被教导既要娱乐也要工作，

我的人生就是一个悠长，愉快的假期；

全力工作，尽情玩乐，

我在旅途上放下了一切忧愁，

而上帝每天都善待着我。

——END——

【PS：点击以下图片可查看内容】

【 投资&学习 】

课程	地点	价格	查看
私募类	北大中关新园	2.98万/年	详情
管理类	清华大学	2.98万/年	详情
上市类	社科院研究生院	8.8万/年	详情