RBS: 最优时间复杂度的single-target PPR算法 | 作者带你读论文（KDD2020）

论文题目： Personalized PageRank to a Target Node, Revisited
论文作者：Hanzhi Wang, Zhewei Wei, Junhao Gan, Sibo Wang, Zengfeng Huang
论文通讯作者：Zhewei Wei (魏哲巍，中国人民大学教授)

解读文章作者：王涵之
 
前言：Personalized PageRank（简称 PPR）是一种图节点邻近度的度量方法，被广泛应用于图挖掘和网络分析等领域。本篇论文关注 single-target PPR（单宿 PPR）的计算问题，提出了一种高效计算单宿 PPR 的算法 RBS，改进了单宿 PPR 计算的时间复杂度。当以相对误差进行结果约束时，RBS 首次将单宿 PPR 问题的计算复杂度降低至理论下界，即达到了最优计算复杂度。同时，单宿 PPR 的广泛应用也使得 RBS 算法可以进一步改进这些应用问题的运行效率，如频繁命中节点的查询问题（heavy hitters PPR query）、单源 SimRank 的计算问题、图嵌入和图神经网络中的 PPR 矩阵计算问题等。

1. PageRank和Personalized PageRank：

PageRank 最早由 Google 创始人 Larry Page 和 Sergey Brin 在 1998 年提出，用于度量 web 网络中各网页的重要性，其核心思想为：被很多网页所链接的网页重要性较高；被重要的网页所链接的网页重要性较高。如果我们将 web 网络转化为图结构G=（V，E），将 web 网络中的网页看作图结构中的节点，将网页间的链接关系转化为图结构中的连边（如果网页 A 有一条指向网页 B 的链接，图结构 G 上对应有一条从节点 A 指向节点 B 的边），则可对应写出 PageRank 的定义式：

 

2. 问题定义：

在本篇论文中，我们重点关注单宿 PPR（single-target PPR）的计算问题，即给定图上某一节点t作为宿点，计算节点 t 关于图上所有节点的 PPR。单宿 PPR（single-target PPR）和单源 PPR（single-source PPR）相对应，提供了 PPR 重要性的两种考量方式。单源 PPR 希望计算图上所有节点相对给定源节点 s 的 PPR，即希望找到所有相对源节点较为重要的节点；而单宿 PPR 则希望找到相对图上任意节点，使宿节点的重要性较高的节点。

综上所述，如果可以改进单宿 PPR 的计算效率，则可进一步提高这些问题的计算速度。

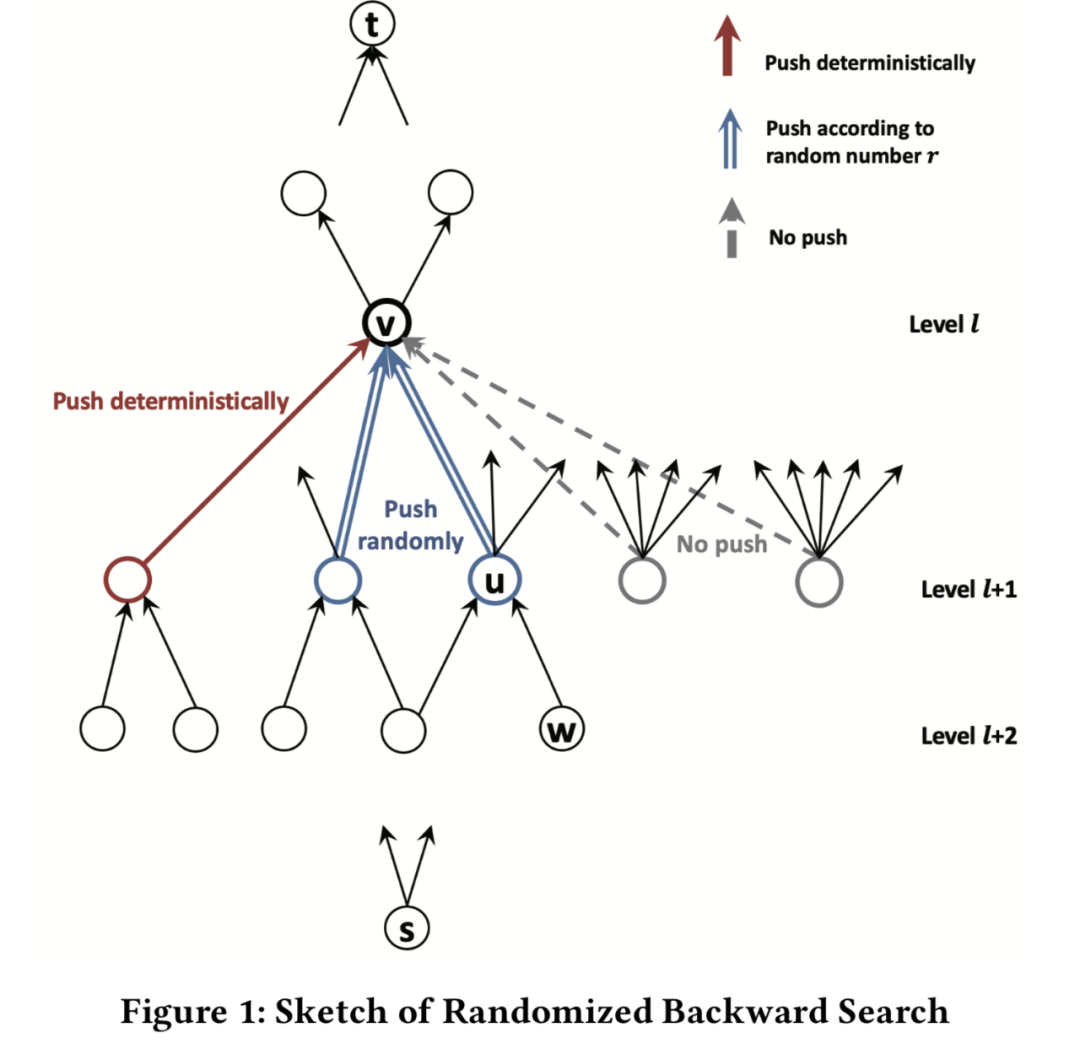
3. RBS算法：

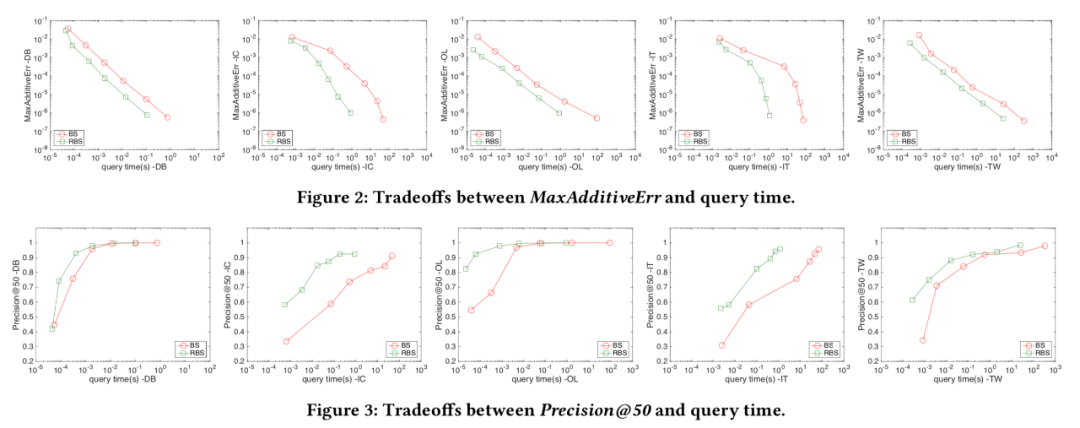
4. 实验评估： 

点击 阅读原文 ，查看更多精彩！

喜欢本篇内容，请 分享、点赞、在看