定量描述估计误差,让你离最优投资组合更近一步
一个案例说明优化模型面临的问题
source:萝卜投资
source:萝卜投资
萝卜投资对优化模型的改进
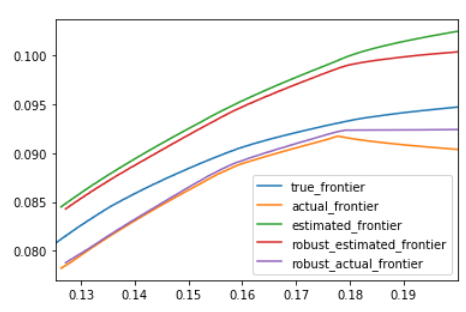
source:萝卜投资


登录查看更多
相关内容
Arxiv
4+阅读 · 2018年5月15日
一个案例说明优化模型面临的问题
source:萝卜投资
source:萝卜投资
萝卜投资对优化模型的改进
source:萝卜投资