AI「王道」逻辑编程的复兴？清华提出神经逻辑机，已入选ICLR

选自 arXiv

作者：Honghua Dong 等

机器之心编译

深度神经网路一直被人诟病的地方在于，缺少逻辑推理能力，它只是一种函数拟合方法。在这篇论文中，清华、谷歌和字节跳动的研究者提出了一种名为神经逻辑机的模型，它可同时用于归纳学习与逻辑推理。它结合神经网络与逻辑程序设计（逻辑编程），让神经网络也能用于逻辑推理。

这篇论文被接受为 ICLR 2019 的 Poster，它的评分为 6、5、7。正如评审该论文的领域主席所言，这篇论文提出了一个非常有意思的正向链模型，它利用了元层级的扩展，并以一种非常简洁的方式降低了谓项参数，从而降低了复杂度。

• 论文链接：https://arxiv.org/abs/1904.11694

• 演示地址：https://sites.google.com/view/neural-logic-machines

在该论文的展示页中，作者们也介绍了各种任务的效果，包括排序、最短路径搜索和积木世界等。其中所有智能体都通过强化学习训练，智能体会根据当前状态迭代地选择动作，直到一个 Episode 结束。

下面我们简要展示神经逻辑机（NLM）在最短路径搜索和积木世界上的表现。

1. 最短路径搜索

该任务会随机生成一个无向图，智能体需要从开始节点一步步走到目标结点。例如如果我们将初始结点定义为 s、目标结点定义为 t，那么 s 到 t 之间的距离为 d，d 是从区间 [1, 5] 中均匀采样的。

结果是，NLM 智能体能搜索到最短路径。

2. 积木世界

该任务有两个世界，即操作世界（operating world）和目标世界，下面视频分别展示在上面和下面两部分。每一个世界包含 n 个积木，该任务的目标，即采取一系列动作将初始的操作世界转换为目标世界。

结果是，智能体能搜索到正确的积木移动顺序，并将初始状态转化为目标状态。

什么是「学习」解决不了的

机器学习已经成功应用在语音识别、游戏等诸多领域，但联结主义模型的系统性（systematicity）问题仍然存在争议。

逻辑系统可以自然地处理语言理解和推理中的符号规则。归纳逻辑程序设计（ILP）从例子中学习逻辑规则。粗略地说，给定一组正负样本，ILP 系统可以学习一组规则（带有不确定性），其中包含所有正样本，而不含负样本。将符号和概率结合起来，可以很自然地解决许多高级认知能力（如系统性）带来的问题。然而，由于组合规则（compositional rule）的搜索空间巨大，ILP 很难扩展到小型规则集合之外。

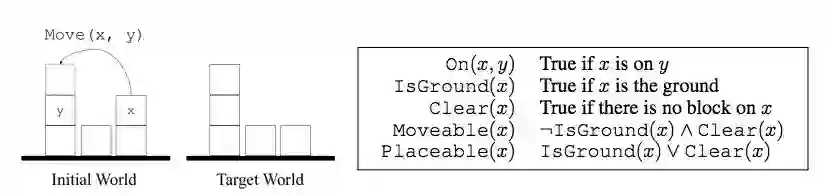
为了更加具体地讨论，该研究以经典的积木世界（blocks world）问题为例。如图 1 所示，给定一堆积木，我们可以移动一块积木 x 并将其放在另一块积木 y 的上方或地上，前提是 x 可以移动并且 y 上可以放积木。我们将这种操作称之为 Move(x, y)。如果一块积木上没有其他的积木，那么这块积木就是可以移动的，而且上面可以放其他积木。地上一直可以放积木，也就是说我们可以把所有积木都放在地上。给定积木世界的初始状态之后，我们的目标就是通过一系列移动操作将其转换为目标状态。

图 1：（左）积木世界图示。给出原始和目标状态，要求智能体通过移动积木将原始状态转换为目标状态。（右）本文用到的积木世界术语。

虽然积木世界问题乍看之下非常简单，但构建学习系统来自动完成此任务存在四大挑战：

1. 学习系统应该恢复一套已经解除的规则（即那些统一应用于对象而不是与特定对象绑定的规则），并泛化到比训练中积木数量更多的积木世界中。为了对此有一个直观的认识，此处向不熟悉积木世界的读者推荐数组排序任务（如 Vinyals et al., 2015），在这个任务中，循环神经网络无法泛化至比训练数组稍长的数组。

2. 学习系统应该处理高阶关系数据和量词（quantifier），但这超出了常见图结构神经网络的范围。例如，为了应用关系 r 的传递律（即 r(a, c) ← ∃b r(a, b) ∧ r(b, c)），我们需要同时检查三个对象（a, b, c）。

3. 学习系统应该扩展规则的复杂性。现有的逻辑驱动方法（如传统的 ILP 方法）计算复杂度为指数级，即需要学习的逻辑规则数量巨大。

4. 学习系统应该基于最小的学习先验集恢复规则。相比之下，传统的 ILP 方法通常需要手工编码和针对特定任务的规则模板，来限制搜索空间大小。

为什么结合逻辑编程的学习方法能 Work

在这篇论文中，研究者提出了一种名为神经逻辑机（Neural Logic Machines，NLM）的算法，它可以解决上面学习方法解决不了的问题。简而言之，NLM 提供了一种神经符号（neural-symbolic）架构，它以一阶逻辑实现 Horn clauses (Horn, 1951)。NLM 的关键思想即神经网络可以高效地逼近逻辑运算，例如 AND 和 OR 等运算逻辑，且神经模块之间的连接可以实现逻辑量词。

论文：NEURAL LOGIC MACHINES

摘要：该研究提出了一种神经-符号架构——神经逻辑机（NLM），该架构可用于归纳学习和逻辑推理。NLM 利用神经网络（作为函数逼近器）和逻辑程序设计（作为符号处理器），处理具备不同属性、关系、逻辑联结词（logic connective）和量词的对象。在小规模任务（如对短数组排序）上进行训练后，NLM 可以恢复一些已经被取消的规则，并泛化至大规模任务中（比如对较长数组进行排序）。实验证明，NLM 可在大量任务中获取完美的泛化效果，包括对家族树和通用图进行关系推理的任务、决策任务（包括数组排序、寻找最短路径、积木世界）等。大多数任务对于神经网络或归纳逻辑程序设计自身是很难完成的。

神经逻辑机（NLM）

NLM 是逻辑机在封闭世界假定下的神经网络实现。给出一组基于 object（前提）的谓项，NLM 序列地应用一阶规则（first-order rule）得出结论，如某个 object 的属性。举例来说，在积木世界任务中，基于 object u 的前提 IsGround(u) 和 Clear(u)，NLM 可以推断出 u 是否可移动。

NLM 内部使用张量表示逻辑谓项（logic predicates）。基于这种张量表征，规则可以通过神经算子实现，且规则能应用于前提张量并生成归结张量。这样的神经算子是概率性的，并能通过各种命令（即使用不同元数在谓项上进行操作）处理关系型数据。

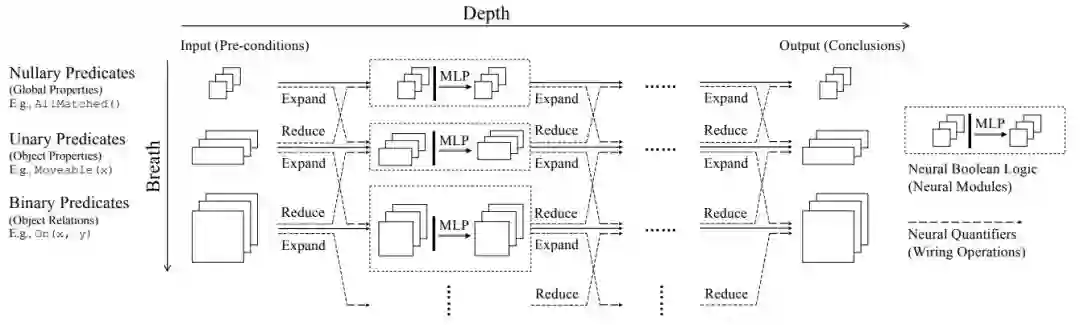
下图 2 展示了 NLM 整体的多层、多组架构。NLM 的层级深度为 D（水平向），每一层有 B+1 个计算单元（垂直向）。这些单元会在谓项的张量表征上进行操作，且谓项的元数（arity）在 [0, B] 之间。NLM 将谓项（前提）的张量作为输入，并执行一层层的计算，且把输出张量作为归结。

图 2：神经逻辑机（NLM）的整体架构。在前向传播中，NLM 将 object 属性和关系作为输入，并执行序列的逻辑演绎，最后输出归结属性或 object 间的关系。

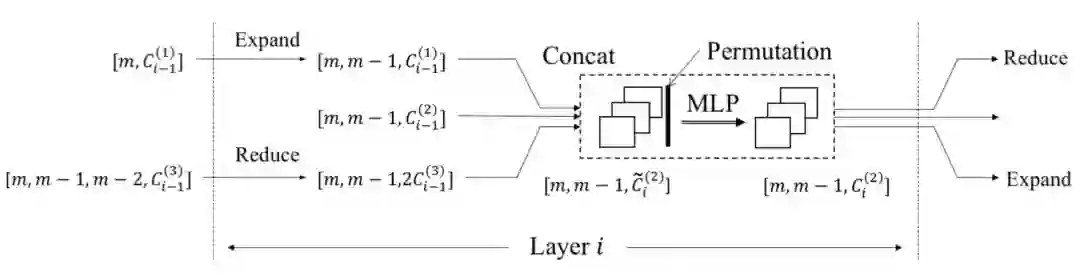
对于运算的具体内容，如下图 3 所示，如果层级 i 有的组为 2（二元谓项），那么模块从组内计算开始。它首先会收集垂直连续组（一元、二元和三元）的输出，该输出是从前一层 i-1 得到的，它们的张量形状见下图 3。

图 3：NLM 中的计算模块，以第 i 层的二元谓项为例。其中 C 的上下标分别表示组与层级，C 表示不同组与层级下的输出谓项数。[·] 表示张量形状。

实验

研究者在大量任务上对 NLM 进行了实验，包括关系推理、决策等。此外，研究者还证明使用小规模实例训练的 NLM 可以泛化到大规模实例上。在实验中，Softmax-Cross-Entropy 损失用于监督学习任务，REINFORCE (Williams, 1992) 用于强化学习任务。

研究者使用 Memory Networks (MemNN) (Sukhbaatar et al., 2015) 和 Differentiable Inductive Logic Programming (∂ILP) (Evans & Grefenstette, 2018) 分别作为联结主义和符号主义的基线模型。

家族树推理和图推理

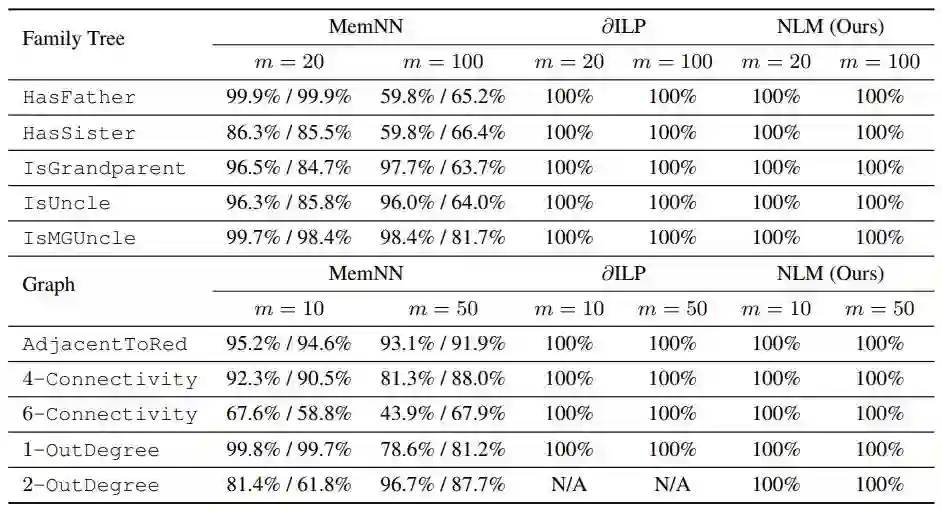
家族树是归纳逻辑程序设计的基准，在该任务中，向机器提供包含 m 个成员的家族树。该家族树由以下关系（谓项）表示：IsSon、IsDaughter、IsFather 和 IsMother。该任务的目标是推断出家族成员的其他属性或他们之间的关系。研究者还进一步将家族树扩展至通用图。

实验结果见表 1。

表 1：在家族树和图推理任务中，MemNN、∂ILP 和 NLM 的对比，其中 m 表示家族树或图的规模。∂ILP 和 NLM 的性能均优于神经基线模型，在测试集上达到了 100% 的准确率。注意：N/A 标记表示 ∂ILP 无法在 2-OutDegree 中扩展。

积木世界、排序和寻找最短路径

研究者在经典的积木世界问题（见图 1）上测试了 NLM 的决策性能，他们将 NLM 模型扩展至强化学习的马尔科夫决策过程（MDP）中。此外，研究者还在算法任务上测试了 NLM 的能力，如排序算法和路径算法。

NLM 在积木世界、排序和寻找最短路径任务上的性能如下所示：

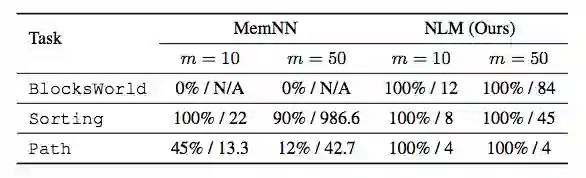
表 2：在积木世界、整数排序和寻找最短路径任务中，MemNN 和 NLM 的性能对比。

其中 m 表示积木世界环境中的积木数、排序环境中的数组规模，或者寻找最短路径环境中的图数量。两个模型都在 m ≤ 12 的情况下训练，在 m = 10 或 50 的情况下测试。性能评估指标有两个，由／分隔，二者分别是：测试中完成任务的概率、完成任务时智能体使用的平均步数。MemNN 无法在最大 m × 4 步数下完成积木世界任务。 

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者 / 实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告 & 商务合作：bd@jiqizhixin.com