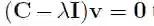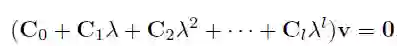【泡泡一分钟】稀疏消去法求解计算机视觉中的最优化问题 （ICCV2017-9）

每天一分钟，带你读遍机器人顶级会议文章

标题：Using Sparse Elimination for Solving Minimal Problems in Computer Vision

作者：Janne Heikkilä 

来源：International Conference on Computer Vision (ICCV 2017)

播音员：郭晨

编译：刘田

欢迎个人转发朋友圈；其他机构或自媒体如需转载，后台留言申请授权

摘要

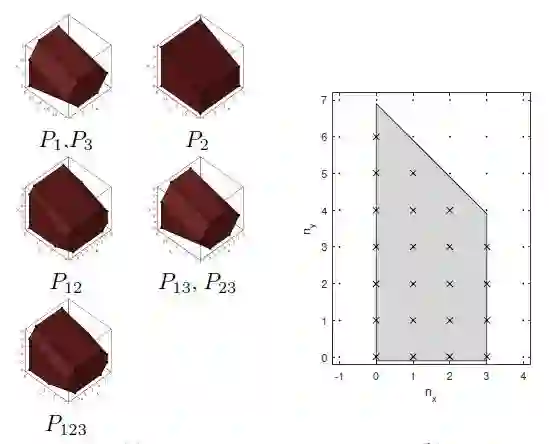
     今天向大家介绍的这篇文章理论含量100%，（车开了，请站稳扶好）多项式方程系统的闭式解是计算机视觉以及许多其他工程和科学领域经常要解决的问题。 Gröbner基方法给出了一种常用的提供解决方案，但是对于给定问题，实施高效的Gröbner基础求解器需要在代数几何中具有强大的专业知识。另一种方法是将方程转换为多项式特征值问题（PEP）并使用线性代数求解，对于不熟悉代数几何的人来说，这是一种易于理解的方法。因此，PEP已经成功地应用于求解计算机视觉中的一些相对姿态问题，但其更广泛的应用受限于找到紧凑单项基础的问题。

     本文提出了一种新的选择基的算法，该基通常比使用PEP作为求解多项式方程的最新算法获得的基更紧凑。本文的另一个贡献是提出了基于单应性的摄像机自我校准的两个最小问题，并且通过实验证明了我们的算法能够从两个未知平面场景的单应性矩阵为摄像机焦距提供数值稳定的解决方案。

------------------------------------------------------------------

注解：

PDE问题是求解特征值问题

的一种扩展：

Abstract

     Finding a closed form solution to a system of polynomial equations is a common problem in computer vision as well as in many other areas of engineering and science. Gröbner basis techniques are often employed to provide the solution, but implementing an efficient Gröbner basis solver to a given problem requires strong expertise in algebraic geometry. One can also convert the equations to a polynomial eigenvalue problem (PEP) and solve it using linear algebra, which is a more accessible approach for those who are not so familiar with algebraic geometry. In previous works PEP has been successfully applied for solving some relative pose problems in computer vision, but its wider exploitation is limited by the problem of finding a compact monomial basis. In this paper, we propose a new algorithm for selecting the basis that is in general more compact than the basis obtained with a state-of-the-art algorithm making PEP a more viable option for solving polynomial equations. Another contribution is that we present two minimal problems for camera self-calibration based on homography,and demonstrate experimentally using synthetic and real data that our algorithm can provide a numerically stable solution to the camera focal length from two homographies of unknown planar scence

如果你对本文感兴趣，想要下载完整文章进行阅读，可以关注【泡泡机器人SLAM】公众号（paopaorobot_slam）。

链接：https://pan.baidu.com/s/1mj3B34k 密码：qruw

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/forums/

泡泡机器人SLAM的原创内容均由泡泡机器人的成员花费大量心血制作而成，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！

商业合作及转载请联系liufuqiang_robot@hotmail.com