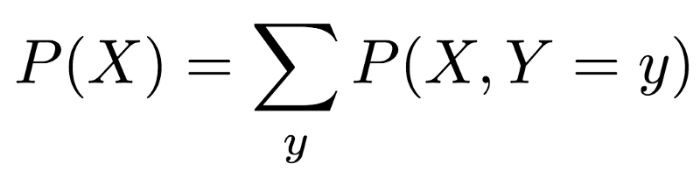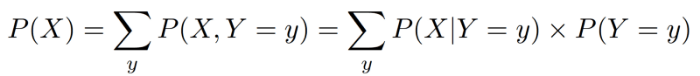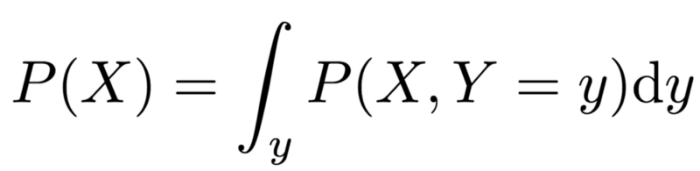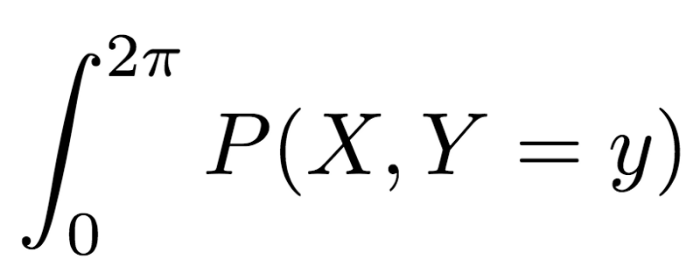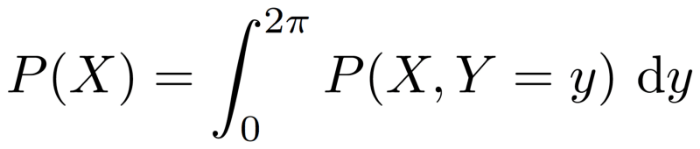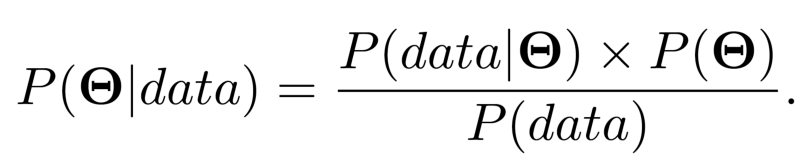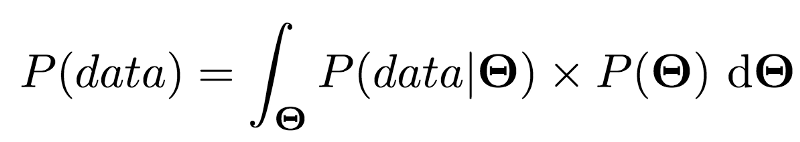零基础概率论入门：边缘化

作者：Jonny Brooks-Bartlett

编译：weakish

编者按：本文是数据科学家Jonny Brooks-Bartlett撰写的零基础概率论教程的第四篇，介绍了边缘化方法。

介绍

本文将通过解决一个相当简单的最大似然问题，介绍边缘化（marginalisation）的概念。本文涉及的一些基本概率概念可以参考本系列的第一篇文章。

什么是边缘化

边缘化是一种通过累加一个变量的可能值以判定另一个变量的边缘分布的方法。这听起来有点抽象，让我们看一个例子。

假设我们想知道天气是如何影响英国人的幸福感的，也就是P(幸福感|天气)。

假定我们具有衡量某人的幸福感所需的定义和设备，同时记录了某个英格兰人和某个苏格兰人所处位置的天气。可能苏格兰人通常而言要比英格兰人幸福。所以我们其实在衡量的是P(幸福感, 国|天气)，即，我们同时考察幸福感和国。

边缘化告诉我们，我们可以通过累加国家的所有可能值（英国由3国组成：英格兰、苏格兰、威尔士），得到想要计算的数字，即P(幸福感|天气) = P(幸福感, 国=英格兰|天气) + P(幸福感, 国=苏格兰|天气) + P(幸福感, 国=威尔士|天气)。

这就是了！边缘化让我们累加一些概率以得到想要计算的概率。一旦我们计算出了答案（可能是单一值或一个分布），我们可以得到所需的性质（推断）。

相关定义

如果这一概念让你觉得很耳熟，但你以前没有听过边缘化这个词，那可能是因为你听过它的另一个名字。有时这一方法称为对干扰变量积分（integrating out the nuisance variable）。积分本质上是累加一个变量的另一种说法，你正累加的变量称为“干扰变量”。所以在我们上面提到的例子中，“国”是干扰变量。

如果你正使用概率图模型，那么边缘化是进行精确推断的一种方法（也就是说，你可以写下你关注的分布的精确数值，例如可以基于分布精确计算的均值）。在这种情形下，边缘化有时和变量消除是同义词。

例子：未知骰子

下面的例子取自世界上最好的数学家和计算晶体学家之一Airlie J. McCoy所写的Liking likelihood论文。如果你正在寻找一篇基于骰子介绍各种最大似然概念（例如，对数似然、中心极限定理等)的文章，那么我强烈推荐这篇论文。

假设我们有4枚骰子：4面骰、6面骰、8面骰、10面骰（如下图所示）。

从左至右依次为：4面骰、6面骰、10面骰、8面骰

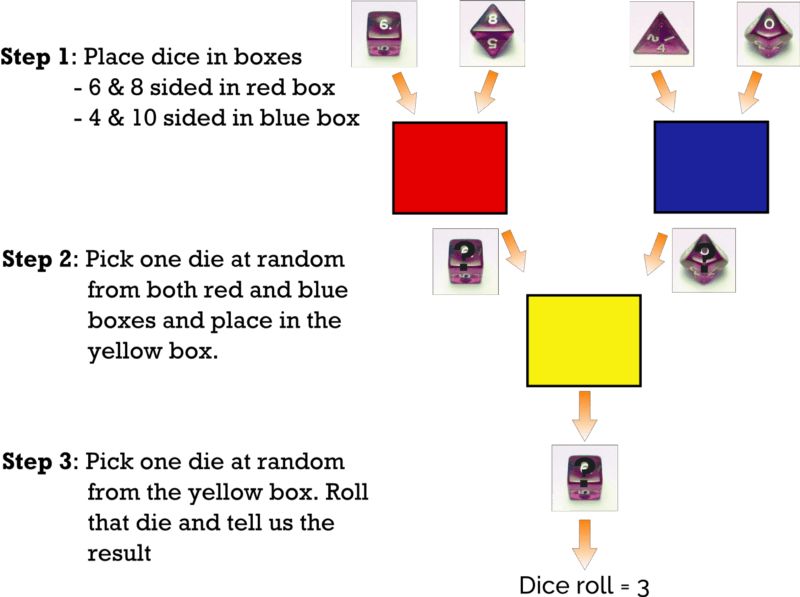
游戏

• 我把6面骰和8面骰放在红盒内，4面骰和10面骰放在蓝盒内。

• 我从红盒与蓝盒中分别随机选取一枚骰子，然后把它们放在黄盒内。

• 我从黄盒中随机选择一枚骰子，掷骰子并告诉你结果。

进行游戏之后，结果是3。我们想要回答的问题是：骰子更可能来自红盒还是蓝盒？

求解

为了求解这一问题，我们需要给定我们掷出了一个3这一条件后，骰子取自红盒的似然，L(盒=红|掷骰=3)，及相应的L(盒=蓝|掷骰=3)。这两个概率中较高的那个是问题的答案。

那么我们如何计算L(盒=红|掷骰=3)和L(盒=蓝|掷骰=3)呢？

首先，似然和概率的关系如下：

L(盒|掷骰) = P(掷骰|盒)

我的最大似然文章的结尾部分解释了这一等式。

这意味着，L(盒=红|掷骰=3)这一似然等价于给定骰子来自红盒这一条件，投掷出3点的概率，即P(掷骰=3|盒=红)。同理，L(盒=蓝|掷骰=3) = P(掷骰=3|盒=蓝)。

假定我们选择了一个红盒中的骰子。它可能是6面骰或8面骰（各自有50/50的机会）。假设我选择了6面骰。这意味着我必须从黄色盒子中选中6面骰，然后掷出3。这一情形的概率为：

P(掷骰=3, 骰=6面|盒=红) = 1/2 x 1/6

1/2是因为我有50%的机会从红盒中随机选中6面骰，因为盒中还有一枚8面骰。1/6是因为我有一枚6面骰，因此掷出3点的机会是1/6.

注意上面的答案没有包含从黄盒中选中6面骰的概率。这是因为，在这一情形下，从黄盒中选取6面骰的概率是1（你可能以为它是1/2，因为黄盒内有6面骰和从蓝盒中取出来的骰子）。这是因为我们正在计算的是给定骰子取自红盒的前提下一枚6面骰掷出一个3的条件概率。因此，我们选中黄盒中的另一枚骰子的情形是不可能存在的，因为那一枚骰子原本来自蓝盒。所以给定从红盒中取出骰子这一前提，我们只能从黄盒中选择6面骰，因而我们从黄盒中选中6面骰的概率是1。

类似地，我们可以计算结果为3，而我们实际上从红盒中选择了8面骰的概率：

P(掷骰=3, 骰=8面|盒=红) = 1/2 x 1/8

现在我们已经基本上完成了计算骰子来自红盒所需的计算工作。还记得吗？红盒只包含6面骰盒8面骰，因此我们只需找出骰子是6面或8面的概率。本系列的第一篇文章已经提过，这一“或”情形下，我们需要将概率相加。因此，骰子来自于红盒的概率为：

P(掷骰=3|盒=红) = (1/2 x 1/6) + (1/2 x 1/8) = 7/48

同理，骰子来自于蓝盒的概率为：

P(掷骰=3|盒=蓝) = P(掷骰=3, 骰=4面|盒=蓝) + P(掷骰=3, 骰=10面|盒=蓝) = (1/2 x 1/4) + (1/2 x 1/10) = 7/40

P(掷骰=3|盒=蓝)高于P(掷骰=3|盒=红)，基于最大似然，我们可以得出结论骰子更可能来自蓝盒。

这个例子中的边缘化在哪里？

非常善于观察的人会注意到，在上面的例子中，我没有用过“边缘化”这个词。这是因为我想让你直观地理解如何计算从盒子中取出骰子的概率。

如果你看一下上面计算蓝盒概率的等式，你会注意到我们把所有可能性（选择4面骰和10面骰）的概率加在一起。这正是边缘化！我们累加了这个干扰变量（骰子）。注意，游戏中我们从来没有观察到我们选择的骰子，而且我们不需要观察它！我们只需知道结果（掷骰=3）和骰子的所有可能值。这就是为什么边缘化如此强大。我们可以计算我们未曾观察到的事物的概率。只要我们知道可能的干扰变量值，我们就可以使用它进行边缘化操作，并计算另一个变量的分布。

记号

下面我会写下一些更吓人的公式，不过我会尽量让它们易于理解的。

回顾一下之前的例子。我们从一个联合概率开始，P(掷骰, 骰|盒)。边缘化之后，我们得到了一个条件概率，P(掷骰|盒)。这是边缘化的主要作用之一。我们可以从联合概率得到条件概率。

事实上我们也可以从联合概率得到边缘概率。如果你见过边缘化的数学定义，那么你多半看到的是一个边缘概率。如果你还没有见过边缘化的数学定义，那么，……你运气不错。你马上就可以见到了。

上式中大大的∑是累加的数学记号，下面的“y”告诉我们该累加什么。所以这个等式是说：“如果你想要得到X的边缘概率（等式左边），那么你需要对Y的每个可能值累加X和Y的联合概率。”

联合概率有时很难计算，所以我们可以使用本系列的第一篇文章中介绍的乘法法则将等式右边重写为以下形式：

等式的最右侧是条件分布和边缘分布的乘积，有时候这更容易计算。

正如我之前提到的的那样，∑让我们将所有项累加起来。我没有提到的是，这个符号只用于“离散”变量。在之前的例子中，我们累加的是离散的干扰变量（例如，UK只包括英格兰、苏格兰、威尔士，骰子的结果是有限的，比如1到6点）。不过，离散值不一定是有穷的。比如，所有正整数1、2、3、……也是离散值。

然而，当我们处理在给定的界限内有无穷的可能值的变量（例如，0到10米之间的距离可能有无穷的值，比如5米、5.1米、5.01米、5.001米、5.0001米……等等）时，我们将这些称为“连续变量”，同时我们不使用∑符号。相反，我们使用∫。这个符号仍然让我们把所有项累加起来，不过我们知道干扰变量是连续的，相应地，边缘化的定义为：

这和前面提到的离散变量的边缘化等式意义相同。等式末尾的“dy”告诉我们积分的项（“积分”是我们处理连续变量时所用的“累加”方法的名称）。

“dy”是必要的原因是如果我们不加以声明的话，积分的项并不总是显然的。考虑干扰变量是圆心角的情形。我们知道这个角位于0到360度之间，或者更技术性地说，我们更可能处理弧度而不是角度，这时我们说这个角位于0到2π之间。

（弧度，图片来源：维基百科）

所以我们可能尝试写下：

我们知道我们需要计算一个从0直到2π的积分，但我们知道积分的项是X的值还是Y的值吗？世界各地的数学家正迫不及待地要给我的脸上来一拳，以惩罚我上面的恶行。

为了修正这个问题，我们在结尾加上了“dy”，这样就很清楚了，我们积分的项是0到2π之间的Y的值，这意味着我们同时知道结果是X的边缘分布（见下）。

致感兴趣的读者，由于相位问题的存在，积分0至2π的角度是X射线晶体学（我的PhD领域）中需要进行的操作。基本上而言，相位问题指我们无法在实验中测量“相位”，而相位在数学上可以被看作一个角度。因此，为了计算观测数据的理论分布，我们需要边缘化相位。

adam kelleher在他的causality包中使用了边缘化以消除混淆变量（confounding variables）的影响。他同时像我们之前提到的一样使用乘法法则以条件分布和边缘分布乘积的形式书写了边缘化的定义。详见他写的博客。

结语

概率的链式法则

事实上，在上面的计算中我们应用了一个习以为常的概率过程，也就是概率的链式法则（不要和求导的链式法则混淆了）。概率的链式法则为：

P(A, B|C) = P(A|B, C) x P(B|C)

它让我们将一个联合概率（等式左侧）写成条件概率和边缘概率的乘积（等式右侧）。

计算联合概率时大量使用这一链式法则，正如我们之前提到的那样，判定条件概率和边缘概率可能要容易得多。

还记得我们在上面的计算中使用了下式吗？

P(掷骰=3, 骰=6面|盒=红) = 1/2 x 1/6

对比链式法则，我们令A = 掷骰，B = 骰，C = 盒。所以这意味着我们可以将上式左侧写为：

P(掷骰=3|骰=6面, 盒=红) x P(骰=6面|盒=红)

解释一下：

• P(掷骰=3|骰=6面, 盒=红)是给定我们选中了一枚6面骰，且这枚骰子曾经在红盒中这一前提，我们掷出3的概率。结果为1/6.

• P(骰=6面|盒=红)是给定我们从红盒中取出一枚骰子，这枚骰子是6面骰的概率。结果为1/2.

因此我们得到1/2 x 1/6，这正是我们在上面的例子中从直觉上得出的结果。

这里我们使用3个变量展示了链式法则。如果你看下维基百科上的链式法则的定义（看起来更可怕），你可以看到四个变量以及无穷变量的链式法则是什么样的。

维基百科上的链式法则定义看起来挺吓人的，但基本的想法是一样的。等式左侧是一个联合概率分布，等式右边是条件概率和边缘概率的乘积。

用于贝叶斯推断

如果你读过我之前关于贝叶斯推断的文章，你会知道贝叶斯理论的模型形式为：

正如我之前提过的那样，我们经常不计算分母P(data)，也就是归一化常量，因为在许多情形下它难以计算，而且我们并不总是需要计算它。

不过在某些情形下，我们可以借助边缘化精确地计算P(data)：

在某些情形下，我们可以演算这一式子（精确计算或在数值上逼近），因此我们可以得到一个归一化的后验分布。

谢谢你读到这里。我知道本文包含了很多数学，但我希望它是有意义的。如果文中有什么不清楚的地方，或者你希望我介绍什么内容，或者有什么地方可以改进的，别犹豫，留言告诉我。

谢谢！

原文地址：https://towardsdatascience.com/probability-concepts-explained-marginalisation-2296846344fc