Attention！神经网络中的注意机制到底是什么？

| 全文共3384字，建议阅读时长5分钟 |

原作：Adam Kosiorek
安妮 编译自 GitHub
转载公众号：量子位

微信号：QbitAI

神经网络的注意机制（Attention Mechanisms）已经引起了广泛关注。在这篇文章中，我将尝试找到不同机制的共同点和用例，讲解两种soft visual attention的原理和实现。

什么是attention？

通俗地说，神经网络注意机制是具备能专注于其输入（或特征）的神经网络，它能选择特定的输入。我们将输入设为x∈Rd，特征向量为z∈Rk，a∈[0,1]k为注意向量，fφ（x）为注意网络。一般来说，attention的实现方式为:

a=fφ（x）

或za=a⊙z

在上面的等式[1]中，⊙代表对应按元素（element-wise）相乘的运算。在这里我们引入soft attention和hard attention的概念，前者是指相乘时（soft）mask of values在0到1，而后者表示mask of values被强制分为0或1两种，也就是a∈{0,1}k。对于后者来说，我们能用hard attention掩饰指数特征向量：za=z[a]。这就增加了它的维度。

为了理解attention的重要性，我们需要考虑神经网络的本质——它是一个函数逼近器。依赖它的架构，它可以近似不同类型函数。神经网络一般被应用在链矩阵乘法和对应元素的架构中，在这些地方输入或特征向量仅在加法时相互作用。

注意机制可以用来计算可被用于特征相乘的mask，这种操作让神经网络逼近的函数空间大大扩展，使全新的用例成为可能。

Visual Attention

注意力可被应用在各种类型的输入，而无需考虑它们的形状。在像图像这种矩阵值输入的情况下，我们引入了视觉注意力这个概念。定义图像为I∈RH*W，g∈Rh*w为glimpse，也就是将注意机制应用于图像。

Hard Attention

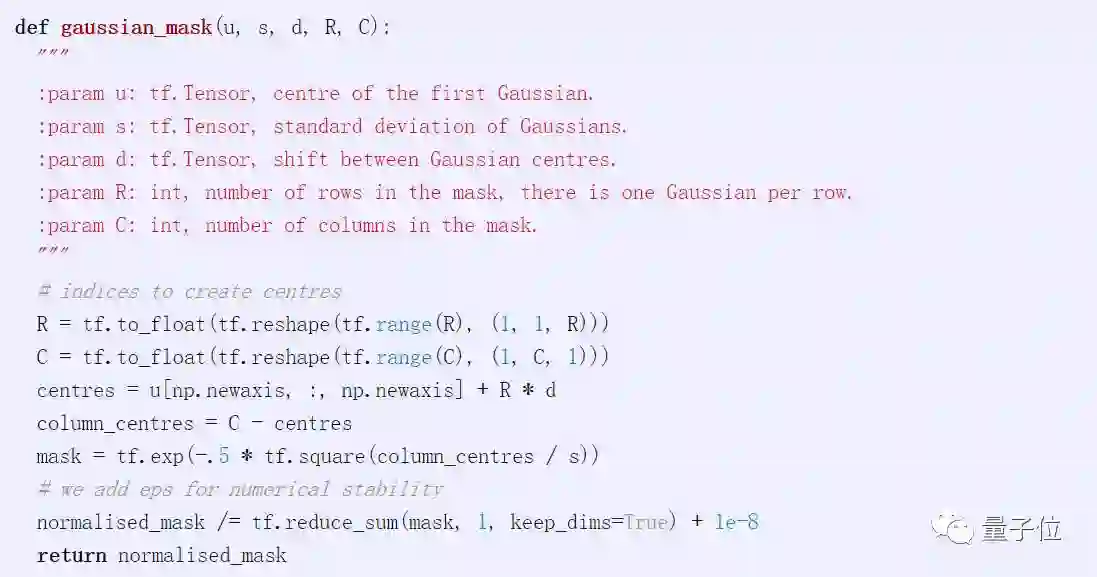
图像中的Hard Attentention 已经被应用很长时间了，比如图像裁剪。它的概念很简单，只需要编入索引（indexing）。Hard attention可在Python和TensorFlow中实现为：

上面这个形式的唯一问题是它是不可微分的，如果想了解模型的参数，则必须使用score-function estimator之类的帮助。

Soft Attention

在Attention最简单的变体中，soft attention对图像来说和公式[1]中实现的向量值特征没什么不同。论文《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》记录了它的早期应用。

论文地址：

https://arxiv.org/abs/1502.03044

这个模型学习图像特定的部分，同时生成描述该部分的语言。

然而，soft atttention用于计算有些不经济。输入中被遮蔽的部分对结果没有影响，但仍然需要进行运算。同时它也过参数化了，实现attention的Sigmoid激活函数是对彼此独立的。它可以一次选择多个目标，但在实践中，我们通常想有选择性地关注场景中一个或几个元素。

下面，我将分别由DRAW和Spatial Transformer Networks切入，介绍两种机制解决上述问题。它们还可以调整输入的大小，从而进一步提高性能。

DRAW介绍论文地址：

https://arxiv.org/abs/1502.04623

Spatial Transformer Networks介绍论文地址：

https://arxiv.org/abs/1506.02025

Gaussian Attention

Gaussian attention是用参数化的一维高斯滤波器创建一张图像大小的注意力地图。定义ay=Rh，ax=Rw为注意力向量，attention mask可被写成：

在上图中，顶行表示ax，最右列表示ay，中间的矩形表示a。为了让结果可视化，向量中只包含了0和1。在实践中，它们可以被一维高斯函数向量实现。一般来说，高斯函数的数目等同于空间维度，每一个向量都被三个参数表示：第一个高斯μ的中心，连续分布高斯中心之间的距离，高斯分布的标准差σ。有了这些参数变量，注意力和glimps都变得可微了，学习的难度也降低了不少。

因为上面这个例子只能选择一部分图像，剩余图像都需要被清理掉，因此用attention也显得有些不划算。如果我们不直接用向量，进而选择将它们分别形成矩阵Ay∈Rh*H和Ax∈Rw*W，可能会好些。

现在，每个矩阵的每一行都有一个Gaussian，并且参数d指定了连续行中高斯分布中心的特定距离。glimpse可以被表示为：

我将这个机制用在最近一篇对象跟踪的RNN attention的论文中，这篇是关于HART（Hierarchical Attentive Recurrent Tracking）的。

论文地址：

https://arxiv.org/abs/1706.09262

这里有一个例子，左边是输入图像，右边是attention,显示了绿色的主图像上的方框。

下面这串代码可以让你在TensorFlow中为小批量样例创建上述矩阵值mask。如果你想创建Ay，你可以称它为Ay = gaussian_mask(u, s, d, h, H)，其中u,s,d分别表示μ，σ和d，在这个方式中以像素的方式指定。

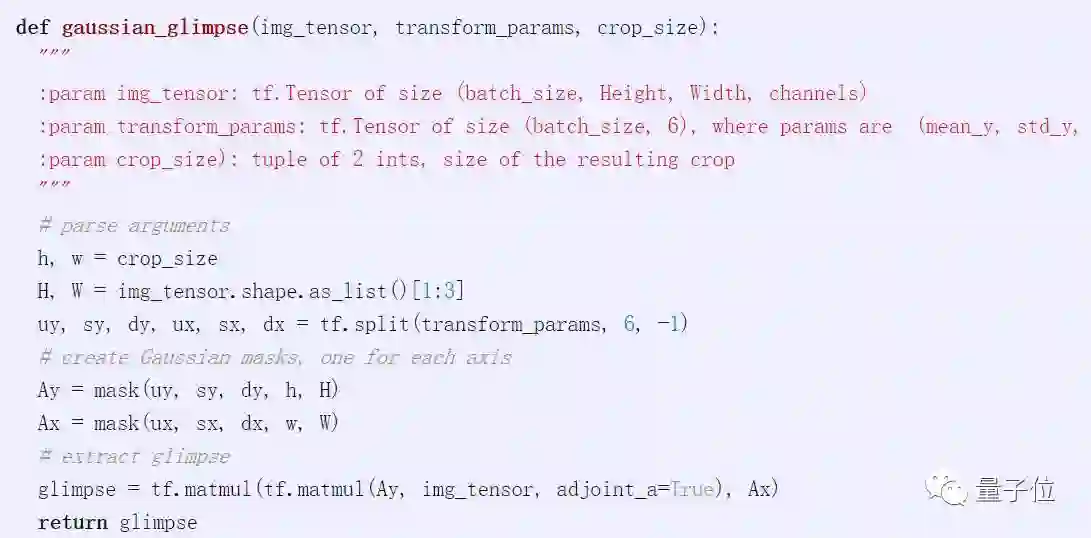
我们也可以编写一个函数来直接从图像中提取一个图像：

Spatial Transformer

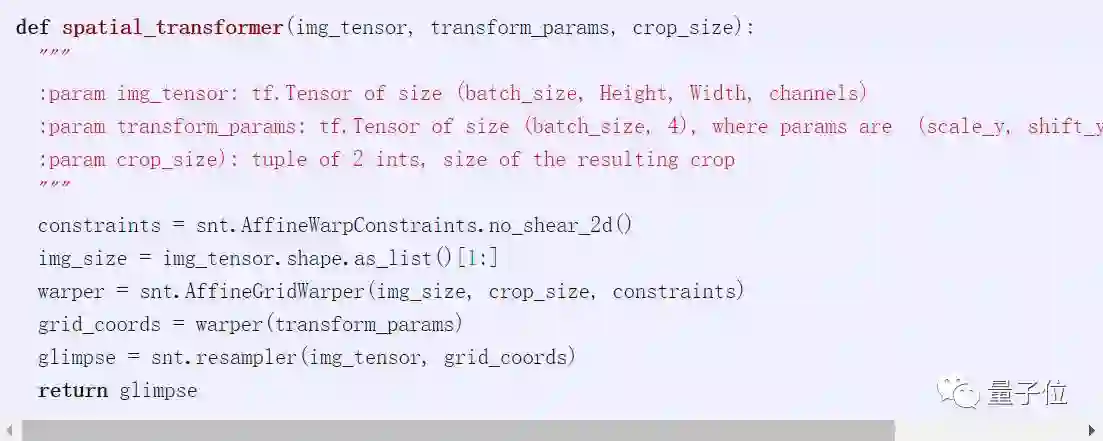
Spatial Transformer(STN)允许更一般转换，能区分图像裁剪。图像裁剪也是可能的用例之一，它由两个组件组成，网格生成器和采样器。网格生成器要指定从中取样的点网格，而采样器是样本。在DeepMind最近的神经网络库Sonnet中，用TensorFlow实现非常简单。

Gaunssian Attention vs. Spatial Transformer

Gaunssian Attention和Spatial Transformer实现的行为很相似，我们怎样判断选择哪一种实现方式呢？这里列举了一些细微差别：

Gaussian attention是一种超参数化的裁剪机制，它需要6个参数，但只有4个自由度(y,x，高度和宽度)。STN只需要四个参数。

目前我还没有运行任何测试，但是STN应该更快一些。它依赖于抽样点的线性插值，而Gaussian attention则需要执行两个矩阵乘法。

Gaussian attention应该更容易训练。这是因为，结果glimpse中每一个像素都可以是源图像相对较大像素块的凸组合，这使查找错因变得更加容易。另一方面，STN依赖于线性插值，在每个采样点处的梯度只在最接近的两个像素点处不为零。

结论

注意机制扩展了神经网络的功能，能近似更复杂的函数。或者用更直观的术语来说，它能够专注于输入的特定部分，提高了自然语言基准测试的性能，也带来了全新的功能，如图像字幕、内存网络中地址和神经程序。

我认为，attention最重要的应用案例尚未被发现。举个例子，我们知道视频中的对象是一致和连贯的，它们不会在帧与帧中突然消失。注意机制可以用来表示这种一致性。至于它的后续发展如何，我会持续关注。

有缘的人终会相聚，慕客君想了想，要是不分享出来，怕我们会擦肩而过~

《预约、体验——新维空间站》

《【会员招募】“新维空间站”1年100场活动等你来加入》

《有缘的人总会相聚——MOOC公号招募长期合作者》

《【调查问卷】“屏幕时代，视觉面积与学习效率的关系“——你看对了吗？》

本文编辑：慕编组成员（杨佳朋）

产权及免责声明

本文系“MOOC”公号转载、编辑的文章，编辑后增加的插图均来自于互联网，对文中观点保持中立，对所包含内容的准确性、可靠性或者完整性不提供任何明示或暗示的保证，不对文章观点负责，仅作分享之用，文章版权及插图属于原作者。如果分享内容侵犯您的版权或者非授权发布，请及时与我们联系，我们会及时内审核处理。

了解在线教育，
把握MOOC国际发展前沿，请关注：
微信公号：openonline
公号昵称：MOOC