GNN如何统一谱域与空间？CVPR2024教程《统一谱域和空间图神经网络》，87页ppt

6 月 17 日至 21 日，计算机视觉领域顶级盛会之一国际计算机视觉与模式识别会议（CVPR 2024）将在加拿大温哥华举行。CVPR（Computer Vision and Pattern Recognition，计算机视觉与模式识别）会议是计算机视觉与模式识别、人工智能领域的国际顶级会议，是中国计算机学会（CCF）推荐的A类国际学术会议。本届会议录用率为23.6%。

来自Mississippi State University给出了《谱域空间图神经网络》教程，值得关注！

近年来，图神经网络（Graph Neural Networks, GNNs）引起了广泛关注。然而，各种理论方法支撑下的多样化GNN模型的涌现，使得模型选择过程变得复杂，因为它们并不能在一个统一的框架内轻松理解。具体来说，早期的GNN是基于谱域理论实现的，而其他GNN则基于空间理论开发。这种谱域方法和空间方法之间的分歧使得直接比较变得具有挑战性。此外，每个领域内部的众多模型进一步加剧了对其各自优劣的评估复杂性。在这个半天的教程中，我们将探讨GNN的最新进展，并引入一个综合框架，连接空间和谱域领域，阐明它们的复杂相互关系。这种对综合框架的强调增强了我们对GNN操作的理解。教程的目的是通过谱域图论和逼近理论的综合来探讨关键范式（如基于空间和基于谱域的方法）之间的相互作用。我们在本教程中对GNN的最新研究进展进行了深入分析，包括讨论如过度平滑等新兴问题。将使用一系列成熟的GNN模型来说明我们提出的框架的普遍性。

分发的材料/资源

• CVPR 2024教程官方网站
• CVPR 24’教程版本的幻灯片
• 主要参考论文（发表在ACM Computing Survey上）
• GitHub上的相关资源集合

主讲人、时间和地点

• 地点：440-441会议室
• 时间：2024年6月18日下午2点

**主讲人

• Dr. Zhiqian Chen @ 密西西比州立大学
• Dr. Lei Zhang @ 弗吉尼亚理工大学
• Dr. Liang Zhao @ 埃默里大学

计划概述

教程总时长为150分钟，包含教程时间、15分钟休息时间和15分钟问答时间。

**1. 背景：谱域和空间图神经网络（20分钟）

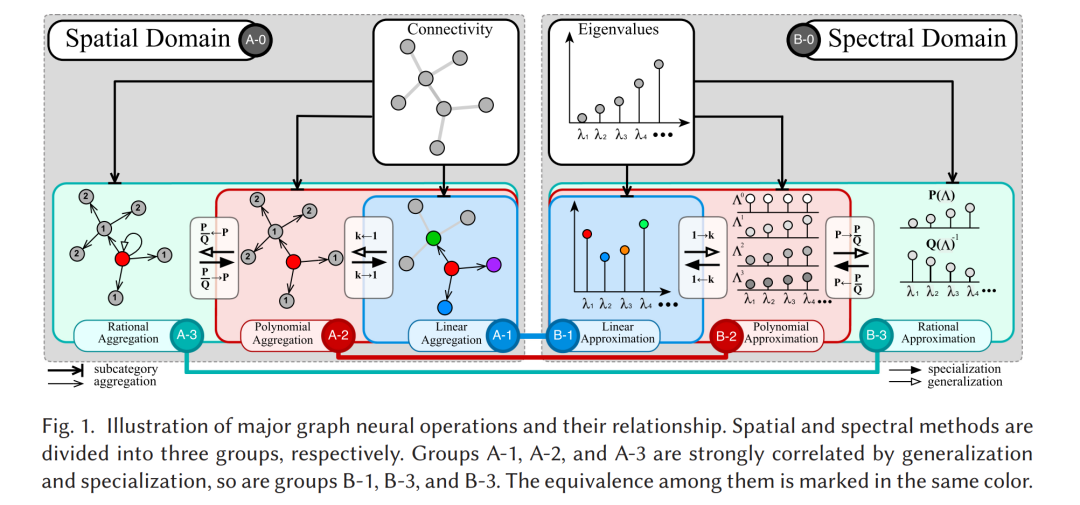
GNN可以根据其基础计算机制分为两大类：谱域方法和空间方法。谱域GNN基于图信号处理，依赖于图拉普拉斯算子的特征分解，具有如ChebNet等基础贡献。这些网络为图上的卷积操作提供了理论上强有力的框架，尽管在计算资源方面可能较为苛刻。相比之下，空间GNN在顶点域内操作，从邻居节点聚合信息，代表性模型有GraphSAGE和GCN。本教程将全面介绍谱域和空间GNN的最新进展，并从技术角度详细分析这两种GNN范式的演变。在每种类别的GNN中，都存在指导其设计的多种理论基础。这种多样性使得在不同的GNN框架之间进行统一分析变得具有挑战性。为克服这一障碍，我们将探讨一种我们提出的新视角，可能将两种类型在一个统一的框架内进行处理，并随后讨论其优缺点。

• 图神经网络当前研究（5分钟）
• 基于空间的GNN概述（5分钟）
• 基于谱域的GNN概述（5分钟）
• 研究空间和谱域GNN连接的挑战和益处（5分钟）

**2. 谱域图论、逼近理论和GNN（50分钟）

在本部分中，我们将通过案例研究和全面的理论解释阐明我们提出的统一视角。例如，作为基本操作之一，我们将从谱域和空间视角分别考察图矩阵归一化，充分证明归一化的必要性。此外，我们将深入探讨图卷积的谱域和空间视角：谱域图论致力于通过与图相关的矩阵（特别是邻接矩阵或拉普拉斯矩阵）的特征向量和特征值来分析图结构。逼近理论关注在指定函数类中寻找函数的最佳逼近，这在揭示特征值函数的表达能力方面起着关键作用。通过结合谱域和逼近方法，我们可以将所有GNN分类为线性、多项式和有理函数。相应地，空间方法可以分为邻居之间的一阶、高阶和跳跃连接策略。这两套三层分类精确对应，提供了额外的见解，使我们提出的视角既统一又有助于阐明更广泛的GNN。

• 谱域图论（15分钟）
• GNN的逼近理论：线性、多项式和有理函数（15分钟）
• 案例研究：归一化、GCN和DeepWalk（15分钟）
• 统一框架以桥接空间和谱域GNN（5分钟）

**3. 理论研究：不确定性、采样过度平滑和逆问题的视角（60分钟）

本节提供了对图神经网络（GNNs）领域内普遍话题（如不确定性、采样、过度平滑和逆问题）的深刻且创新的理论视角，旨在为分析和理解GNN中的各种现象提供综合框架。此外，这些新见解可以通过谱域和空间视角进行解释。不确定性原理用于理解在谱域和空间域中可观察到的不同全局和局部效应。图采样理论的检查通过一个统一框架来实现，该框架集成了显式的闭式解。GNN中的过度平滑现象，随着连续层的应用节点特征的独特性减少，可以在相同的概念框架内进行解释。逆问题领域，专注于解决图中的边相关问题，为理解GNN提供了另一种视角。

• 不确定性原理：全局与局部视角（10分钟）
• 空间和谱域方法的理论比较（10分钟）
• 采样视角（15分钟）
• 过度平滑视角（15分钟）
• 逆问题视角（10分钟）

**4. 未来方向（20分钟）

使用偏微分方程（PDEs）进行图分析的最新进展显示出前景。具体来说，这种情况下多项式和有理函数的行为与扩散和波函数相似，提供了利用这些函数研究GNN的创新工具。然而，目前的谱域图论主要适用于简单图。扩展这些理论以涵盖有符号、定向和超图仍然是一个未开发的领域。尽管已经取得了一些进展，但整合这些图类型的综合理论框架仍在开发中。未来的研究将探讨制定统一谱域理论的可行性。该理论不仅涵盖各种图类型，包括简单图、有符号图、定向图和超图，还将解决这些图固有的动态。目标是创建对各种图类型及其动态行为和特性的整体和集成的理论理解。

• 图上的偏微分方程（10分钟）
• 非简单图的谱域图论（5分钟）
• 图动态（5分钟）

**5. 结论与讨论（15分钟）

• 结论（5分钟）
• 问答（10分钟）

综述论文

深度学习的性能在最近得到了广泛认可。图神经网络（GNN）旨在处理经典深度学习难以管理的图结构数据。由于大多数GNN是使用不同的理论创建的，因此无法进行直接比较。先前的研究主要集中在对现有模型进行分类，而很少关注它们内在的联系。本研究的目的是建立一个基于谱图理论和近似理论的统一框架，将GNN整合在一起。该框架实现了空间和谱基于GNN之间的紧密集成，同时紧密关联了各自领域内存在的方法。

引言

深度学习在各种机器学习任务中的表现已经在过去几十年里得到了广泛认可，尤其在欧几里得数据上取得了惊人的成功。在过去几十年里，出现了一系列新的应用，这些应用中有效的信息分析归结为用图表示的数据的非欧几里得几何，例如社交网络、交通网络、流行病传播、脑神经网络、生物调控网络上的基因数据、电信网络和知识图谱。以前的深度学习算法（如卷积神经网络和循环神经网络）无法处理图结构数据上的这种非欧几里得问题。用图来建模数据是困难的，因为图数据是不规则的，即每个图都有不同数量的节点，每个节点在图中都有不同数量的邻居，使得一些操作（如卷积）在网络结构中不可用。

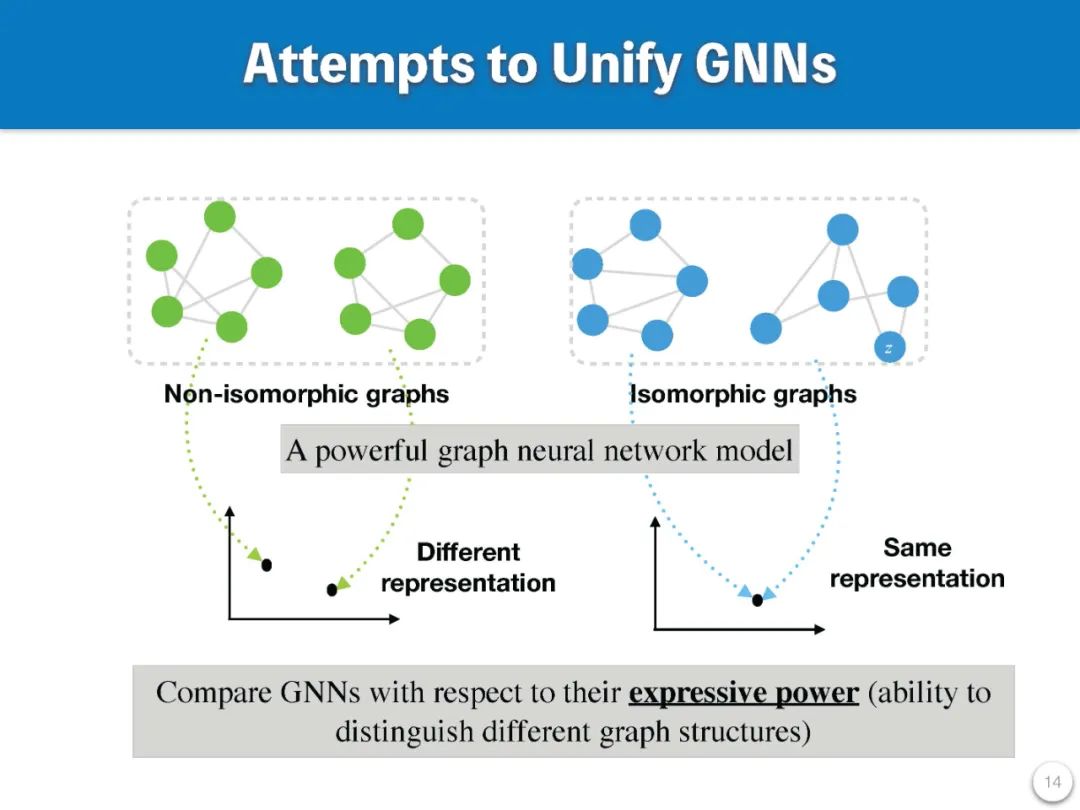
最近，应用深度学习于图数据的兴趣激增。受深度学习成功的启发，从深度学习模型中借鉴的原理被用来处理图的固有复杂性。这一增长趋势引起了机器学习社区的兴趣，提出了大量基于不同理论的图神经网络（GNN）模型【7–12】，并将其分为谱域【13–17】和空间域【10–12】两大类。GNN最近在学习图表示方面越来越受欢迎，并迅速扩展到许多应用领域，如物理学【18, 19】、化学【20, 21】、知识图谱【22–25】、推荐系统【26–29】、计算机视觉【30–32】、自然语言处理【33–35】、组合优化【36–38】、交通网络【39–42】、程序表示【43–45】、社交网络【26, 46, 47】。然而，当前的方法论研究并未转化为对所涉及机制的清晰理解，也未能为我们提供关于GNN有效性或物理意义的洞见。因此，将会出现以下几种结果：（1）没有将所有GNN连接起来的基本原理，这也限制了它们的发展。（2）在诸如药物开发等高风险应用中，GNN模型可能存在潜在的未知风险，因为它们是黑箱。因此，剖析GNN的必要性被突显出来，从而推动学者们寻找一个更普遍的框架。主要问题在于现有的GNN模型使用了多种技术，包括随机游走【48–50】、PageRank【51–54】、注意力模型【12, 55, 56】、低通滤波器【57, 58】和消息传递【59, 60】。一些初步研究只能解释少数GNN方法【59, 61, 62】，大多数GNN未被解释。以往的GNN综述大多处理将几种现有模型分类成多个类别，并分别扩展每个类别，而不考虑它们之间的相互关系【13–17】。

本研究旨在通过弥合空间和谱域中看似不相关的工作之间的鸿沟，以及通过连接每个域内的方法，提供一个统一的框架来推广GNN。该研究将构建一个涵盖多种GNN的统一理论框架。我们的研究的新颖之处在于它连接了不同的GNN模型，允许对所有GNN模型进行直接的重新思考和比较。