会员服务
math · 数值分析 · Maple · MATLAB · 密西西比大学 ·
2022 年 3 月 19 日
640页《利用Maple和Matlab进行数值分析》，密西西比大学Seongjai Kim教授最新讲义
专知会员服务
专知会员服务
专知，提供专业可信的知识分发服务，让认知协作更快更好！

【作者简介】
Seongjai Kim

  • 密西西比州立大学数学与统计系教授
  • 研究兴趣：
    • 数学、计算和工程
      • 机器学习
      • 数据分析：大数据和小数据
      • 实时系统开发
    • 教育与宇宙学
      • 数学和计算机教育
      • 宇宙学：前大爆炸理论

个人主页：
https://skim.math.msstate.edu/index.html

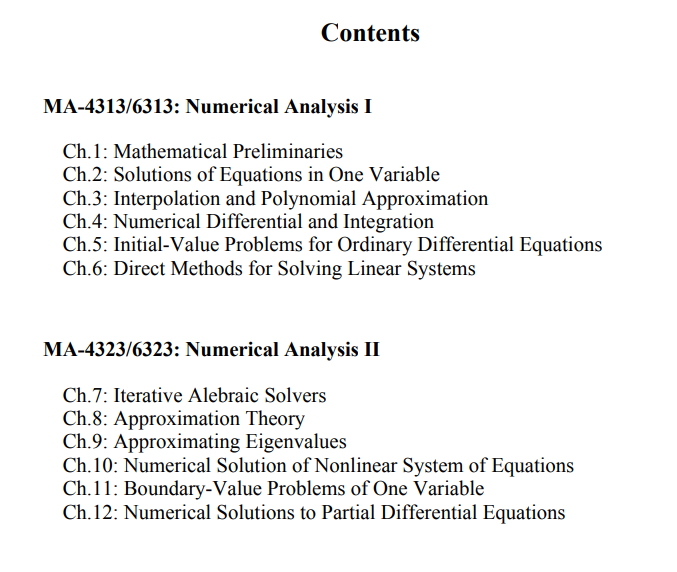
【讲稿】


成为VIP会员查看完整内容
1到6章 Numerical_Analysis_Lecture-Ch.01-06 7到12章 NA2_Lecture_Chap.07-12
27

相关内容

MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
专知会员服务
157+阅读 · 2022年4月17日
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义，Fundamentals of Numerical Linear Algebra
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义，Fundamentals of Numerical Linear Algebra
专知会员服务
43+阅读 · 2022年3月18日
407页《偏微分方程的数值解法》，密西西比大学Seongjai Kim教授最新讲义
407页《偏微分方程的数值解法》，密西西比大学Seongjai Kim教授最新讲义
专知会员服务
46+阅读 · 2022年3月17日
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授，Mathematical Foundations of Machine Learning
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授，Mathematical Foundations of Machine Learning
专知会员服务
123+阅读 · 2022年3月7日
帝国理工学院114页机器学习中的数学知识（附下载）
帝国理工学院114页机器学习中的数学知识（附下载）
专知会员服务
36+阅读 · 2022年2月27日
【经典书】凸优化理论，MIT-Dimitri P. Bertsekas教授，257页pdf
【经典书】凸优化理论，MIT-Dimitri P. Bertsekas教授，257页pdf
专知会员服务
75+阅读 · 2021年8月28日
机器学习简明导论，62页pdf
专知会员服务
80+阅读 · 2021年7月31日
【干货书】计算机科学家的数学，153页pdf
【干货书】计算机科学家的数学，153页pdf
专知会员服务
170+阅读 · 2021年7月27日
商业数据分析，39页ppt
商业数据分析，39页ppt
专知会员服务
160+阅读 · 2020年6月2日
【2020新书】利用Simulink进行MATLAB仿真，对常微分方程和偏微分方程进行编程和仿真，495pdf
【2020新书】利用Simulink进行MATLAB仿真，对常微分方程和偏微分方程进行编程和仿真，495pdf
专知会员服务
68+阅读 · 2020年4月10日
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
专知
3+阅读 · 2022年4月17日
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义
专知
0+阅读 · 2022年3月19日
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授
专知
2+阅读 · 2022年3月16日
美国工程院院士MIT教授Dimitri2022新书《AlphaZero最优模型预测与自适应控制》，(附书稿PDF&讲义)
美国工程院院士MIT教授Dimitri2022新书《AlphaZero最优模型预测与自适应控制》，(附书稿PDF&讲义)
专知
1+阅读 · 2022年1月3日
【经典书】应用离散结构，568页pdf
【经典书】应用离散结构，568页pdf
专知
2+阅读 · 2021年5月4日
直白生动！《机器学习知识点彩图版》297页ppt以图画式描述机器学习中的知识点
直白生动！《机器学习知识点彩图版》297页ppt以图画式描述机器学习中的知识点
专知
2+阅读 · 2021年3月11日
【加州理工】什么是模仿学习(Imitation Learning（模仿学习), 这62页ppt带你了解进展，附下载
【加州理工】什么是模仿学习(Imitation Learning（模仿学习), 这62页ppt带你了解进展，附下载
专知
20+阅读 · 2019年11月14日
普林斯顿大学19年春季学期《机器学习优化》课程讲义
普林斯顿大学19年春季学期《机器学习优化》课程讲义
专知
12+阅读 · 2019年6月13日
246 页《统计机器学习与凸优化》教程 PPT 下载
246 页《统计机器学习与凸优化》教程 PPT 下载
新智元
24+阅读 · 2018年9月21日
机器学习数学基础【附PPT下载】
机器学习数学基础【附PPT下载】
专知
45+阅读 · 2018年9月17日
四阶微分方程的谱和谱元方法
国家自然科学基金
0+阅读 · 2014年12月31日
高能量粒子驱动的环形阿尔芬本征模数值模拟研究
国家自然科学基金
0+阅读 · 2014年12月31日
南京民国建筑修缮BIM模型实例库的构建及其数据挖掘与知识发现研究
国家自然科学基金
1+阅读 · 2014年12月31日
非均匀介质内传输问题及其特征值问题的数值方法研究
国家自然科学基金
0+阅读 · 2013年12月31日
基于微分方程模型的介质成像和图像处理的数值方法
国家自然科学基金
0+阅读 · 2013年12月31日
离散HJB方程及离散HJB障碍问题的快速迭代算法研究
国家自然科学基金
0+阅读 · 2012年12月31日
新一代产品几何量技术规范的范畴纤维化模型及智能专家系统的研究与开发
国家自然科学基金
1+阅读 · 2012年12月31日
约束非线性全局优化的辅助函数方法研究
国家自然科学基金
0+阅读 · 2009年12月31日
基于神经网络模型脉冲同步的保密通信方案的研究
国家自然科学基金
0+阅读 · 2009年12月31日
大气、海洋科学中偏微分方程和随机动力系统的研究
国家自然科学基金
0+阅读 · 2008年12月31日
Sheaf semantics of termination-insensitive noninterference
Arxiv
0+阅读 · 2022年4月20日
Who Is Missing? Characterizing the Participation of Different Demographic Groups in a Korean Nationwide Daily Conversation Corpus
Arxiv
1+阅读 · 2022年4月20日
Simulating Interaction Movements via Model Predictive Control
Arxiv
0+阅读 · 2022年4月19日
Formalizing Geometric Algebra in Lean
Arxiv
0+阅读 · 2022年4月19日
Dual-Domain Image Synthesis using Segmentation-Guided GAN
Arxiv
0+阅读 · 2022年4月19日
Quantum Bayesian Statistical Inference
Arxiv
0+阅读 · 2022年4月19日
Optimal bounds for numerical approximations of infinite horizon problems based on dynamic programming approach
Arxiv
1+阅读 · 2022年4月19日
Accurate 3D Hand Pose Estimation for Whole-Body 3D Human Mesh Estimation
Arxiv
0+阅读 · 2022年4月19日
Turing's cascade instability supports the coordination of the mind, brain, and behavior
Arxiv
0+阅读 · 2022年4月17日
Exponential Integration for Efficient and Accurate Multi-Body Simulation with Stiff Viscoelastic Contacts
Arxiv
0+阅读 · 2022年4月16日
VIP会员
相关主题
math
数值分析
Maple
MATLAB
密西西比大学
相关VIP内容
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
专知会员服务
157+阅读 · 2022年4月17日
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义，Fundamentals of Numerical Linear Algebra
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义，Fundamentals of Numerical Linear Algebra
专知会员服务
43+阅读 · 2022年3月18日
407页《偏微分方程的数值解法》，密西西比大学Seongjai Kim教授最新讲义
407页《偏微分方程的数值解法》，密西西比大学Seongjai Kim教授最新讲义
专知会员服务
46+阅读 · 2022年3月17日
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授，Mathematical Foundations of Machine Learning
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授，Mathematical Foundations of Machine Learning
专知会员服务
123+阅读 · 2022年3月7日
帝国理工学院114页机器学习中的数学知识（附下载）
帝国理工学院114页机器学习中的数学知识（附下载）
专知会员服务
36+阅读 · 2022年2月27日
【经典书】凸优化理论，MIT-Dimitri P. Bertsekas教授，257页pdf
【经典书】凸优化理论，MIT-Dimitri P. Bertsekas教授，257页pdf
专知会员服务
75+阅读 · 2021年8月28日
机器学习简明导论，62页pdf
专知会员服务
80+阅读 · 2021年7月31日
【干货书】计算机科学家的数学，153页pdf
【干货书】计算机科学家的数学，153页pdf
专知会员服务
170+阅读 · 2021年7月27日
商业数据分析，39页ppt
商业数据分析，39页ppt
专知会员服务
160+阅读 · 2020年6月2日
【2020新书】利用Simulink进行MATLAB仿真，对常微分方程和偏微分方程进行编程和仿真，495pdf
【2020新书】利用Simulink进行MATLAB仿真，对常微分方程和偏微分方程进行编程和仿真，495pdf
专知会员服务
68+阅读 · 2020年4月10日
热门VIP内容
相关资讯
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
MIT科学家Dimitri P. Bertsekas最新《强化学习与最优控制》2022ASU课程，(附书稿PDF&讲义)
专知
3+阅读 · 2022年4月17日
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义
265页《数值线性代数基础》，密西西比大学Seongjai Kim教授最新讲义
专知
0+阅读 · 2022年3月19日
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授
【2022新书】机器学习数学基础，328页pdf，密西西比州立大学Seongjai Kim教授
专知
2+阅读 · 2022年3月16日
美国工程院院士MIT教授Dimitri2022新书《AlphaZero最优模型预测与自适应控制》，(附书稿PDF&讲义)
美国工程院院士MIT教授Dimitri2022新书《AlphaZero最优模型预测与自适应控制》，(附书稿PDF&讲义)
专知
1+阅读 · 2022年1月3日
【经典书】应用离散结构，568页pdf
【经典书】应用离散结构，568页pdf
专知
2+阅读 · 2021年5月4日
直白生动！《机器学习知识点彩图版》297页ppt以图画式描述机器学习中的知识点
直白生动！《机器学习知识点彩图版》297页ppt以图画式描述机器学习中的知识点
专知
2+阅读 · 2021年3月11日
【加州理工】什么是模仿学习(Imitation Learning（模仿学习), 这62页ppt带你了解进展，附下载
【加州理工】什么是模仿学习(Imitation Learning（模仿学习), 这62页ppt带你了解进展，附下载
专知
20+阅读 · 2019年11月14日
普林斯顿大学19年春季学期《机器学习优化》课程讲义
普林斯顿大学19年春季学期《机器学习优化》课程讲义
专知
12+阅读 · 2019年6月13日
246 页《统计机器学习与凸优化》教程 PPT 下载
246 页《统计机器学习与凸优化》教程 PPT 下载
新智元
24+阅读 · 2018年9月21日
机器学习数学基础【附PPT下载】
机器学习数学基础【附PPT下载】
专知
45+阅读 · 2018年9月17日
相关基金
四阶微分方程的谱和谱元方法
国家自然科学基金
0+阅读 · 2014年12月31日
高能量粒子驱动的环形阿尔芬本征模数值模拟研究
国家自然科学基金
0+阅读 · 2014年12月31日
南京民国建筑修缮BIM模型实例库的构建及其数据挖掘与知识发现研究
国家自然科学基金
1+阅读 · 2014年12月31日
非均匀介质内传输问题及其特征值问题的数值方法研究
国家自然科学基金
0+阅读 · 2013年12月31日
基于微分方程模型的介质成像和图像处理的数值方法
国家自然科学基金
0+阅读 · 2013年12月31日
离散HJB方程及离散HJB障碍问题的快速迭代算法研究
国家自然科学基金
0+阅读 · 2012年12月31日
新一代产品几何量技术规范的范畴纤维化模型及智能专家系统的研究与开发
国家自然科学基金
1+阅读 · 2012年12月31日
约束非线性全局优化的辅助函数方法研究
国家自然科学基金
0+阅读 · 2009年12月31日
基于神经网络模型脉冲同步的保密通信方案的研究
国家自然科学基金
0+阅读 · 2009年12月31日
大气、海洋科学中偏微分方程和随机动力系统的研究
国家自然科学基金
0+阅读 · 2008年12月31日
相关论文
Sheaf semantics of termination-insensitive noninterference
Arxiv
0+阅读 · 2022年4月20日
Who Is Missing? Characterizing the Participation of Different Demographic Groups in a Korean Nationwide Daily Conversation Corpus
Arxiv
1+阅读 · 2022年4月20日
Simulating Interaction Movements via Model Predictive Control
Arxiv
0+阅读 · 2022年4月19日
Formalizing Geometric Algebra in Lean
Arxiv
0+阅读 · 2022年4月19日
Dual-Domain Image Synthesis using Segmentation-Guided GAN
Arxiv
0+阅读 · 2022年4月19日
Quantum Bayesian Statistical Inference
Arxiv
0+阅读 · 2022年4月19日
Optimal bounds for numerical approximations of infinite horizon problems based on dynamic programming approach
Arxiv
1+阅读 · 2022年4月19日
Accurate 3D Hand Pose Estimation for Whole-Body 3D Human Mesh Estimation
Arxiv
0+阅读 · 2022年4月19日
Turing's cascade instability supports the coordination of the mind, brain, and behavior
Arxiv
0+阅读 · 2022年4月17日
Exponential Integration for Efficient and Accurate Multi-Body Simulation with Stiff Viscoelastic Contacts
Arxiv
0+阅读 · 2022年4月16日
微信扫码咨询专知VIP会员
Top