哥伦比亚大学最新博士论文《机器学习在金融市场中的应用》Essays on the Applications of Machine Learning in Financial Markets

摘要

我们考虑资产管理中常见的问题，例如最优执行、投资组合构建和交易策略实施。这些问题在实践中通常是困难的，很大程度上是由于金融市场的不确定性。在本论文中，我们通过机器学习开发数据驱动的方法，以更好地解决这些问题并改善金融市场的决策。机器学习是指捕获数据模式的一类统计方法。几十年来，回归等传统方法已广泛应用于金融领域。在某些情况下，这些方法已成为实证金融研究中许多基本理论的重要组成部分。然而，诸如基于树的模型和神经网络等较新的方法在金融文献中仍然难以捉摸，并且它们在金融领域的可用性仍然知之甚少。本论文的目的是了解这些新的机器学习方法带来的各种权衡，以及它们可以在多大程度上提高市场参与者的效用。

在本文的第一部分，我们考虑了使用市场订单和限价订单之间的决策。这是实际最优交易中的一个重要问题。做出此决定的关键因素是了解限价订单执行的不确定性，即成交概率或订单将在特定时间范围内执行的概率。同样，我们可以估计填充时间的分布。我们提出了一种基于循环神经网络的数据驱动方法，以根据当前市场条件估计限价订单的成交时间分布。通过使用历史数据集，我们展示了这种方法相对于几种基准测试技术的优越性。当在一个典型的交易问题中执行交易策略时，这种方法也会导致显著的成本降低。

在论文的第二部分，我们将一个高频最优执行问题表述为一个最优停止问题。通过强化学习，我们开发了一种数据驱动的方法，将价格可预测性和限制订单量的动态结合起来。用深度神经网络来表示延续值。我们的方法优于基准方法，包括基于价格预测的监督学习方法。通过历史上的NASDAQ ITCH数据集，我们证明了成本的显著降低。在时间差分学习和蒙特卡罗方法之间的各种折衷也被讨论。另一个有趣的观点是，股票之间存在一定的普遍性——从一只股票交易中学到的模式可以推广到另一只股票。

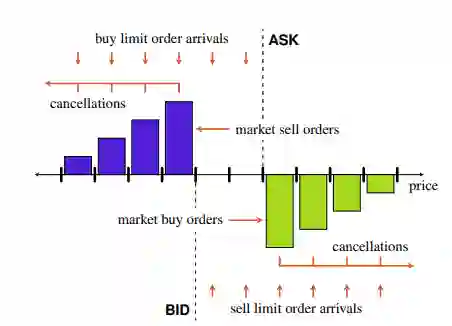
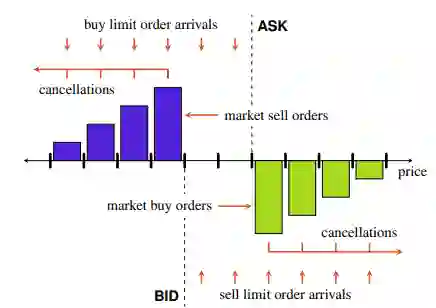
图2.1: 按不同价格水平提交限价订单。卖出价高于买入价。最低卖出价和最高买入价之间的差别就是买卖价差。中间价是最好的卖出价和最好的出价的平均值。

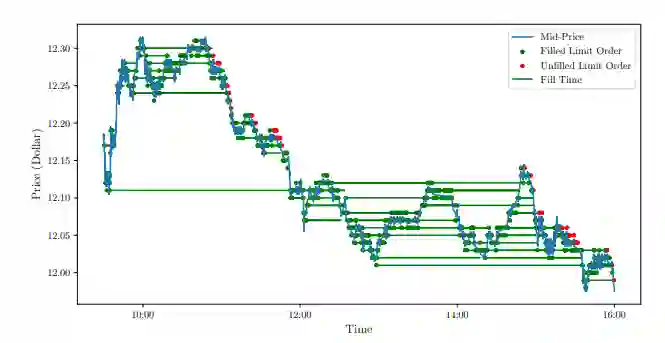
图 2.4：蓝线是一天中 BOA 股票的中间价。每个合成限价单在提交时由一个点表示。点根据其执行结果着色：如果限价单在一天结束时被执行，则它被着色为绿色；否则它是红色的。对于任何已成交的特定订单，一条水平线将其提交时间和执行时间连接起来——线的长度表示成交时间。

在论文的最后一部分，我们考虑了高维资产收益的协方差矩阵的估计问题。传统的方法之一是利用线性因子模型及其主成分分析估计。在本章中，我们使用变分自动编码器将线性因子模型推广到非线性因子模型的一般框架。我们证明了线性因子模型等价于一类线性变分自编码器。此外，非线性变分自编码器可以通过放宽线性假设来扩展到线性因子模型。协方差估计的一个应用是构造最小方差投资组合。通过数值实验，我们证明了变分自编码器在线性因子模型的基础上进行了改进，得到了更优的最小方差组合。

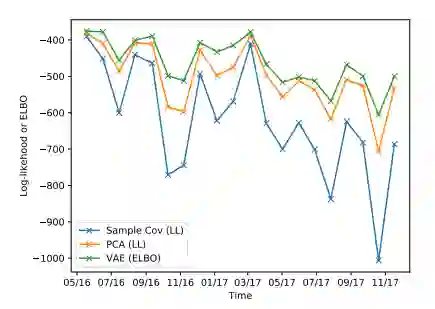
图4.1: 协方差矩阵估计比较