生成式人工智能的扩散模型概述

本文提供了对去噪扩散概率模型（DDPMs）的数学严谨介绍，DDPMs 有时也被称为扩散概率模型或扩散模型，主要用于生成式人工智能。我们提供了 DDPMs 的基本数学框架，并解释了训练和生成过程背后的主要思想。本文还回顾了文献中一些选定的扩展和改进，如改进版 DDPMs、去噪扩散隐式模型、无分类器扩散引导模型以及潜在扩散模型。

1 引言

生成模型的目标是基于从未知潜在分布中采样得到的数据集，生成新的数据样本。为了实现这一目标，已经提出了许多不同的机器学习方法，例如生成对抗网络（GANs）[12]、变分自编码器（VAEs）[22]、自回归模型[47]、归一化流[37]和能量基模型[25]。本文将介绍去噪扩散概率模型（DDPMs），这是一类生成方法（有时也被称为扩散模型或扩散概率模型），其基于重建一个扩散过程的思想，扩散过程从潜在分布开始，逐渐向其状态添加噪声，直到最终状态完全是噪声，然后反向重建。通过这种反向重建，纯噪声转变为有意义的数据，因此 DDPMs 提供了一种自然的生成框架。我们旨在提供对 DDPMs 背后动机思想的基本但严谨的理解，并对文献中一些最具影响力的基于 DDPM 的方法进行精确描述。

DDPMs 最初在 [44] 中提出，并在 [15] 中进一步推广，已经能够在图像合成和编辑 [31,35,36,38,40]、视频生成 [17,53]、自然语言处理 [3,26] 和异常检测 [50,52] 等许多领域取得最先进的成果。在经典的形式中，DDPM 是一个由两个随机过程组成的框架，即正向过程和反向过程。正向过程——扩散过程——从初始时间步骤的（近似）潜在分布开始（例如，它的初始状态可以是数据集中的随机样本），然后逐渐向其状态添加噪声，直到其终止时间步骤的状态（近似）完全是噪声。反向过程——去噪过程——是一个参数化过程，从（终止时间步骤）完全噪声的状态开始。在 DDPM 的背景下，关键思想是学习反向过程的参数，使得反向过程每个时间步骤的分布近似与正向过程对应时间步骤的分布相同。如果这一目标得以实现，反向过程可以解释为逐渐去除噪声，直到恢复到正向过程的初始分布。从这个意义上讲，反向过程逐渐去噪其完全噪声的初始状态。一旦找到合适的反向过程参数，生成过程便是从反向过程采样生成的。 在第2节中，我们将为 DDPMs 构建一个一般的数学框架，并解释反向过程的训练和生成样本的基本思想。接着，在第3节中，我们将考虑该框架的最常见特例，即噪声为高斯噪声，反向过程由去噪人工神经网络（ANN）控制的情况。在第4节，我们将讨论文献中用于评估生成样本质量的一些指标。最后，在第5节中，我们将讨论一些文献中提出的最流行的基于 DDPM 的方法，如改进版 DDPMs（见 [15]）、去噪扩散隐式模型（DDIMs）（见 [45]）、无分类器扩散引导模型（见 [16]）以及潜在扩散模型（见 [38]）。特别是，无分类器扩散引导模型和潜在扩散模型展示了如何引导反向过程生成来自不同类别的数据以及基于给定文本生成数据。 本文的支持代码可在 https://github.com/deeplearningmethods/diffusion_model 获得。

2 去噪扩散概率模型（DDPMs）

在本节中，我们将介绍去噪扩散概率模型（DDPMs）的主要思想。具体来说，我们将首先介绍并讨论DDPMs的一般数学框架，并在2.1小节中详细阐述其一些基本性质；接着，我们将在2.2小节中讨论DDPMs的训练目标，分析其如何实现生成建模的目标；最后，在2.3小节中，我们将基于这一训练目标，提出一种简化的DDPM方法。

3 带有高斯噪声的DDPMs

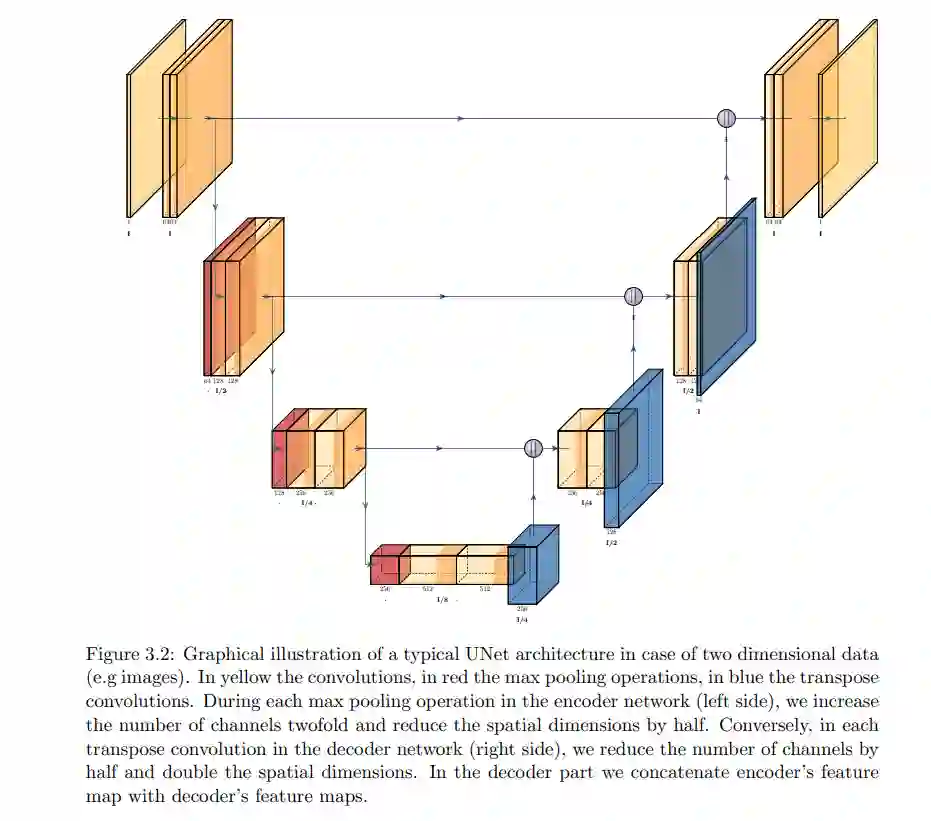
在本节中，我们考虑在转移核由高斯分布给出时，带有马尔可夫假设的DDPMs。本节中考虑的设置和方法基本上与[15]中提出的相对应。直观而言，在这个设置中，我们认为正向过程逐渐向训练样本添加高斯噪声，反向过程则旨在逐渐去除噪声，从而恢复原始的训练样本。 我们首先在3.1小节中讨论高斯分布的一些基本性质。然后，在3.2小节中，我们介绍并描述一个涉及高斯分布作为转移核的DDPM框架。接着，在3.3小节中，我们讨论这种转移核选择对正向过程分布的影响，并在3.4小节中探讨此选择对上述引理2.9中训练目标的上界的影响。受到前述章节启发，我们在3.5小节中描述了带有高斯噪声的DDPM的训练和生成方案。最后，在3.6小节中，我们指出了一些可能的人工神经网络（ANNs）架构选择，这些架构出现在3.5小节方法描述中。

4 生成模型的评估

在生成建模的背景下，特别是在扩散模型中，评估生成数据的质量和性能是至关重要的。因此，找到稳健的评估指标对于确保模型能够生成期望的结果至关重要。在本节中，我们考虑了用于这一目的的两类指标：内容变异指标和内容不变指标。这些指标提供了对模型在不同方面能力的理解。在4.1小节中，我们详细解释了两种内容不变指标：生成模型评估指标（Inception Score，IS）和Fréchet生成模型距离（Fréchet Inception Distance，FID）；在4.2小节中，我们概述了最常用的内容不变评估指标。