【CIKM2025教程】用于连续时间分析的神经微分方程

概述

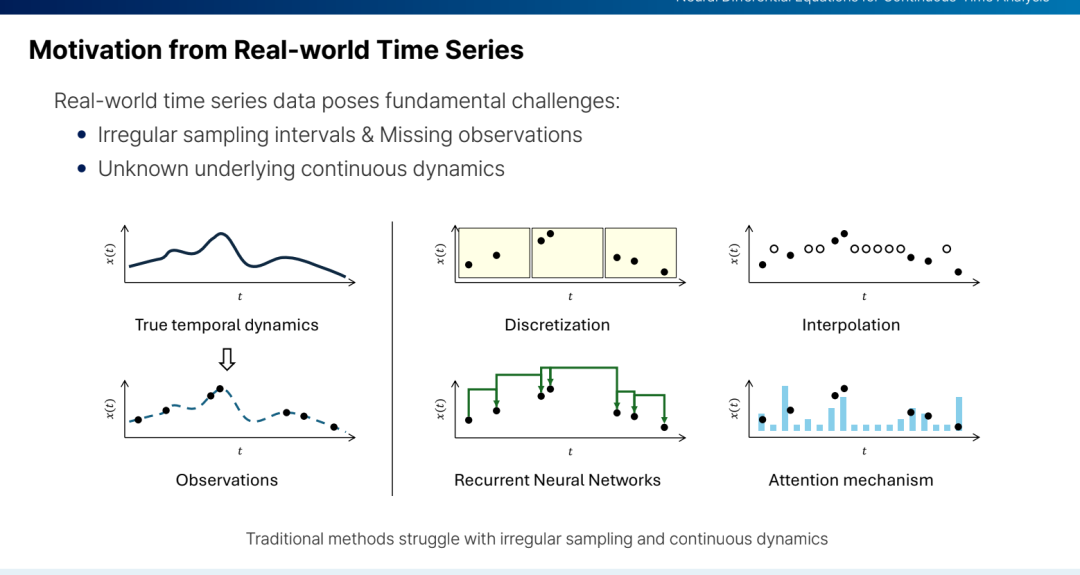
对复杂且不规则的时间序列进行建模是知识发现与数据挖掘中的一项关键挑战。本教程介绍神经微分方程（Neural Differential Equations, NDEs）——一种强大的连续时间深度学习范式，它能够在传统模型易受影响的情形下（如非均匀采样与缺失值）进行内在而自然的处理。我们对整个 NDE 家族进行了系统性的理论与实践回顾，包括：神经常微分方程（Neural ODEs, NODEs）、神经受控微分方程（Neural CDEs, NCDEs）以及神经随机微分方程（Neural SDEs, NSDEs）。本教程特别强调鲁棒性与稳定性，并在最后提供一个动手实践环节，参与者将使用关键的开源库解决插值与分类等真实任务。本教程面向 AI 研究者与应用工程师，帮助他们掌握时间序列分析的核心工具。

---

学习目标

在完成本教程后，你将能够： * 理解为何连续时间建模对于不规则与多分辨率时间序列具有优势。 * 掌握 NODEs、NCDEs 与 NSDEs 之间的差异 —— 包括它们的建模假设、优势与局限。 * 能够在关注求解器选择、稳定性与计算成本的前提下，训练并评估基于 NDE 的模型。 * 了解在敏感领域中提升模型鲁棒性、可解释性与可信度的策略。

---

目标受众

进入时间序列建模领域的研究生。 * 从事具有不规则或稀疏观测数据的应用研究人员。 * 在数据分布偏移与存在不确定性的场景中，寻求鲁棒预测或分类方案的实践者。

先修要求：

熟悉微积分、线性代数与概率论。 * 熟悉深度学习基础与 PyTorch。

---

教程结构与内容安排

Session I：连续时间建模基础 〔链接〕

概述与动机（10 分钟）

为什么是连续时间？不规则数据带来的挑战。 * 神经常微分方程（35 分钟）

理论、核心概念，以及用于训练的伴随方法（adjoint method）。 * 动手实践：第一部分〔链接〕（30 分钟）

实现 Neural ODEs 与 Latent ODEs。

---

Session II：高级模型与应用 〔链接〕

神经受控微分方程（25 分钟）

将不规则数据视为连续路径进行处理。 * 神经随机微分方程（20 分钟）

建模不确定性；重点介绍稳定 SDE（Stable SDEs）。 * 动手实践：第二部分〔链接〕（20 分钟）

实现并比较高级模型。

---

总结与未来方向（10 分钟）

**

**

https://nde-for-ts.github.io/tutorial/