本文研究的是军事行动中动态作战规划的双人零和随机博弈模型。在每个阶段,博弈者都要管理多个指挥官,这些指挥官要对具有开放控制线的目标下令采取军事行动。当发生争夺目标控制权的战斗时,其随机结果取决于其他目标控制权所提供的行动和有利支持。每个玩家的目标都是最大限度地增加他们所控制目标的累计数量,并根据其关键性进行加权。为了解决这个大规模随机博弈,我们利用后勤和军事行动指挥与控制结构,推导出其马尔可夫完美均衡的属性。我们证明了最优价值函数相对于部分有序状态空间的等调性,这反过来又导致了状态和行动空间的显著缩小。我们还通过消除受支配的行动和研究每次迭代求解的矩阵博弈的纯均衡来加速沙普利值迭代算法。我们在一个案例研究中展示了均衡结果的计算价值,该案例研究反映了具有地缘政治影响的代表性作战级军事战役。我们的分析揭示了均衡状态下博弈参数和动态之间复杂的相互作用,为战役分析人员提供了新的军事见解。
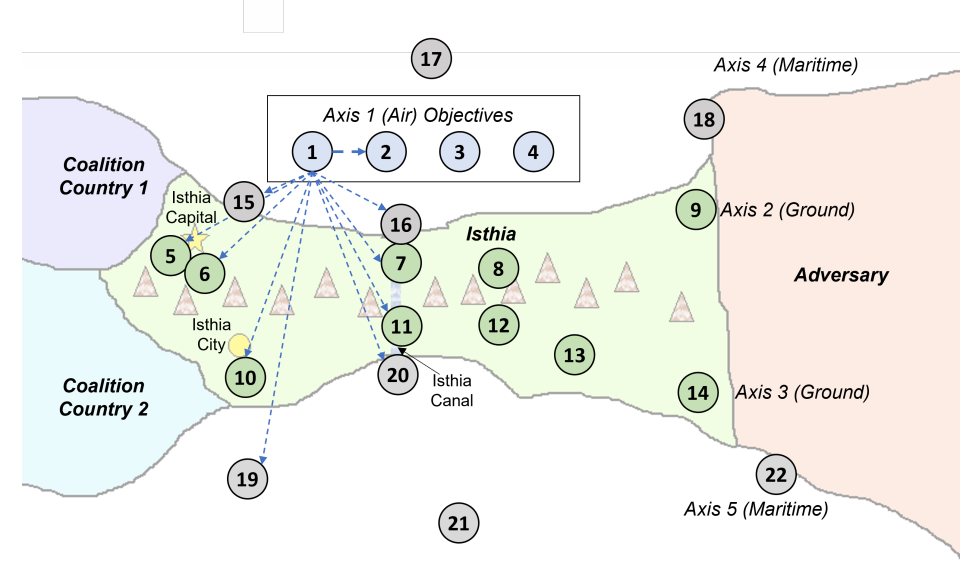
图 6 战役地理和目标。说明玩家 1 控制综合防空系统(目标 1)的效果:控制目标 1 是成功实现空域 1(目标 2)的必要条件,同时也增加了成功夺取目标 5、6、7、10、11、15、16、19 和 20 的可能性。
在激烈竞争时期,军事领导层对国家的安全起着不可或缺的作用。理想情况下,领导层可以继续阻止对手将战争升级为动能战争(HQDA 2021);然而,为武装冲突制定规划至关重要。日益加剧的地缘政治动荡表明,大国之间发生动武战争的可能性越来越大(Garamone 2022)。2022 年 2 月升级为公开武装冲突的俄乌战争就是明证。在这种全球背景下,高级军事领导层及其参谋人员必须继续开展战术、作战和战略层面的统一规划,以支持国家安全目标(JCS 2020)。
作战层面的战争将部队的战术运用与国家战略目标联系起来(JCS 2017)。在这一层面,联合部队指挥官领导各组成部分指挥官(如空中、陆地和海上)打击冲突。一连串的行动和战斗构成了一场军事战役(Lynes 等人,2014 年),战略家、规划人员和分析人员都会对其进行分析,为高级军事领导层推荐作战规划并提出地缘政治见解(Mueller,2016 年;Shlapak & Johnson,2016 年;Flanagan 等人,2019 年;Mazarr 等人,2019 年)。
然而,分析军事战役的主要挑战来自其内在的不确定性(Tecott & Halterman 2021),这种不确定性来自三个方面:对手的规划、军事行动的相互关联性以及战争的动态流程。由于对手的规划是未知的,在复杂的作战环境中(JCS 2020),战斗的结果也是不确定的。要在相互关联的指挥官之间同步开展行动,就需要联合规划、沟通和协调,以统一行动(JCS 2017)。最后,军事行动的动态流程导致了潜在战役之间过渡的不确定性。例如,在第二次世界大战期间,盟军成功的 D-Day 入侵最终导致了 "市场花园行动"(Operation Market Garden),而美国和英国的挫折导致苏联军队首先到达柏林(普鲁特,2019 年)。这种动态性要求必须考虑未来的不确定结果,以优化当前的决策。
现有的战役分析方法包括兵棋推演和战斗模拟(Turnitsa 等人,2022 年)。这些工具虽然有效,但并不考虑军事战役的不确定性或行为动态,而且需要大量的时间和资源。此外,为控制军事目标而分配资源的博弈论模型并不考虑关键的战役方面,包括军事战役的动态性、顺序性、供应链要求或军事指挥结构(Washburn,2014 年)。我们希望用一种更快的技术来增强当前的方法,这种技术可以扩展到对许多输入进行评估,这就提出了我们的研究问题: 我们该如何设计动态军事行动规划,并为高层领导提供及时的评估和见解?
为了解决这一研究问题,我们在 Haywood(1954 年)的静态博弈模型的基础上,提出了一种新颖的双人、贴现、零和、随机博弈模型,用于军事战役中的动态作战规划。该模型的特点考虑到了关键的军事特征,如多名指挥官的协调、对既定补给线的需求以及取决于对附近目标控制的战斗结果的随机性。
通过利用后勤和军事行动指挥与控制结构,我们得出了博弈的马尔可夫完美均衡所满足的属性。在符合实际的假设条件下,我们证明了最优价值函数相对于部分有序状态空间的结果等调性(定理 1)。这一主要结果以及博弈论的论证使我们能够确定可实现状态的集合以及均衡状态下政策剖面的属性(命题 1)。这些特性大大缩小了状态和行动空间,从而使我们能够使用沙普利值迭代算法来解决这个大型博弈。
在只有一个指挥官的战役特例中,我们进一步证明,在价值迭代算法的大多数状态下求解的矩阵博弈都承认弱支配策略,甚至在指挥官管理单一目标轴时承认纯均衡(命题 2)。这些结构性结果促使我们设计了一种加速价值迭代算法(算法 1-2),该算法可在使用线性规划求解矩阵博弈之前搜索纯均衡或消除弱支配行动。
然后,我们根据虚构的地缘政治场景设计了一个具有代表性的案例研究。我们分析并比较了博弈者在不同均衡状态下的混合策略,并强调了一种复杂的行为,这种行为取决于目标的临界度、目标之间的概率相互依赖关系以及博弈的动态性。我们还表明,战略投资决策必须谨慎选择时机,因为它们对博弈在不同初始状态下的最优值有不同的影响。最后,我们的均衡结果允许我们使用我们的加速值迭代算法来求解所有考虑过的军事战役的随机博弈,与经典的值迭代算法相比,该算法的运行时间缩短了 72%。我们的分析为军事领导层提供了新颖的作战见解。
本文其余部分安排如下:第 2 节简要讨论了军事战役分析和当前工具。然后回顾了与军事领域相关的现有随机博弈文献。我们在第 3 节阐述了随机博弈。然后,我们推导出均衡结果,并在第 4 节介绍我们的加速值迭代算法。在第 5 节中,我们介绍了计算结果和案例研究中的军事见解。第 6 节是结束语和未来研究方向。最后,我们的结果的数学证明载于附录 A。
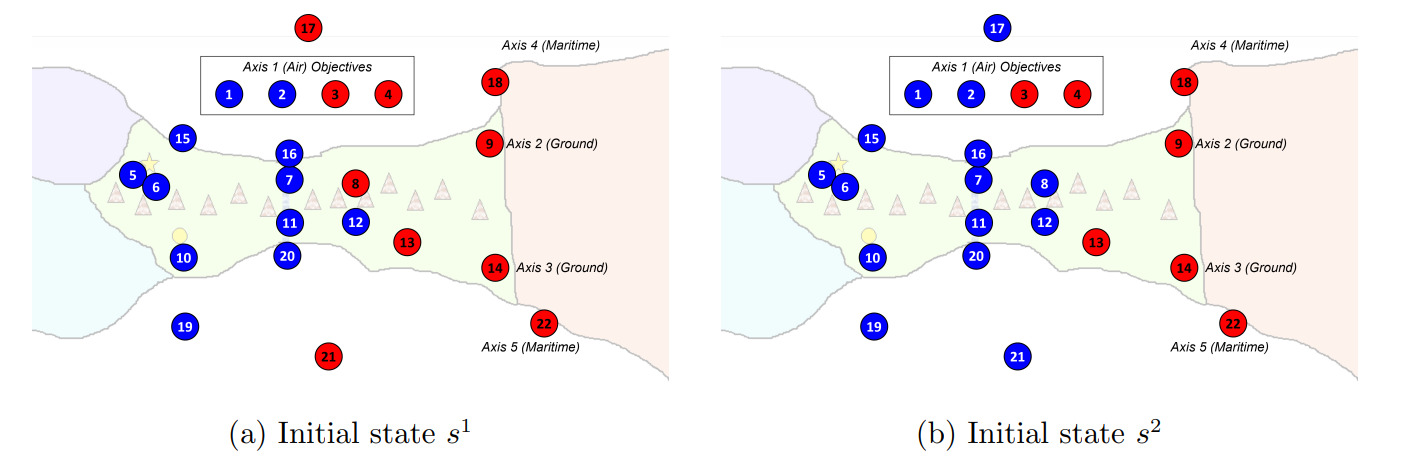
图 9 战役初始状态。联盟(或对手)控制的目标为蓝色(或红色)。