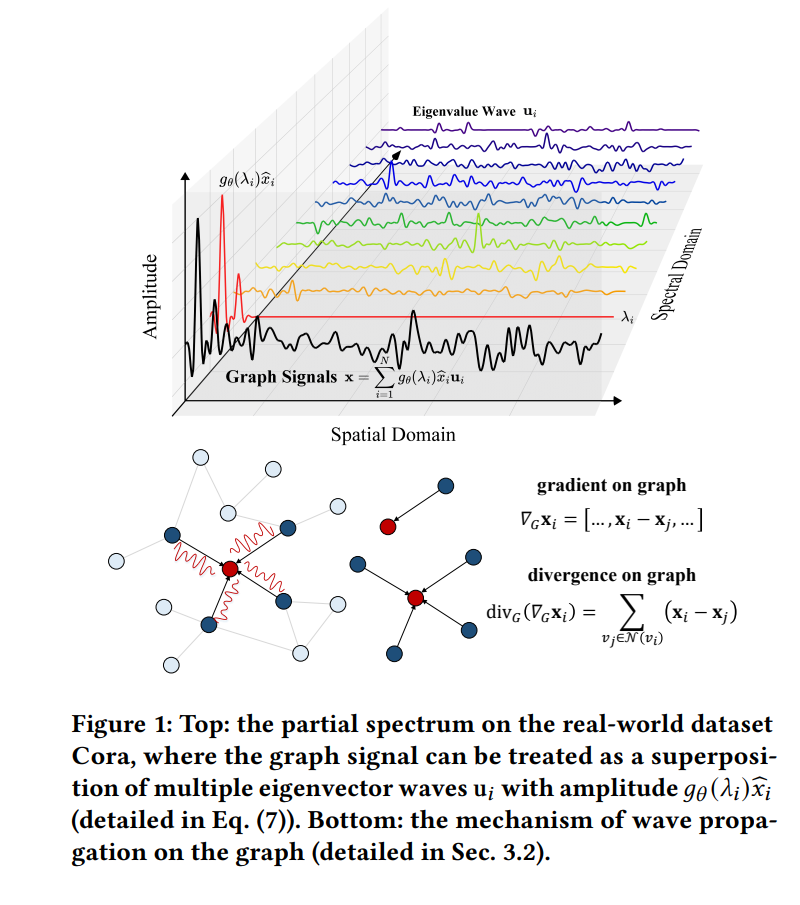
动态图建模被引入图神经网络(GNN)中的消息传递(Message Passing, MP)过程,作为一种新颖的建模范式。现有方法通常将节点之间的消息传递视为热扩散过程,并利用热传导方程来刻画嵌入空间中节点表示的时间演化。然而,在图信号处理中,热传导方程难以描述图信号所具有的波动特性。此外,热传导方程本质上是一阶时间偏导的偏微分方程(PDE),其数值解往往稳定性较差,导致模型训练效率较低。 本文旨在在消息传递中更充分地刻画图信号的波动特性,因为图信号本质上是波信号,可以视为一系列以特征向量形式存在的波的叠加。这一观察促使我们将消息传递过程建模为波传播过程,以捕捉空间中波信号的时间演化特性。基于物理学中的波动方程,我们创新性地提出图波动方程(Graph Wave Equation),用于刻画图上的波传播行为。
具体而言,我们展示了图波动方程与传统谱域图神经网络(Spectral GNN)之间的关联,从而为基于不同拉普拉斯算子的**图小波网络(Graph Wave Networks, GWNs)**设计提供了理论基础,并增强了谱域GNN的性能。此外,图波动方程是一个涉及二阶时间偏导的偏微分方程,相比涉及一阶时间偏导的热传导方程,其在图结构中具有更强的数值稳定性。我们还从理论上证明了基于图波动方程所得的数值解具有持续的稳定性,从而在保证模型性能的同时显著提升了训练效率。 大量实验证明,GWNs 在多个基准数据集上实现了高效且领先的性能表现,并在处理图神经网络中的关键挑战(如过度平滑和异质性)时展现出卓越的表现。我们的代码已开源,地址为:https://github.com/YueAWu/Graph-Wave-Networks。
成为VIP会员查看完整内容
相关内容
Arxiv
213+阅读 · 2023年4月7日