【DeepMind-NeurIPS 2020】元训练代理实现Bayes-optimal代理

基于记忆的元学习是一种强大的技术，可以构建能够快速适应目标分布中的任何任务的agents。之前的一项理论研究认为，这种显著的表现是因为元训练方案激励agent以贝叶斯最优的方式行为。我们通过一些预测和敲诈任务对这一主张进行了实证研究。在理论计算机科学的启发下，我们发现元学习和贝叶斯最优agent不仅行为相似，而且在某种意义上，它们甚至共享相似的计算结构，即一个agent系统可以近似地模拟另一个。此外，我们证明贝叶斯最优agent是元学习动态的不动点。我们的研究结果表明，基于记忆的元学习可以作为一种通用技术，用于数值逼近贝叶斯最优agent，也就是说，甚至对于我们目前没有可处理模型的任务分布也是如此。

在“学习到学习”的范式中，基于记忆的元学习是一种创建代理的强大技术，它能快速适应从目标分布中抽取的任何任务。此外，有人声称元学习可能是创建泛化到看不见的环境的系统的关键工具。计算神经科学的研究也部分支持了这一观点，其中对人类的实验研究表明，快速的技能适应依赖于任务的变化。因此，理解元学习agent如何获得它们的表征结构并执行它们的计算是至关重要的，因为它可以为架构选择、训练任务的设计提供信息，并解决人工智能中的泛化和安全性问题。

以前的理论工作认为，充分优化元学习目标的agent是通过构造的贝叶斯最优，因为元学习目标是贝叶斯最优目标的蒙特卡罗近似。这是令人震惊的，因为贝叶斯最优agent通过最优地权衡勘探和开发来实现收益最大化(或损失最小化)。该理论还提出了一个更强的、结构化的主张:即经过元训练的agent在幕后执行贝叶斯更新，其中计算是通过嵌入在内存动态中的状态机实现的，该状态机跟踪解决任务类所需的不确定性的充分统计信息。

在这里，我们着手实证综述元学习agent的计算结构。然而，这带来了不小的挑战。人工神经网络以其难以解释的计算结构而臭名昭著:它们在具有挑战性的任务中取得了卓越的表现，但这种表现背后的计算仍然难以捉摸。因此，尽管可解释机器学习的许多工作集中在I/O行为或记忆内容上，只有少数通过仔细的定制分析来研究引起它们的内部动态(见例[12 18])。

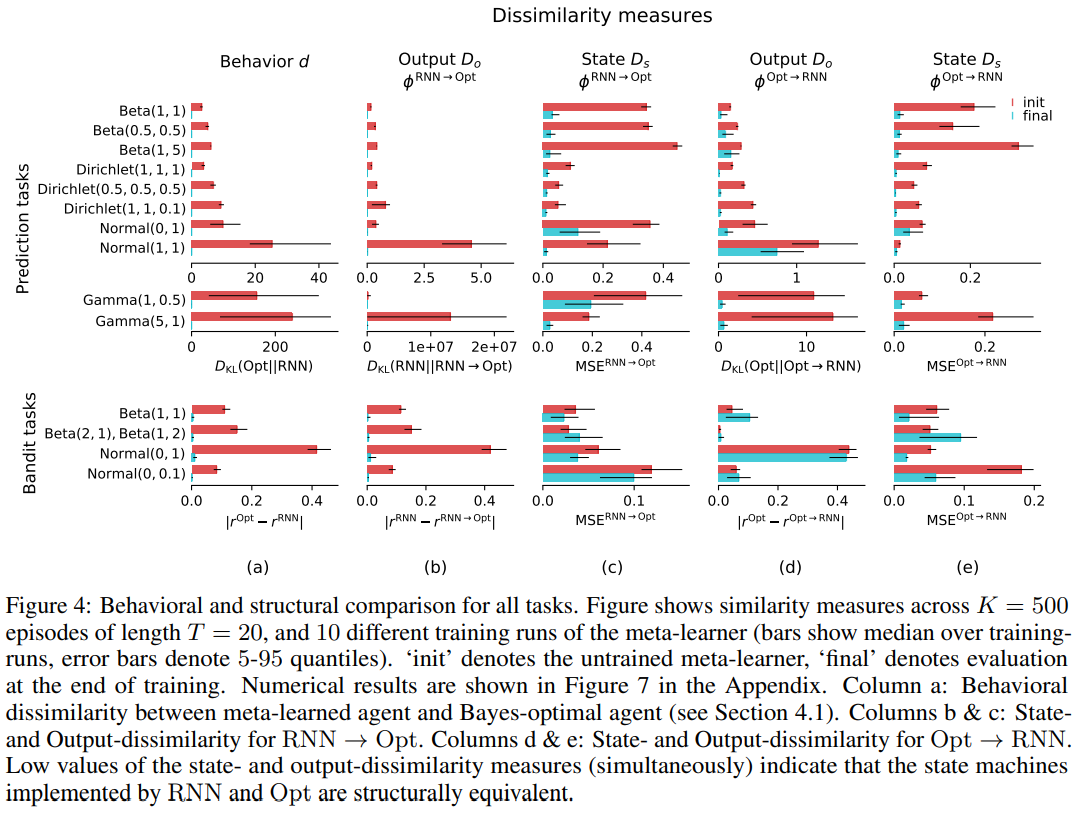
为了应对这些挑战，我们调整了理论计算机科学与机器学习系统的关系。具体来说，为了在计算级别[19]上比较agent，我们验证它们是否可以近似地相互模拟。仿真的质量可以根据原始和仿真之间的状态和输出相似度来评估。

因此，我们的主要贡献是研究基于RNN的元学习解决方案的计算结构。具体地说，我们比较元学习代理的计算和贝叶斯最优agent的计算，在他们的行为和内部表示的一套预测和强化学习任务已知的最优解决方案。我们在这些任务中展示了这一点:

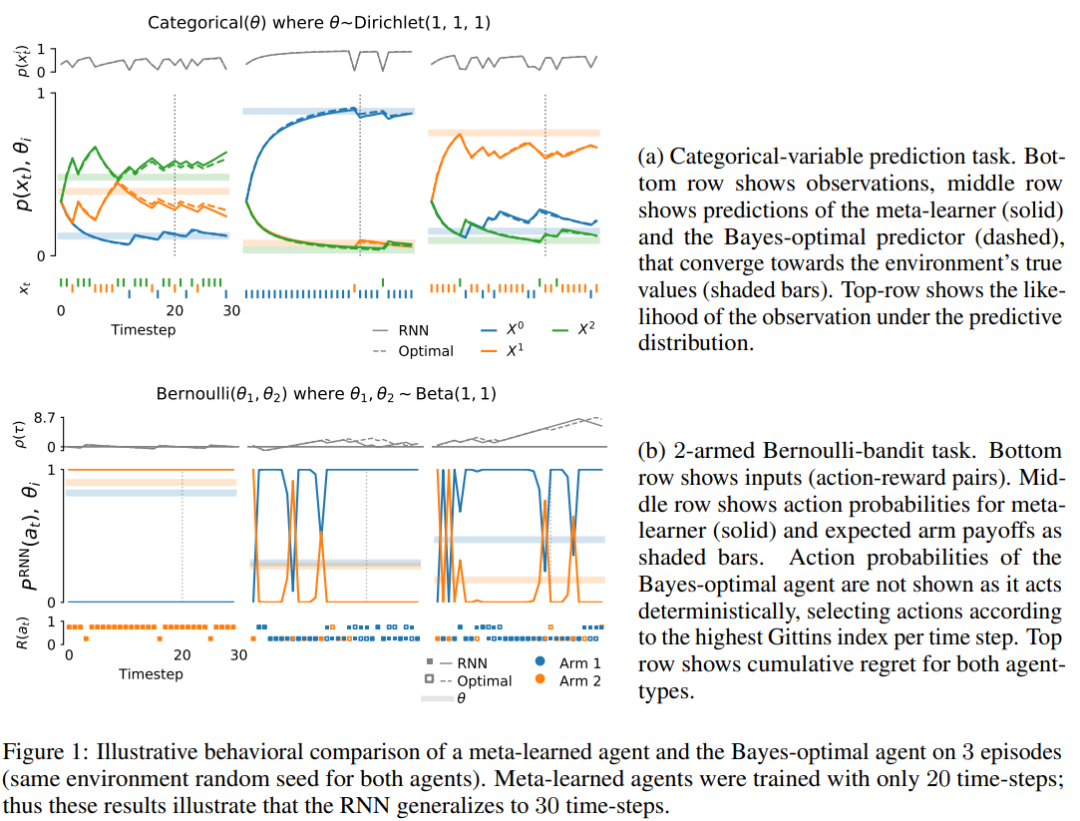
• 元学习代理的行为类似贝叶斯最优agent(第4.1节)。也就是说，元学习agent做出的预测和行动实际上与贝叶斯最优agent无法区分。

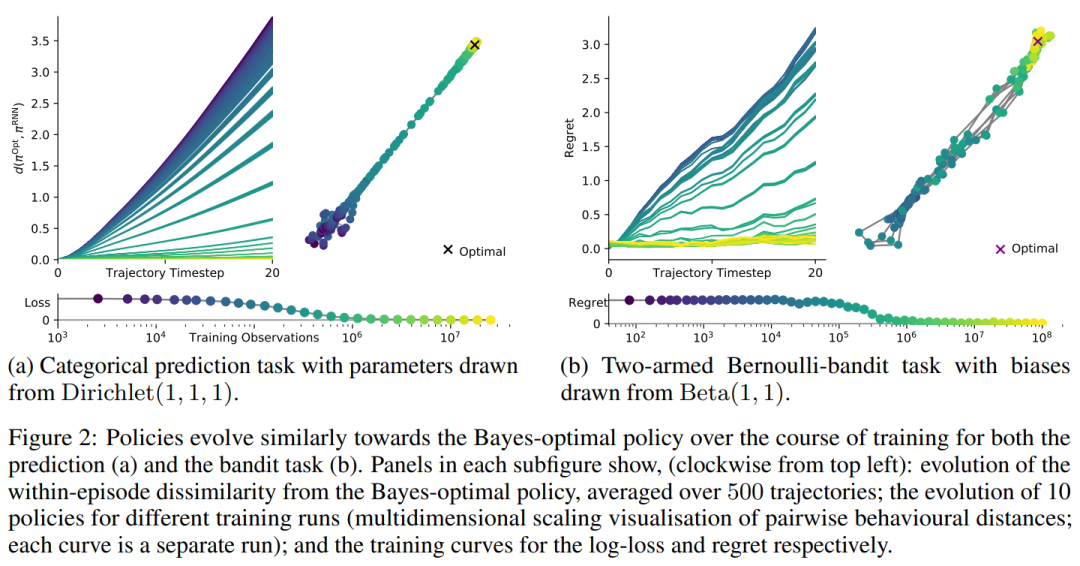
• 在元训练过程中，元学习者收敛于贝叶斯最优(第4.2节)。我们的经验表明，贝叶斯最优策略是学习动态的不动点。

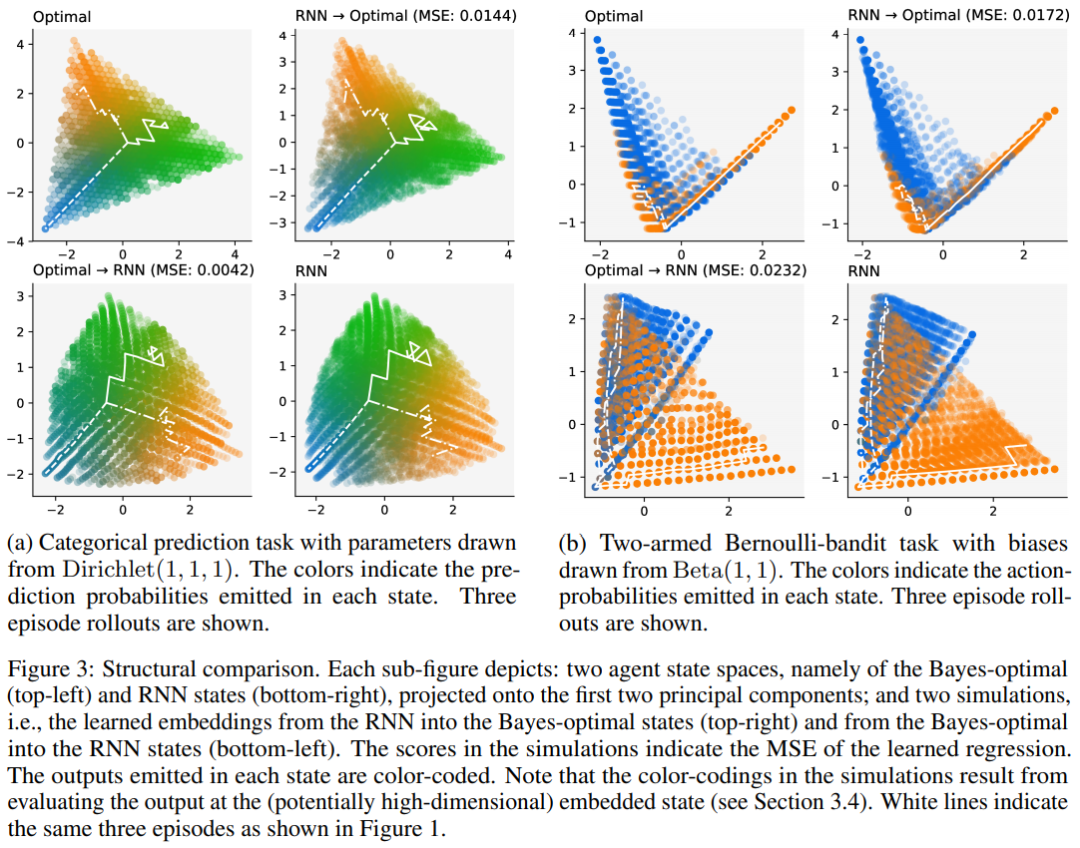
• 元学习代理代表像Bayes-optimal代理这样的任务(第4.3节)。具体来说，计算结构对应于嵌入在(欧几里得)内存空间中的状态机，其中状态编码任务的充分统计信息并产生最优操作。我们可以用贝叶斯最优agent执行的计算来近似地模拟元学习代理执行的计算。