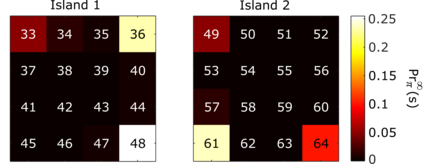
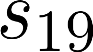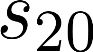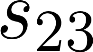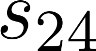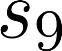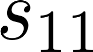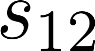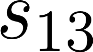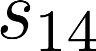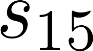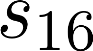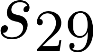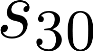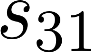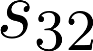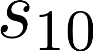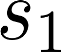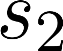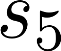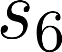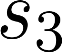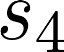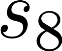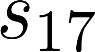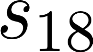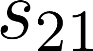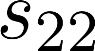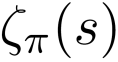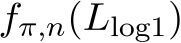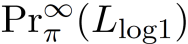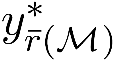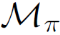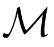The planning domain has experienced increased interest in the formal synthesis of decision-making policies. This formal synthesis typically entails finding a policy which satisfies formal specifications in the form of some well-defined logic, such as Linear Temporal Logic (LTL) or Computation Tree Logic (CTL), among others. While such logics are very powerful and expressive in their capacity to capture desirable agent behavior, their value is limited when deriving decision-making policies which satisfy certain types of asymptotic behavior. In particular, we are interested in specifying constraints on the steady-state behavior of an agent, which captures the proportion of time an agent spends in each state as it interacts for an indefinite period of time with its environment. This is sometimes called the average or expected behavior of the agent. In this paper, we explore the steady-state planning problem of deriving a decision-making policy for an agent such that constraints on its steady-state behavior are satisfied. A linear programming solution for the general case of multichain Markov Decision Processes (MDPs) is proposed and we prove that optimal solutions to the proposed programs yield stationary policies with rigorous guarantees of behavior.
翻译:规划领域对决策政策的正式综合越来越感兴趣。这种正式综合通常需要找到一种政策,这种政策以某种明确界定的逻辑形式,例如线性时空逻辑(LTL)或计算树逻辑(CTL)等形式,满足正式的规格。这种逻辑非常有力,表现了它们捕捉理想代理人行为的能力,但当制定满足某些类型无症状行为的决策政策时,其价值是有限的。特别是,我们想具体说明一个代理人的稳定状态行为受到的限制,它捕捉到一个代理人在每一州与它的环境进行无限期互动的时间比例。这有时被称为代理人的平均或预期行为。在本文中,我们探讨了为一个代理人制定决策政策的稳定状态规划问题,例如对其稳定状态行为的限制得到了满足。对于多链式马尔科夫决定程序(MDPs)的一般情况,我们提出了线性方案编制解决办法,并证明拟议方案收益率政策的最佳解决办法是严格保证行为。