对比预训练和多模态生成式人工智能的统计理论

多模态生成式人工智能系统，例如结合视觉和语言的系统，依赖对比预训练来学习不同模态之间的表示。尽管它们的实际应用价值得到了广泛认可，但对对比预训练框架的严格理论理解仍然有限。本文发展了一个理论框架，用以解释对比预训练在下游任务中的成功，例如零-shot分类、条件扩散模型和视觉-语言模型。我们引入了近似充分统计量的概念，这是经典充分统计量的推广，并证明了对比预训练损失的近似最小化解是近似充分的，这使得它们能够适应不同的下游任务。我们进一步提出了联合生成层次模型，用于描述图像和文本的联合分布，表明变换器可以通过信念传播高效地逼近该模型中的相关函数。基于这个框架，我们推导出了基于对比预训练表示的多模态学习的样本复杂度保证。数值仿真验证了这些理论发现，证明了对比预训练变换器在各种多模态任务中的强大泛化能力。

1. 引言

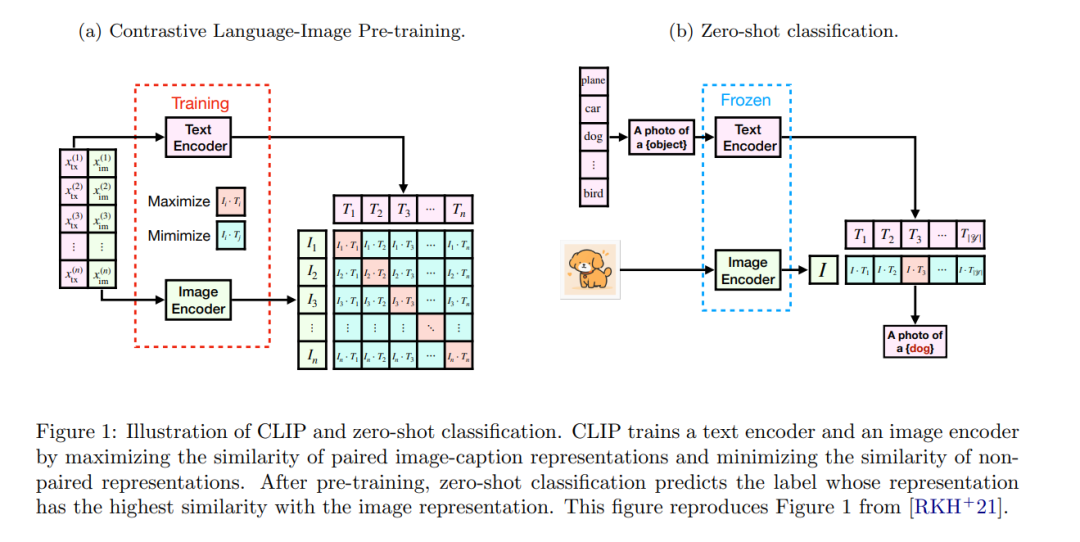
多模态生成式人工智能系统，如用于从文本提示生成图像的DALL-E [Ope22]，以及用于基于图像和文本输入生成文本的GPT-4V [Ope23]，已取得了显著的实证成功。这类系统的训练过程通常从对比预训练 [RKH21, JYX21] 开始，使用大规模预训练数据集为每种模态学习低维神经网络表示。随后，固定一个模态的对比预训练表示，并用于引导另一个模态生成模型的训练。为了详细说明，我们专注于图像-文本领域的多模态学习，在该领域，对比预训练过程被称为对比语言-图像预训练（CLIP）[RKH`21]。给定一组配对的图像-文本样本(xim,xtx)∈Xim×Xtx(x_{\text{im}}, x_{\text{tx}}) \in X_{\text{im}} \times X_{\text{tx}}(xim,xtx)∈Xim×Xtx，CLIP训练一对神经网络编码器(Eim:Xim→Rp,Etx:Xtx→Rp)(E_{\text{im}}: X_{\text{im}} \to \mathbb{R}^p, E_{\text{tx}}: X_{\text{tx}} \to \mathbb{R}^p)(Eim:Xim→Rp,Etx:Xtx→Rp)，通过对配对的图像-文本进行对齐，同时将未配对的图像-文本推得尽可能远。此对齐通过最小化在公式(2)中定义的对比损失来实现。预训练的CLIP编码器在各种下游任务中表现出色，包括：

零-shot分类 [RKH21, JYX21]：目标是为新的图像xim∈Ximx_{\text{im}} \in X_{\text{im}}xim∈Xim 预测标签y∈Yy \in Yy∈Y。使用预训练的编码器(Eim,Etx)(E_{\text{im}}, E_{\text{tx}})(Eim,Etx)，可以在不需要任务特定数据微调的情况下构建一个好的分类器。
条件扩散模型 [Ope22, EKB`24]：任务是从文本提示xtx∈Xtxx_{\text{tx}} \in X_{\text{tx}}xtx∈Xtx 生成图像xim∈Ximx_{\text{im}} \in X_{\text{im}}xim∈Xim。在这些模型中，文本嵌入Etx(xtx)E_{\text{tx}}(x_{\text{tx}})Etx(xtx) 用于条件去噪函数，训练过程中不直接引用原始文本提示。
视觉-语言模型 [LLXH22, LLLL24]：任务是从图像提示xim∈Ximx_{\text{im}} \in X_{\text{im}}xim∈Xim 生成文本xtx∈Xtxx_{\text{tx}} \in X_{\text{tx}}xtx∈Xtx。在这类模型中，图像嵌入Eim(xim)E_{\text{im}}(x_{\text{im}})Eim(xim) 用于自回归变换器，训练过程中不直接引用原始图像提示。

多模态学习的实证成功凸显了建立理论框架的必要性，以便更好地理解这一范式，理想情况下应置于统计学习理论的背景下。为了实现这一目标，必须解决两个关键的理论问题：

为什么CLIP编码器能成为下游任务的有效表示？ 对比损失最小化的统计性质在文献中已经得到了广泛研究 [SPA`19, TKH21a, TKH21b, HWGM21]。现有的研究通常利用对比损失的结构及其与下游任务的关系，表明学习到的表示的线性函数在这些设置中表现良好。然而，这些分析无法解释像零-shot分类这样的任务（无需微调），以及涉及条件扩散模型和视觉-语言模型的任务，在这些任务中，学习到的表示的线性函数不足以捕捉相关的函数。
为什么编码器和下游函数能够有效地被神经网络逼近？ 这个问题受到了相对较少的关注。尽管神经网络是通用的函数逼近器 [Bar93]，但在处理一般高维目标函数时，它们可能会遭遇维度灾难 [Bac17]。主要的理论挑战在于构建一个既可操作又切实可行的统计模型来描述图像-文本的联合分布。高斯假设虽然在数学上方便，但通常过于限制且不现实，而完全非参数化的方法可能会导致维度灾难。

本文解决了上述两个理论问题。在第3节中，我们揭示了CLIP损失的近似最小化解的一个出人意料的简单特性：它们是近似充分统计量的对，这是一种对经典充分统计量的推广。由于它们的近似充分性和数据处理不等式的直接影响，这些表示能够适应多种下游任务，包括零-shot分类、条件扩散模型和视觉-语言模型。此外，当数据的“标准表示”存在时，我们展示了如何通过简单的两层网络从任何CLIP损失的近似最小化解中恢复它。这使得CLIP表示能够有效地适应下游任务，其中标准表示作为充分统计量。在第4节中，我们将我们的通用框架应用于图像和文本联合分布的统计模型，该模型我们称之为联合生成层次模型（JGHM）。JGHM是一个图模型，由两个具有共享根节点的树构成，其中根节点捕捉高层次特征，叶节点表示观察到的图像或文本。我们展示了变换器 [Vas17] 可以通过逼近信念传播算法高效地逼近JGHM中的相关函数，从而突破维度灾难。基于这一见解，我们推导出了使用预训练CLIP表示的零-shot分类、条件扩散模型和视觉-语言模型等任务的端到端样本复杂度结果。第5节中，我们在模拟的JGHM框架下呈现了数值仿真。实验结果表明，使用Adam算法 [Kin14] 训练的变换器可以实现近似最优的最小化解，展现出强大的泛化能力。此外，分布外测试表明，Adam获得的最小化解与信念传播的行为高度一致，这是一个独立的有趣结果。