在经典的人工智能中,符号知识通常表示为图结构框架中的关系数据,即关系知识库(KBs)。关系知识库存在不完整性问题,许多研究致力于知识库的补全。一种流行的方法是将关系数据映射到低维向量空间中的连续表示,称为关系表示学习。这种方法有助于保持关系结构,从而能够有效地从嵌入空间推断缺失的知识。然而,现有方法使用纯向量嵌入,将每个关系对象(如实体、概念或关系)映射为向量空间中的一个简单点(通常在欧几里得空间R中)。尽管这些纯向量嵌入在捕捉对象相似性方面表现出色,但在捕捉关系数据中固有的各种离散和符号属性方面存在不足。
本论文超越了传统的向量嵌入,采用几何嵌入来更有效地捕捉关系结构和关系数据中潜在的离散语义。几何嵌入将数据对象映射为几何元素,如具有常负曲率的双曲空间中的点或欧几里得向量空间中的凸区域(如盒子、圆盘),从而更好地建模关系数据中的离散属性。具体而言,本论文引入了多种几何关系嵌入模型,能够捕捉:1)网络和知识图谱中的复杂结构模式,如层次结构和循环;2)知识图谱中的复杂关系/逻辑模式;3)本体中的逻辑结构和适用于约束机器学习模型输出的逻辑约束;4)实体与关系之间的高阶复杂关系。
我们从基准和真实世界数据集中获得的结果表明,几何关系嵌入在熟练捕捉关系数据中固有的离散、符号和结构属性方面表现出色,进而在各种关系推理任务中实现了性能提升。
1.1 背景、动机与挑战
表示学习在现代机器学习中起着至关重要的作用,能够为各种现实世界的数据(包括图像 [80]、词汇 [164] 和文档 [87])生成紧凑、连续、低维的表示。这些分布式表示有助于区分相关特征,同时忽略对象之间不相关的变化。它们成为了图像识别 [80]、文本分类 [164] 和疾病诊断 [87] 等多种机器学习任务中的有价值输入。
当前许多工作中占主导地位的方法是将对象映射到低维向量空间,通常表示为欧几里得空间中的 RdR^dRd。我们将这种表示称为纯向量嵌入。使用纯向量嵌入的基本原理是,它们能够通过向量空间中的成对距离或内积来保留对象之间的“相似性”。例如,来自相同类别的图像或在相似语言环境中出现的词汇会被映射到嵌入空间中“相近”的向量。
与现代机器学习中流行的方法不同,经典人工智能(如知识表示与推理 [101] 和统计关系学习 [141])依赖符号知识。符号知识通常表示为结构化和关系化的数据,描述实体和/或概念之间的语义关系。通常,这种表示形式为一组事实陈述,每个陈述描述了一个涉及两个或多个实体和/或类的语义关系的事实。此外,借助复杂的数学构造,符号知识还可以表示为一组逻辑陈述,每个陈述描述了涉及不同实体和/或概念的逻辑关系。这些事实和逻辑陈述共同形成了符号知识库,存储了特定领域的关系知识。符号知识在包括生物医学 [42, 143] 和智能系统 [157] 的各种应用中发挥着关键作用。
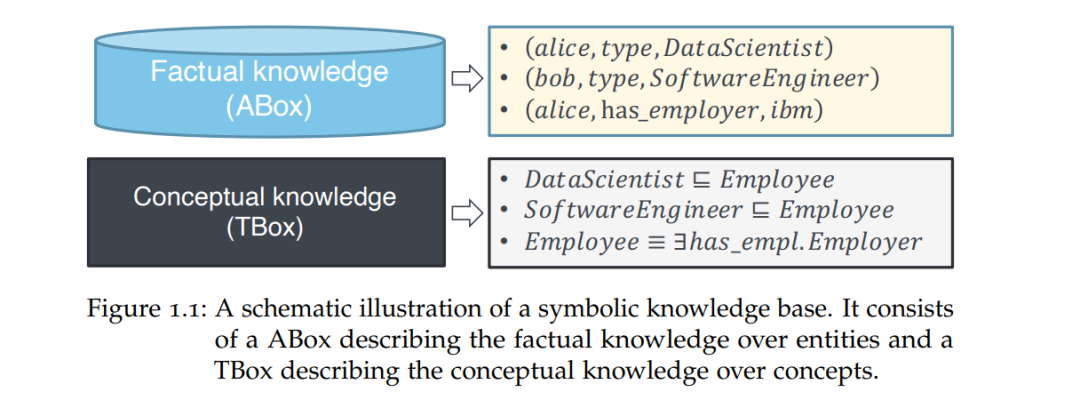
符号知识库中的关系知识可以分为两个类别,如图1.1所示: * 事实知识 描述了不同实体之间的关系。它通常以知识图谱的形式描述,事实知识通过三元组(h,r,t)表示,其中h和t是实体,r是它们之间的二元关系标签。除了二元关系之外,知识图谱还可以扩展以表示多个实体之间的高阶或多重关系,例如科学网络中的共同作者关系。 * 概念知识 描述了不同概念之间的关系。它通常在概念本体中描述,其中概念按照层次结构和概念关系(如“是...”、“有部分”)组织在一起。通过应用复杂的数学构造,如交集、存在量化和全称量化,本体还可以扩展为描述概念之间的逻辑关系。
根据语义网社区的惯例,我们将事实知识的部分称为ABox(断言性知识),而将概念知识的部分称为TBox(术语性知识)。
关系表示学习充当了桥梁,将离散和符号关系数据转化为连续的低维表示。这种方法将经典的知识表示与现代基于向量的机器学习相结合。使用向量表示关系数据的优势在于:1)向量表示不仅能够捕捉适合于经典推理的关系结构,还能捕捉实体/概念之间的相似性和类比结构,促进基于类比和相似性的推理。2)学习到的向量表示对不完整和噪声数据具有鲁棒性,使其更适合于现实世界场景中的推理任务。在现实世界中,许多关系数据集(如Freebase [16] 和DBpedia [6])是通过人工整理的。尽管这些数据量已经很大,但仍然是不完整和有噪声的。
向量表示已经在各种关系数据实例中证明了其效用,涵盖了图、知识图谱或多关系图谱以及本体: * 图嵌入 将图中的节点映射为向量,同时保留图结构 [91]。典型的方法包括基于随机游走的方法 [53] 和图神经网络 [30]。这些学习到的嵌入可以用于预测缺失的节点类型(即,节点分类)、节点之间的缺失边(即,链接预测)以及图的整体属性(即,图分类)。 * 知识或多关系图嵌入 将实体和关系都映射到向量空间,同时在嵌入空间中保留它们的关系结构 [89]。这是通过将实体之间的关系建模为函数(即,功能性方法)[19] 或通过将事实的可行性建模为三方交互(即,语义匹配方法)[130] 来实现的。知识图谱嵌入可以有效地推断缺失的关系事实,即使在不完整的知识图谱中,这一过程被称为知识图谱补全。 * 本体嵌入 将本体中的概念映射为向量,同时保留本体结构 [71]。与关注事实知识的知识图谱嵌入不同,本体嵌入主要考虑本体知识。将逻辑结构编码到标准嵌入空间中具有挑战性,但对于本体嵌入至关重要。
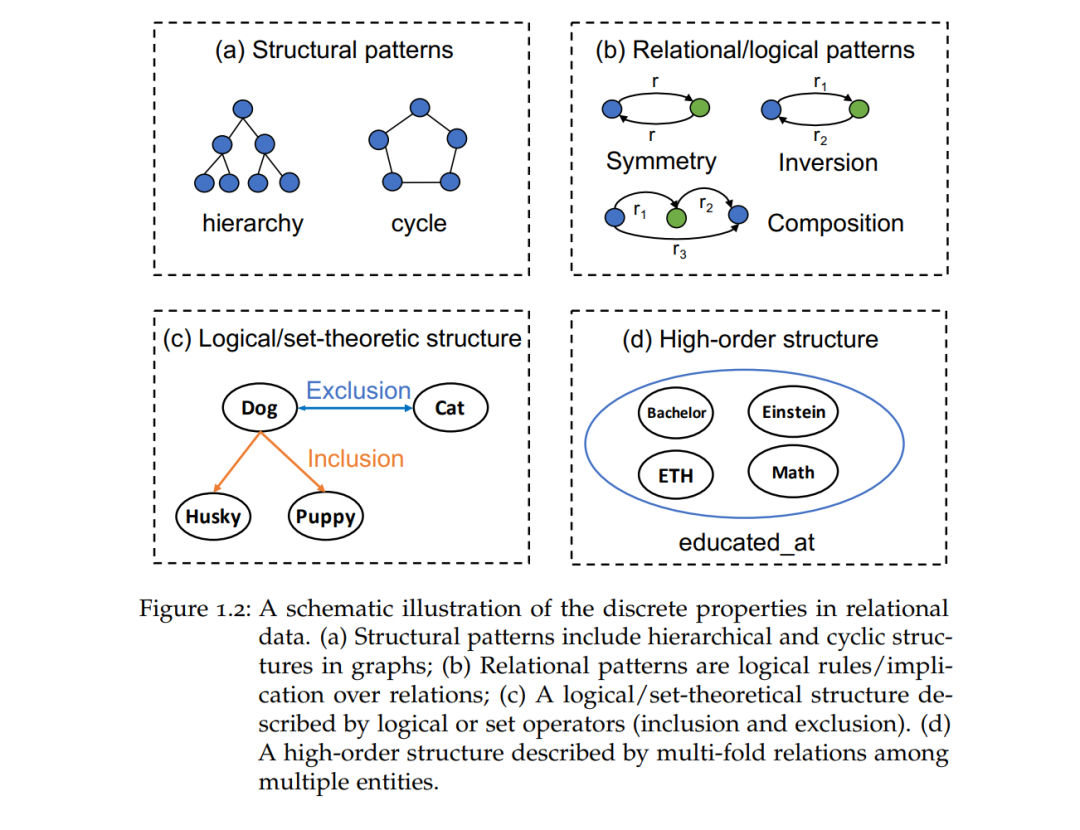
挑战:这些学习到的表示可以直接从嵌入空间中有效推理缺失的知识。然而,大多数关系表示学习方法将嵌入表示为简单的欧几里得向量,类似于图像和文本数据的嵌入,但它们可能难以捕捉关系数据中一些无法轻易建模的重要属性,这些属性通常是结构化的、离散的和符号化的,而简单的向量嵌入仅设计用于捕捉相似性。图1.2展示了这些离散属性的一些示例。我们详细说明如下:
结构模式。关系数据展示了高度复杂的结构模式,如层次结构和循环。典型示例包括描述词义层次的WordNet [120] 和描述基因功能层次的Gene Ontology [5]。基于欧几里得的纯向量嵌入设计用于平面数据,但在建模具有复杂结构模式的数据时表现不佳。例如,层次结构中的节点数量呈指数增长,而欧几里得空间的体积仅相对于半径呈线性增长。
关系/逻辑模式。多关系数据或知识图谱描述了实体之间的关系事实。这些关系展示了许多关系或逻辑模式,如对称性(例如,有朋友)、反转性(是某导演和被某导演)以及蕴含性(例如,某人的母亲→某人的父母)。对这些关系或逻辑模式的建模对于嵌入来说至关重要,不仅可以提高知识图谱嵌入模型的表达能力,更重要的是,促进了保证泛化能力的推理,即一旦学习到这些模式,就可以推断出符合这些模式的事实。
逻辑/集合理论结构。关系数据可以通过应用集合论运算符(如集合包含和集合排除)或逻辑运算符(如逻辑交集和否定)来定义。这对于描述概念/框架知识尤为有用。在这种意义上,概念知识被描述为形式化描述逻辑语言中的逻辑陈述。将描述逻辑中表达的逻辑结构嵌入到嵌入空间中具有挑战性,因为这些逻辑结构需要在嵌入空间中保留,而这超出了纯向量嵌入中相似性的范畴。此外,关系数据中的逻辑结构还可以用于描述机器学习模型输出的关系约束。嵌入这些约束对于许多多标签机器学习模型至关重要,因为它可以保证预测的一致性。
高阶结构。关系数据可能描述了高阶关系事实,每个事实可以描述多个实体和/或关系之间的复杂多重关系。例如,在超关系或n元关系知识图谱中,每个三元事实通过一组限定符来进行上下文化,每个限定符是一个关系-实体对。另一个例子是嵌套的关系知识图谱,其中一个事实可以描述关于其他事实的关系,也就是“事实上的事实”。大多数知识图谱嵌入方法是为基于三元组的知识图谱设计的,难以捕捉高阶知识。对这些高阶知识的建模具有挑战性,因为逻辑属性不仅可能存在于三元组层面,还可能存在于高阶结构层面。例如,在查询超关系事实时,向一个事实附加限定符只会缩小答案集,而不会扩大它,即限定符单调性。在嵌套关系知识图谱中,嵌套的关系事实可能表达某些逻辑规则。
超越纯向量嵌入,几何关系嵌入将纯向量表示替换为更高级的几何对象,如凸区域 [98, 144]、概率密度函数 [145, 175]、非欧几里得流形上的几何元素 [26] 及其组合 [161]。不同于纯向量嵌入,几何关系嵌入为建模关系数据的各种离散属性提供了丰富的几何归纳偏置,同时仍能够捕捉相似性。例如,将本体概念嵌入为凸区域不仅可以建模概念的相似性,还可以建模概念上的集合运算和逻辑运算,如集合包含、集合交集 [199] 和逻辑否定 [215]。这对于本体中的概念嵌入非常有用。另一方面,将数据表示在非欧几里得黎曼流形上可以捕捉复杂的结构模式,如在双曲空间中表示层次结构 [26] 和在球面空间中表示循环。几何关系嵌入已成功应用于许多关系推理任务中,包括但不限于知识图谱(KG)补全 [1]、本体/层次推理 [171]、层次多标签分类 [139] 和逻辑查询回答 [145]。然而,不同的下游应用对底层嵌入的能力要求不同,因此需要对嵌入的特征和任务要求有充分的理解,才能做出适当的选择。
1.2 研究问题
我们探讨以下研究问题(RQs): RQ 1:如何在图数据中准确建模复杂的图结构模式,如层次结构和循环?这些结构模式适合什么样的几何归纳偏置?如何开发适合建模这些结构模式的图神经网络组件?(第3.1章) RQ 2:对于同时呈现复杂图结构模式(如层次结构和循环)和复杂关系模式(如对称性、反对称性、反转性和组成性)的多关系图或知识图,如何在单一嵌入空间中准确建模这两种模式?(第3.2章) RQ 3:对于以描述逻辑语言表达的逻辑陈述/公理的本体数据,如何在保留其逻辑结构的同时,准确表示这些逻辑陈述/公理?用于表示概念的几何归纳偏置是什么?(第4章) RQ 4:如何表示机器学习模型的关系约束,以便模型可以生成符合这些关系约束的逻辑一致性输出?(第5章) RQ 5:如何嵌入具有高阶关系结构的关系数据,如超关系知识图谱和嵌套关系知识图谱,同时确保这些数据中固有的逻辑模式得到准确建模?(第6章) 为了解决这些限制,本论文超越了向量嵌入,提出了多种几何嵌入方法,以准确建模不同类型关系数据的各种离散属性。几何嵌入不是将关系对象映射为欧几里得空间中的简单向量,而是将其编码为几何元素(例如球体、盒子和凸锥)或非欧几里得流形中的元素(例如双曲或球面空间)。几何嵌入的主要优势在于能够准确编码关系数据的离散属性。在本论文中,我们使用几何嵌入解决了关系数据向量嵌入中的若干编码问题(参见图1.3)。我们所做的贡献和论文的其余内容总结如下: * 在第2章,我们介绍了一些相关的预备知识、基础概念和相关工作。 * 在第3章,我们介绍了伪黎曼流形嵌入。本章有以下两项贡献:
我们提出了一个原则性框架,即伪黎曼GCN,它将GCN推广到具有不定度量的伪黎曼流形,提供了更灵活的归纳偏置以适应具有混合拓扑结构的复杂图形。我们还通过新颖的测地线工具定义了伪黎曼流形中的神经网络操作,以促进伪黎曼几何在几何深度学习中的应用。通过对三个标准任务的广泛评估表明,我们的模型在黎曼流形上的基线模型中表现更优。 * 我们提出了UltraE,一种在伪黎曼流形中交织使用双曲几何和球面几何的超双曲知识图谱嵌入方法。该方法允许同时建模知识图谱中的多层次和非层次结构。我们通过伪正交变换导出关系嵌入,该变换分解为包括圆形旋转/反射和双曲旋转在内的各种几何运算,从而推断知识图谱中的复杂关系模式。在三个标准知识图谱数据集上,UltraE在低维设置下优于许多先前的欧几里得和非欧几里得模型。 * 在第4章,我们专注于本体嵌入,做出了以下贡献:
我们提出了BoxEL,一种几何知识库嵌入方法,能够显式建模由EL++理论表达的逻辑结构。与忽略分析保证的标准知识图谱嵌入方法不同,BoxEL通过将背景知识整合到机器学习任务中,提供了底层逻辑结构的可靠性保证,从而为知识库推理提供了一种更加可靠且保留逻辑的方式。实验证明,BoxEL在三个本体上的包含推理和预测真实世界生物医学知识库中的蛋白质相互作用方面优于以往的知识图谱嵌入和EL++嵌入方法。 * 在第5章,我们研究了本体嵌入在提高机器学习模型中的作用,并做出了以下贡献:
我们专注于一个结构化多标签预测任务,其输出应遵守蕴含和排除约束。我们展示了这个问题可以在双曲Poincaré球空间中被表述,其中线性决策边界(Poincaré超平面)可以解释为凸区域。蕴含和排除约束在几何上分别被解释为内部性和分离性。在12个数据集上的实验显示,模型在平均精度和约束违规减少方面有显著改进,即使在维度比基线减少了一个数量级的情况下。 * 在第6章,我们引入了两个用于高阶关系知识图谱的几何嵌入方法:
我们提出了ShrinkE,一种几何超关系知识图谱嵌入方法,旨在显式建模这些模式。ShrinkE通过从头实体到关系特定的盒子的空间功能转换来建模主要三元组。每个限定符“收缩”盒子以缩小可能的答案集,从而实现限定符的单调性。限定符盒子之间的空间关系允许建模限定符的核心推理模式,如蕴含和互斥。实验结果表明,ShrinkE在三个超关系知识图谱的基准上表现优异。 * 我们提出了FactE,这是一系列超复数嵌入方法,能够嵌入原子和嵌套事实知识。该框架有效捕捉了由嵌套事实中出现的逻辑模式。实验证明,FactE在性能上相比现有基线方法有显著提升。此外,我们的广义超复数嵌入框架统一了先前的代数(如四元数)和几何(如双曲几何)嵌入方法,提供了嵌入多种关系类型的多功能性。 * 在第7章,我们总结了整篇论文,归纳了局限性,并展望了未来的研究方向。
本论文包含一些已在会议论文集中发表的材料,如下所列。除非特别说明,这些论文的创意生成、实验和论文写作等方面均由作者主要贡献。