【普林斯顿博士论文】大规模模型的迁移学习与优化理论

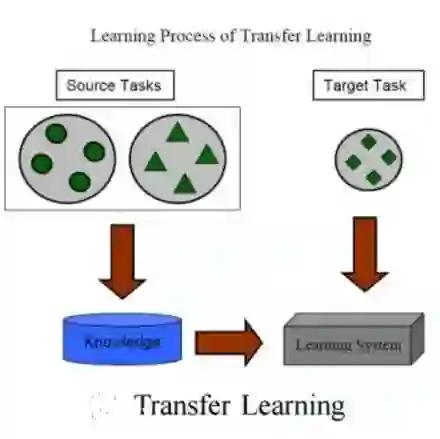
近年来，随着迁移学习和基于梯度的优化在机器学习各个领域取得成功，理论保证的研究兴趣激增。本论文讨论了在大规模机器学习模型中，统计迁移学习和优化收敛性面临的若干关键挑战。 在第二章中，我们解决了由于贝叶斯分类器中的模糊性以及目标和源分布之间的弱迁移信号而带来的稳健迁移学习挑战。我们引入了“模糊性水平”这一新颖的度量标准，用于衡量目标和源回归函数之间的差异，提出了一种简单的迁移学习过程，并给出了一个将该量与风险改进相关联的通用定理。通过非参数分类和逻辑回归任务，我们验证了该方法的有效性。 在第三章中，我们为高维非参数回归中的深度ReLU神经网络迁移学习（或微调）提出了一个统一的框架，同时处理协变量和后验分布的变化。通过使用具有稀疏低维非参数交互的潜变量模型，我们证明了我们提出的微调因子增强方法能够实现最优的统计收敛速率，能够适应目标和源回归函数的未知低维结构。此外，我们提出了一种基于模型选择的多样化投影过程，通过利用额外的源数据，提供了对潜变量空间的更鲁棒估计。 在第四章中，我们分析了在训练Transformer模型时，带权重衰减正则化的梯度流的收敛性。我们首先建立了大规模Transformer的均值场极限，表明随着模型宽度和深度的增加，梯度流收敛到Wasserstein梯度流，且可以用偏微分方程（PDE）表示。接着，我们证明了当权重衰减较小时，梯度流能够达到与PDE解一致的全局最小值。 https://dataspace.princeton.edu/handle/88435/dsp01cn69m7532机器学习因其广泛的应用范围和适应性技术的快速发展而获得了巨大的关注。在大语言模型的时代，这一趋势得到了进一步的放大，大语言模型突破了深度模型的可扩展性限制，推动了新方法的发展，这些方法在不同任务中表现出色。有两个关键观察值得注意：• 迁移学习的需求：首先，迁移学习——通常在计算机科学领域以微调（fine-tuning）框架进行研究——已经变得广泛应用，因为从头开始重新训练庞大的模型通常由于计算资源的限制而不可行。这个研究领域涉及的任务是，训练数据来自与我们需要做出预测的目标数据分布相似，但并不完全相同的分布。除了节省计算资源，迁移学习的目标是将源领域的知识迁移到目标数据上，从而增强学习效果，通常通过在源数据上构建的预训练模型实现。• 大规模模型训练的挑战：其次，尽管深度模型——特别是在大语言模型时代的Transformer大规模模型——以及迁移学习等技术得到了广泛应用，但我们对这些模型的优化保证的理解仍处于初步阶段。一个显著的观察是，随着模型规模的增加，基于梯度的训练方法通常能够在训练目标函数的高度非凸景观下成功地实现极低的训练损失。尤其是在训练大规模Transformer模型时，如何保证这些方法的稳定性和有效性，仍然是一个难解的问题。尽管大规模模型如神经网络和Transformer已经展示了显著的经验成功，但仍缺乏对一系列广泛使用的训练方法（如迁移学习和优化属性）的严格理论保证。因此，填补这些现代技术在实践成功与理论基础之间的鸿沟，成为了一个关键挑战，亟需开发新的、稳健的方法论。为此，本论文提出了旨在从理论上严谨地解决这些挑战的方法。具体来说，我研究了在源数据不可靠的情况下，稳健迁移学习的问题，针对深度ReLU神经网络在非参数回归中的迁移学习问题，以及通过梯度流训练Transformer模型的全局收敛性保证。每个问题都针对高维情况，采用大规模模型作为解决方法。在本章的后续部分，我将概述本文的主要贡献。