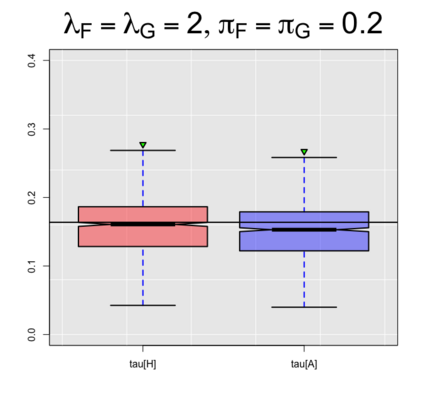
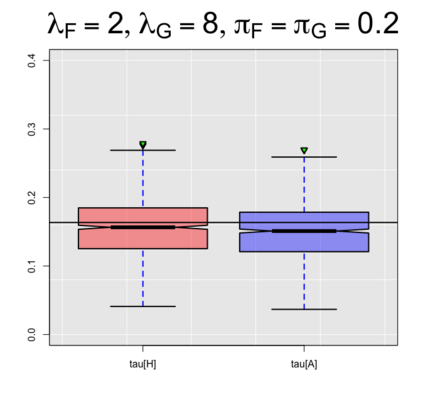
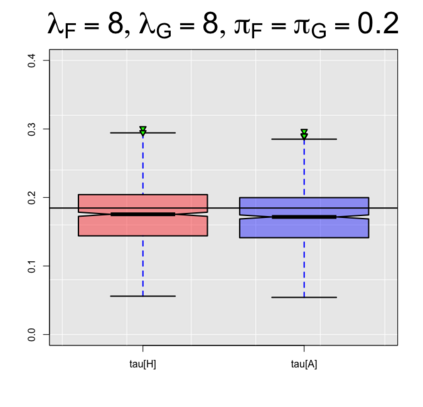
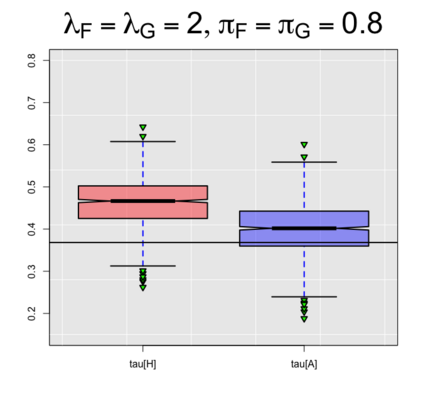
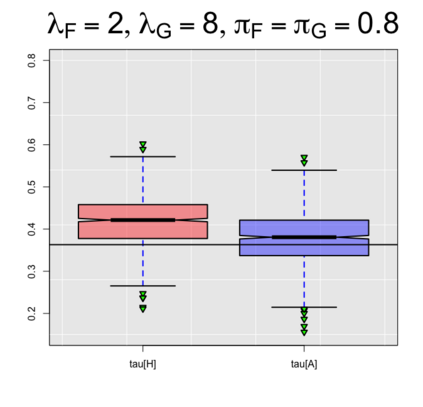
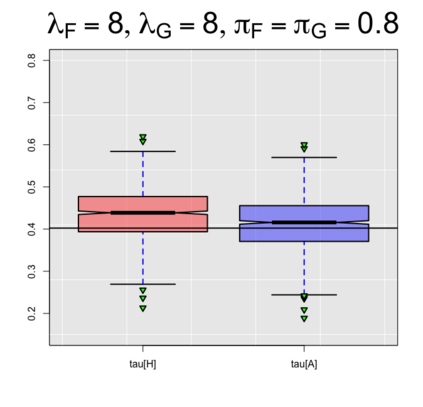
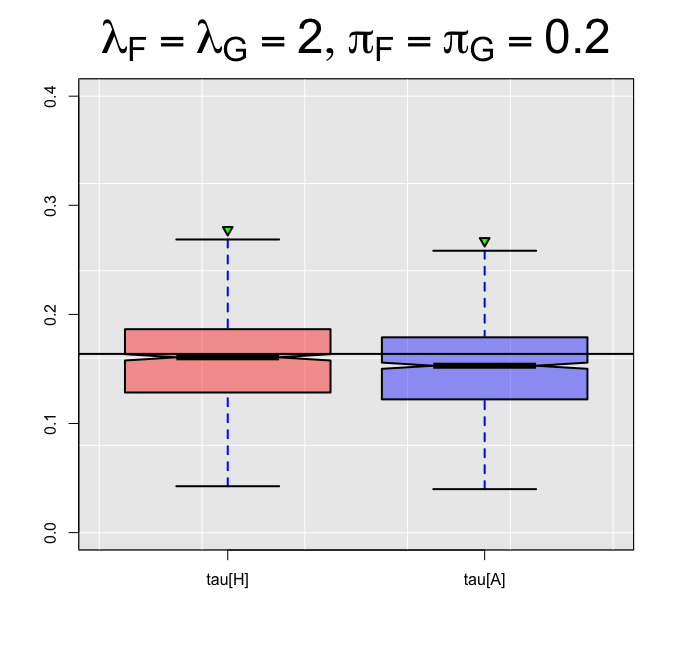
In this paper, we extend the work of Pimentel et al. (2015) and propose an adjusted estimator of Kendall's $\tau$ for bivariate zero-inflated count data. We provide achievable lower and upper bounds of our proposed estimator and show its relationship with current literature. In addition, we also suggest an estimator of the achievable bounds, thereby helping practitioners interpret the results while working with real data. The performance of the proposed estimator for Kendall's $\tau$ is unbiased with smaller mean squared errors compared to the unadjusted estimator of Pimentel et al. (2015). Our results also show that the bound estimator can be used when knowledge of the marginal distributions is lacking.
翻译:在本文中,我们扩展了Pimentel等人(2015年)的工作,并提议调整Kendall $\tau$的估算值,用于计算双轨零膨胀计数数据。我们提供了我们提议的估算值的下限和上限,并展示了与当前文献的关系。此外,我们还建议对可实现界限的估算值,从而帮助从业者在使用真实数据的同时解释结果。 Kendall $\tau$的拟议估算值的表现是不带偏见的,与Pimentel et al(2015年)未调整的估算值相比,其平均正方差较小。我们的结果还表明,当对边际分布缺乏了解时,可使用边际估计值。