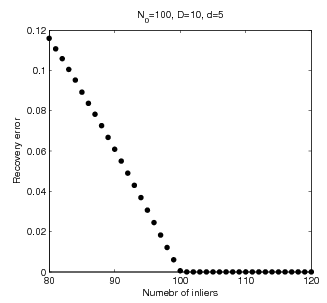
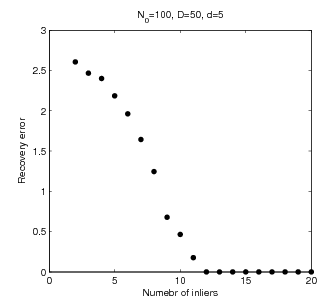
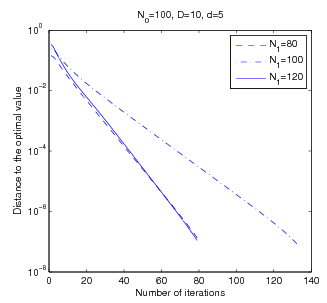
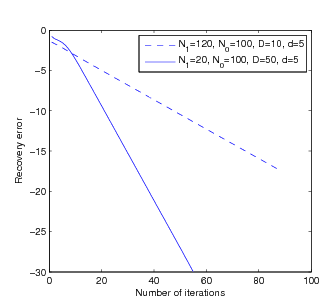
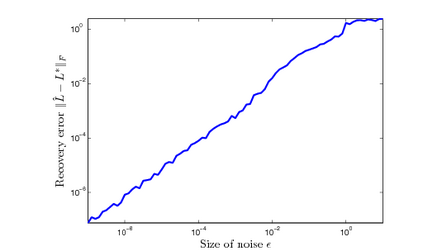
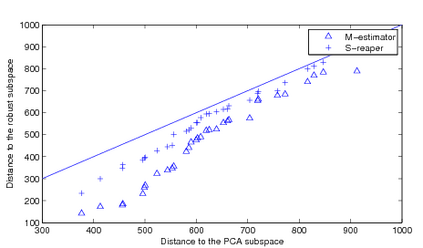
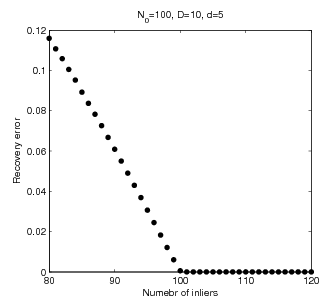
This paper considers the problem of robust subspace recovery: given a set of $N$ points in $\mathbb{R}^D$, if many lie in a $d$-dimensional subspace, then can we recover the underlying subspace? We show that Tyler's M-estimator can be used to recover the underlying subspace, if the percentage of the inliers is larger than $d/D$ and the data points lie in general position. Empirically, Tyler's M-estimator compares favorably with other convex subspace recovery algorithms in both simulations and experiments on real data sets.
翻译:本文考虑了稳健的子空间回收问题:考虑到一套以$\mathbb{R ⁇ D$计的美元点数,如果有许多位于一个以美元为维的子空间中,那么我们能否收回基础的子空间?我们证明,如果离子的百分比大于美元/美元,而数据点处于一般位置,那么,泰勒的M-估计值与其他在模拟和实验真实数据集中的convex次空间回收算法相比,都比较优于其他 convex次空间回收算法。
相关内容
专知会员服务
158+阅读 · 2020年1月29日
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2021年6月18日
Arxiv
0+阅读 · 2021年6月16日